Lente (óptica)
Definición
Una lente es un dispositivo óptico transmisivo que enfoca o dispersa un haz de luz por medio de la refracción. Una lente simple consiste en una sola pieza de material transparente, mientras que una lente compuesta consiste en varias lentes simples ( elementos ), generalmente dispuestas a lo largo de un eje común. Las lentes están hechas de materiales como vidrio o plástico, y se muelen y pulimentan o moldean a la forma deseada. Una lente puede enfocar la luz para formar una imagen, a diferencia de un prisma, que refracta la luz sin enfocar. Los dispositivos que de manera similar enfocan o dispersan las ondas y la radiación además de la luz visible también se llaman lentes, como lentes de microondas, lentes de electrones, lentes acústicas o lentes explosivas.
Historia
La palabra lente proviene de lēns , el nombre latino de la lenteja, porque una lente doble convexa tiene forma de lenteja. La planta de lentejas también le da su nombre a una figura geométrica.
Algunos estudiosos sostienen que la evidencia arqueológica indica que hubo un uso generalizado de lentes en la antigüedad, que abarca varios milenios. La llamada lente Nimrud es un artefacto de cristal de roca del siglo VII a. C. que puede o no haber sido utilizado como una lupa o como un vaso ardiente. Otros han sugerido que ciertos jeroglíficos egipcios representan "lentes meniscales de vidrio simples".
La referencia cierta más antigua al uso de lentes es de la obra de Aristófanes The Clouds (424 aC) mencionando una copa de fuego. Plinio el Viejo (siglo I) confirma que los vasos ardientes eran conocidos en la época romana. Pliny también tiene la referencia más antigua conocida sobre el uso de una lente correctiva cuando menciona que se dijo que Nero miraba los juegos de gladiadores usando una esmeralda (presumiblemente cóncava para corregir la miopía, aunque la referencia es vaga). Tanto Plinio como Séneca el Joven (3 aC-65 dC) describieron el efecto de aumento de un globo de vidrio lleno de agua.
Ptolomeo (siglo II) escribió un libro sobre Óptica , que sin embargo solo sobrevive en la traducción al latín de una traducción árabe incompleta y muy pobre. El libro, sin embargo, fue recibido por eruditos medievales en el mundo islámico, y comentado por Ibn Sahl (siglo X), quien a su vez fue mejorado por Alhazen ( Libro de Óptica , siglo XI). La palabra árabe para "lente", عدسة' adasa ("lenteja") es una traducción directa de préstamo de lente latina , lentícula . La traducción árabe de la óptica de Ptolomeo se hizo disponible en traducción latina en el siglo XII (Eugenio de Palermo 1154). Entre los siglos XI y XIII se inventaron las "piedras de lectura". Estas fueron lentes primitivas plano-convexas, inicialmente creadas cortando una esfera de vidrio por la mitad. Las lentes Visby de cizallas medievales (siglos XI o XII) pueden o no haber sido diseñadas para usar como anteojos ardientes.
Los espectáculos fueron inventados como una mejora de las "piedras de lectura" de la alta época medieval en el norte de Italia en la segunda mitad del siglo XIII. Este fue el comienzo de la industria óptica de lentes de pulido y amolado para gafas, primero en Venecia y Florencia a fines del siglo XIII, y más tarde en los centros de fabricación de gafas tanto en los Países Bajos como en Alemania. Los creadores de espectáculos crearon tipos mejorados de lentes para la corrección de la visión basados más en el conocimiento empírico obtenido al observar los efectos de las lentes (probablemente sin el conocimiento de la teoría óptica rudimentaria del día). El desarrollo práctico y la experimentación con lentes condujeron a la invención del microscopio óptico compuesto alrededor de 1595, y al telescopio refractor en 1608,
Con la invención del telescopio y el microscopio hubo una gran cantidad de experimentación con formas de lentes en el siglo XVII y principios del siglo XVIII, tratando de corregir los errores cromáticos observados en los lentes. Los ópticos trataron de construir lentes de formas variables de curvatura, asumiendo erróneamente que los errores se debían a defectos en la figura esférica de sus superficies. La teoría óptica sobre la refracción y la experimentación estaba demostrando que ninguna lente de elemento único podría enfocar todos los colores. Esto condujo a la invención de la lente acromática compuesta por Chester Moore Hall en Inglaterra en 1733, una invención también reivindicada por su colega inglés John Dollond en una patente de 1758.
Construcción de lentes simples
La mayoría de las lentes son esféricas : sus dos superficies son partes de las superficies de las esferas. Cada superficie puede ser convexa (abultada hacia afuera desde la lente), cóncava (presionada en la lente) o plana (plana). La línea que une los centros de las esferas que forman las superficies de la lente se denomina eje de la lente. Normalmente, el eje de la lente pasa a través del centro físico de la lente, debido a la forma en que se fabrican. Las lentes se pueden cortar o rectificar después de la fabricación para darles una forma o tamaño diferente. El eje de la lente puede no pasar a través del centro físico de la lente.
Las lentes tóricas o esfero-cilíndricas tienen superficies con dos radios de curvatura diferentes en dos planos ortogonales. Tienen una potencia focal diferente en diferentes meridianos. Esto forma una lente astigmática. Un ejemplo son las gafas que se usan para corregir el astigmatismo en el ojo de otra persona.
Más complejos son los lentes asféricos. Estas son lentes donde una o ambas superficies tienen una forma que no es ni esférica ni cilíndrica. Las formas más complicadas permiten que tales lentes formen imágenes con menos aberración que las lentes simples estándar, pero son más difíciles y caras de producir.
Tipos de lentes simples
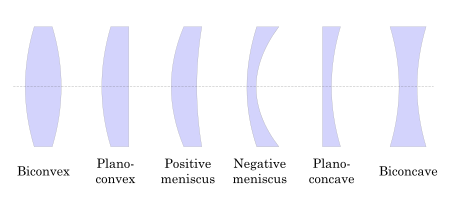
Las lentes se clasifican por la curvatura de las dos superficies ópticas. Una lente es biconvexa (o doblemente convexa , o simplemente convexa ) si ambas superficies son convexas. Si ambas superficies tienen el mismo radio de curvatura, la lente es equiconvexa . Una lente con dos superficies cóncavas es bicóncava (o simplemente cóncava ). Si una de las superficies es plana, la lente es plano-convexa o plano-cóncavasegún la curvatura de la otra superficie. Una lente con un lado convexo y uno cóncavo es convexo-cóncavo o menisco . Este es el tipo de lente que se usa con mayor frecuencia en lentes correctivos.
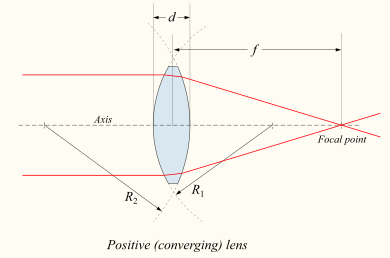
Si la lente es biconvexa o plano-convexa, un haz colimado de luz que pasa a través de la lente converge hacia una mancha (un foco ) detrás de la lente. En este caso, la lente se denomina lente positiva o convergente . La distancia de la lente al punto es la distancia focal de la lente, que comúnmente se abrevia f en diagramas y ecuaciones. Una lente hemisférica extendida es un tipo especial de lente plano-convexa, en la cual la superficie curva de la lente es un hemisferio completo y la lente es mucho más gruesa que el radio de curvatura.
 |  |
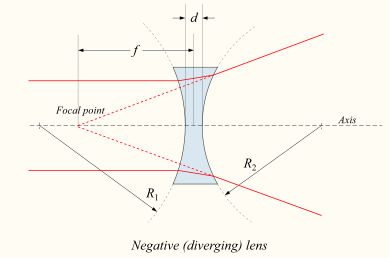
Si la lente es bicóncava o plano-cóncava, un rayo de luz colimado que pasa a través de la lente diverge (se extiende); la lente se denomina lente negativa o divergente . El haz, después de pasar a través de la lente, parece emanar de un punto particular en el eje delante de la lente. La distancia desde este punto a la lente también se conoce como distancia focal, aunque es negativa con respecto a la distancia focal de una lente convergente.
 |  |
Las lentes convexo-cóncavas (menisco) pueden ser positivas o negativas, dependiendo de las curvaturas relativas de las dos superficies. Una lente de menisco negativo tiene una superficie cóncava más pronunciada y es más delgada en el centro que en la periferia. Por el contrario, un lente de menisco positivo tiene una superficie convexa más pronunciada y es más grueso en el centro que en la periferia. Una lente delgada ideal con dos superficies de igual curvatura tendría cero potencia óptica, lo que significa que no convergería ni divergiría de la luz. Sin embargo, todas las lentes reales tienen un espesor distinto de cero, lo que hace que una lente real con superficies curvas idénticas sea ligeramente positiva. Para obtener exactamente la potencia óptica cero, una lente de menisco debe tener curvaturas ligeramente desiguales para tener en cuenta el efecto del grosor de la lente.
Ecuación de Lensmaker
La distancia focal de una lente en el aire se puede calcular a partir de la ecuación del fabricante de la lente :
dónde
- es la distancia focal de la lente,
- es el índice de refracción del material de la lente,
- es el radio de curvatura (con signo, ver debajo) de la superficie de la lente más cerca de la fuente de luz,
- es el radio de curvatura de la superficie de la lente más alejado de la fuente de luz, y
- es el grosor de la lente (la distancia a lo largo del eje de la lente entre los dos vértices de la superficie).
La distancia focal f es positiva para lentes convergentes y negativa para lentes divergentes. El recíproco de la distancia focal, 1 / f , es la potencia óptica de la lente. Si la distancia focal está en metros, esto proporciona la potencia óptica en dioptrías (metros inversos).
Las lentes tienen la misma distancia focal cuando la luz viaja de atrás hacia adelante como cuando la luz va de adelante hacia atrás. Otras propiedades de la lente, como las aberraciones, no son las mismas en ambas direcciones.
Convenio de signos para radios de curvatura R 1 y R 2
Los signos de los radios de curvatura de la lente indican si las superficies correspondientes son convexas o cóncavas. La convención de signos utilizada para representar esto varía, pero en este artículo una R positiva indica que el centro de curvatura de la superficie está más adelante en la dirección del recorrido del rayo (derecha, en los diagramas acompañantes), mientras que R negativa significa que los rayos alcanzan la superficie ya han pasado el centro de curvatura. En consecuencia, para superficies de lentes externas como se diagrama anteriormente, R 1 > 0 y R 2 <0 indican superficies convexas (usadas para converger la luz en una lente positiva), mientras que R 1 <0 y R 2 > 0 indican superficies cóncavas . El recíproco del radio de curvatura se llama curvatura. Una superficie plana tiene curvatura cero, y su radio de curvatura es infinito.
Aproximación de lente delgada
Si d es pequeño en comparación con R 1 y R 2 , entonces se puede hacer la aproximación de lente delgada . Para una lente en el aire, f es dada por
Propiedades de imagen
Como se mencionó anteriormente, una lente positiva o convergente en el aire enfoca un haz colimado que viaja a lo largo del eje de la lente a una mancha (conocida como punto focal) a una distancia f de la lente. Por el contrario, una fuente puntual de luz colocada en el punto focal se convierte en un haz colimado por la lente. Estos dos casos son ejemplos de formación de imágenes en lentes. En el primer caso, un objeto a una distancia infinita (representado por un haz colimado de ondas) se enfoca a una imagen en el punto focal de la lente. En este último, un objeto a la distancia de distancia focal de la lente se representa con imágenes al infinito. El plano perpendicular al eje de la lente situado a una distancia f de la lente se denomina plano focal .
Si las distancias desde el objeto a la lente y desde la lente a la imagen son S 1 y S 2 , respectivamente, para una lente de grosor insignificante, en el aire, las distancias están relacionadas por la fórmula de la lente delgada :
- .
Esto también se puede poner en la forma "newtoniana":
donde y .
Por lo tanto, si un objeto se coloca a una distancia S 1 > f de un lente positivo de distancia focal f , encontraremos una distancia de imagen S 2 de acuerdo con esta fórmula. Si se coloca una pantalla a una distancia S 2 en el lado opuesto de la lente, se forma una imagen sobre ella. Este tipo de imagen, que se puede proyectar en una pantalla o sensor de imagen, se conoce como una imagen real .
Este es el principio de la cámara y del ojo humano. El ajuste de enfoque de una cámara ajusta S 2 , ya que el uso de una distancia de imagen diferente a la requerida por esta fórmula produce una imagen desenfocada (borrosa) para un objeto a una distancia de S 1 de la cámara. Dicho de otra manera, modificar S 2 hace que los objetos en un S 1 diferente entren en el foco perfecto.
En algunos casos, S 2 es negativo, lo que indica que la imagen se forma en el lado opuesto de la lente desde donde se consideran esos rayos. Dado que los rayos de luz divergentes que emanan de la lente nunca entran en el foco, y esos rayos no están presentes físicamente en el punto donde parecen formar una imagen, esto se llama imagen virtual. A diferencia de las imágenes reales, una imagen virtual no se puede proyectar en una pantalla, sino que aparece para un observador que mira a través de la lente como si fuera un objeto real en la ubicación de esa imagen virtual. Del mismo modo, una lente posterior parece como si fuera un objeto en esa ubicación, de modo que la segunda lente podría volver a enfocar esa luz en una imagen real, S 1 luego se mide desde la ubicación de la imagen virtual detrás de la primera lente hasta la segunda lente. Esto es exactamente lo que hace el ojo cuando mira a través de una lupa. La lupa crea una imagen virtual (magnificada) detrás de la lupa, pero esos rayos son luego reimpresos por la lente del ojo para crear una imagen real en la retina.
Usando una lente positiva de distancia focal f, una imagen virtual resulta cuando S 1 < f , la lente se usa como lupa (en lugar de S 1 >> f como para una cámara). El uso de una lente negativa ( f <0 ) con un objeto real ( S 1 > 0 ) solo puede producir una imagen virtual ( S 2 <0 ), de acuerdo con la fórmula anterior. También es posible para la distancia del objeto S 1 a ser negativo, en cuyo caso la lente ve una llamada objeto virtual. Esto ocurre cuando la lente se inserta en un haz convergente (enfocado por una lente anterior) antes de la ubicación de su imagen real. En ese caso, incluso una lente negativa puede proyectar una imagen real, como lo hace una lente Barlow.
Para una lente delgada, las distancias S 1 y S 2 se miden desde el objeto y la imagen a la posición de la lente, como se describió anteriormente. Cuando el grosor de la lente no es mucho más pequeño que S 1 y S 2 o hay múltiples elementos de lente (una lente compuesta), uno debe en cambio medir desde el objeto y la imagen hasta los planos principales de la lente. Si las distancias S 1 o S 2 pasan a través de un medio diferente al aire o al vacío, se requiere un análisis más complicado.
Aumento
La ampliación lineal de un sistema de imágenes con una sola lente viene dada por
- ,
donde M es el factor de ampliación definido como la relación entre el tamaño de una imagen y el tamaño del objeto. La convención de signos aquí dicta que si M es negativo, como lo es para imágenes reales, la imagen está boca abajo con respecto al objeto. Para imágenes virtuales, M es positivo, por lo que la imagen es vertical.
La ampliación lineal M no siempre es la medida más útil de potencia de aumento. Por ejemplo, al caracterizar un telescopio visual o binoculares que producen solo una imagen virtual, uno estaría más interesado en la ampliación angular, que expresa cuánto más grande aparece un objeto distante a través del telescopio en comparación con el ojo desnudo. En el caso de una cámara, se podría citar la escala de la placa, que compara el tamaño aparente (angular) de un objeto distante con el tamaño de la imagen real producida en el foco. La escala de la placa es el recíproco de la distancia focal de la lente de la cámara; Las lentes se clasifican como lentes de foco largo o lentes gran angular de acuerdo con sus distancias focales.
Usar una medición inadecuada de aumento puede ser formalmente correcto pero producir un número sin sentido. Por ejemplo, usando una lupa de 5 cm de distancia focal, sostenida a 20 cm del ojo y a 5 cm del objeto, produce una imagen virtual en infinito de tamaño infinito: M = ∞ . Pero la ampliación angular es 5, lo que significa que el objeto aparece 5 veces más grande para el ojo que sin la lente. Al tomar una foto de la luna usando una cámara con una lente de 50 mm, a uno no le preocupa la ampliación lineal M ≈ -50 mm / 380 000 km = -1.3 × 10 .Más bien, la escala de la placa de la cámara es de aproximadamente 1 ° / mm, de lo que se puede concluir que la imagen de 0,5 mm en la película corresponde a un tamaño angular de la luna visto desde la tierra de aproximadamente 0,5 °.
En el caso extremo en que un objeto es una distancia infinita, S 1 = ∞ , S 2 = f y M = - f / ∞ = 0 , lo que indica que el objeto se obtuvieron imágenes a un único punto en el plano focal. De hecho, el diámetro del punto proyectado no es en realidad cero, ya que la difracción coloca un límite inferior en el tamaño de la función de dispersión de puntos. Esto se llama límite de difracción.
Aberraciones
| Aberración óptica |
|---|
Las lentes no forman imágenes perfectas, y una lente siempre presenta cierto grado de distorsión o aberración que hace que la imagen sea una réplica imperfecta del objeto. El diseño cuidadoso del sistema de lentes para una aplicación particular minimiza la aberración. Varios tipos de aberración afectan la calidad de la imagen, incluida la aberración esférica, el coma y la aberración cromática.
Aberración esférica
La aberración esférica se produce porque las superficies esféricas no son la forma ideal para una lente, pero son con diferencia la forma más simple a la que se puede pulir y pulir el vidrio, y así se usan a menudo. La aberración esférica hace que los haces paralelos al eje de la lente se enfoquen en un lugar ligeramente diferente de los que se encuentran cerca del eje. Esto se manifiesta como una borrosidad de la imagen. Las lentes en las que se usan superficies no esféricas más cercanas a las ideales se llaman asféricas lentes. Anteriormente eran complejos de hacer y, a menudo, extremadamente caros, pero los avances en la tecnología han reducido en gran medida el costo de fabricación de tales lentes. La aberración esférica se puede minimizar eligiendo cuidadosamente las curvaturas de la superficie para una aplicación en particular. Por ejemplo, una lente plano-convexa, que se usa para enfocar un haz colimado, produce un punto focal más agudo cuando se usa con el lado convexo hacia la fuente del haz.

Coma
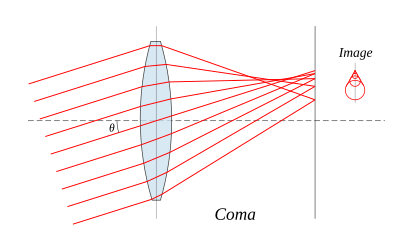
Coma , o aberración comática , deriva su nombre de la apariencia de cometa de la imagen aberrada. El coma ocurre cuando se toma una imagen de un objeto fuera del eje óptico de la lente, donde los rayos pasan a través de la lente formando un ángulo con el eje θ. Los rayos que pasan por el centro de una lente de distancia focal f se enfocan en un punto con distancia f tan θ desde el eje. Los rayos que pasan a través de los márgenes externos de la lente se enfocan en diferentes puntos, ya sea más lejos del eje (coma positivo) o más cerca del eje (coma negativo). En general, un haz de rayos paralelos que pasa a través de la lente a una distancia fija desde el centro de la lente se enfoca a una imagen en forma de anillo en el plano focal, conocido como un círculo comático. La suma de todos estos círculos da como resultado una llamarada en forma de V o de cometa. Al igual que con la aberración esférica, el coma se puede minimizar (y en algunos casos eliminar) eligiendo la curvatura de las dos superficies de la lente para que coincida con la aplicación. Objetivos, en el que se reducen al mínimo tanto la aberración esférica y coma se llaman Bestform lentes.
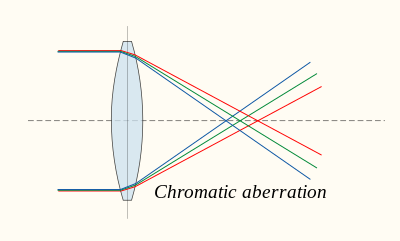
Aberración cromática
La aberración cromática es causada por la dispersión del material de la lente, la variación de su índice de refracción, n , con la longitud de onda de la luz. Dado que, a partir de las fórmulas anteriores, f depende de n , se deduce que la luz de diferentes longitudes de onda se enfoca a diferentes posiciones. La aberración cromática de una lente se ve como franjas de color alrededor de la imagen. Se puede minimizar usando un doblete acromático (o achromat)) en el que dos materiales con diferentes dispersiones se unen para formar una sola lente. Esto reduce la cantidad de aberración cromática en un cierto rango de longitudes de onda, aunque no produce una corrección perfecta. El uso de acromas fue un paso importante en el desarrollo del microscopio óptico. Un apocromático es un sistema de lentes o lentes con una corrección de la aberración cromática aún mejor, combinado con una corrección mejorada de la aberración esférica. Los apocromatos son mucho más caros que los acromatos.
También se pueden usar diferentes materiales para lentes para minimizar la aberración cromática, tales como revestimientos especializados o lentes hechos de cristal fluorita. Esta sustancia natural tiene el mayor número conocido de Abbe, lo que indica que el material tiene baja dispersión.

Otros tipos de aberración
Otros tipos de aberración incluyen curvatura de campo , distorsión de barril y acerico y astigmatismo .
Difracción de la abertura
Incluso si una lente está diseñada para minimizar o eliminar las aberraciones descritas anteriormente, la calidad de la imagen sigue estando limitada por la difracción de la luz que pasa a través de la apertura finita de la lente. Una lente de difracción limitada es aquella en la que las aberraciones se han reducido hasta el punto en que la calidad de la imagen está limitada principalmente por la difracción en las condiciones de diseño.
Lentes compuestos
Las lentes simples están sujetas a las aberraciones ópticas discutidas anteriormente. En muchos casos, estas aberraciones se pueden compensar en gran medida mediante el uso de una combinación de lentes simples con aberraciones complementarias. Una lente compuesta es una colección de lentes simples de diferentes formas y hechas de materiales de diferentes índices de refracción, dispuestos uno después del otro con un eje común.
El caso más simple es donde las lentes se colocan en contacto: si las lentes de las distancias focales f 1 y f 2 son "delgadas", la longitud focal combinada f de las lentes está dada por
Como 1 / f es la potencia de una lente, se puede ver que las potencias de las lentes delgadas en contacto son aditivas.
Si dos lentes delgadas se separan en el aire a cierta distancia d , la distancia focal para el sistema combinado está dada por
La distancia desde el punto focal frontal de las lentes combinadas a la primera lente se denomina longitud focal frontal (FFL):
Del mismo modo, la distancia desde la segunda lente al punto focal posterior del sistema combinado es la distancia focal posterior (BFL):
Como d tiende a cero, las distancias focales tienden al valor de f dado para las lentes delgadas en contacto.
Si la distancia de separación es igual a la suma de las distancias focales ( d = f 1 + f 2 ), el FFL y el BFL son infinitos. Esto corresponde a un par de lentes que transforman un haz paralelo (colimado) en otro haz colimado. Este tipo de sistema se denomina sistema afocal , ya que no produce convergencia neta o divergencia del haz. Dos lentes en esta separación forman el tipo más simple de telescopio óptico. Aunque el sistema no altera la divergencia de un haz colimado, sí altera el ancho del haz. La ampliación de dicho telescopio viene dada por
que es la relación entre el ancho del haz de salida y el ancho del haz de entrada. Tenga en cuenta la convención de signos: un telescopio con dos lentes convexos ( f 1 > 0, f 2 > 0) produce un aumento negativo, lo que indica una imagen invertida. Una lente convexa más cóncava ( f 1 > 0> f 2 ) produce un aumento positivo y la imagen está en posición vertical. Para obtener más información sobre los telescopios ópticos simples, consulte Refracción del telescopio § Diseños de refracción del telescopio.
Otros tipos
Las lentes cilíndricas tienen curvatura en una sola dirección. Se usan para enfocar la luz en una línea, o para convertir la luz elíptica de un diodo láser en una viga redonda. También se usan en lentes anamórficas con película.
Una lente Fresnel tiene su superficie óptica dividida en anillos estrechos, lo que permite que la lente sea mucho más delgada y ligera que las lentes convencionales. Las lentes de Fresnel duraderas se pueden moldear de plástico y son económicas.
Los lentes lenticulares son matrices de microlentes que se utilizan en la impresión lenticular para crear imágenes que tienen una ilusión de profundidad o que cambian cuando se observan desde diferentes ángulos.
Una lente con índice de gradiente tiene superficies ópticas planas, pero tiene una variación radial o axial en el índice de refracción que hace que la luz que pasa a través de la lente se enfoque.
Un axicon tiene una superficie óptica cónica. Dibuja una fuente puntual en una línea a lo largo del eje óptico o transforma un rayo láser en un anillo.
Los elementos ópticos difractivos pueden funcionar como lentes.
Las superlentes están hechas de metamateriales de índice negativo y pretenden producir imágenes a resoluciones espaciales superiores al límite de difracción. Los primeros superlentes se hicieron en 2004 utilizando un metamaterial para microondas. Algunos investigadores han mejorado las versiones. A partir de 2014, los superlentes todavía no se han demostrado en longitudes de onda visibles o cercanas al infrarrojo.
Se ha desarrollado un prototipo de lente plana ultrafina, sin curvatura.
Usos
Una sola lente convexa montada en un marco con un mango o soporte es una lupa.
Las lentes se usan como prótesis para la corrección de deficiencias visuales como miopía, hipermetropía, presbicia y astigmatismo. (Consulte lentes correctoras, lentes de contacto, anteojos). La mayoría de las lentes utilizadas para otros propósitos tienen una estricta simetría axial; los lentes de gafas son solo aproximadamente simétricos. Por lo general, se les da forma para que quepan en un marco aproximadamente ovalado, no circular; los centros ópticos se colocan sobre los globos oculares; su curvatura puede no ser axialmente simétrica para corregir el astigmatismo. Las lentes de las gafas de sol están diseñadas para atenuar la luz; lentes de gafas de sol que también corrigen impedimentos visuales pueden ser hechos a medida.
Otros usos son en sistemas de imágenes como monoculares, binoculares, telescopios, microscopios, cámaras y proyectores. Algunos de estos instrumentos producen una imagen virtual cuando se aplican al ojo humano; otros producen una imagen real que se puede capturar en una película fotográfica o un sensor óptico, o se puede ver en una pantalla. En estos dispositivos, las lentes a veces se combinan con espejos curvos para crear un sistema catadióptrico donde la aberración esférica de la lente corrige la aberración opuesta en el espejo (como Schmidt y los correctores de menisco).
Las lentes convexas producen una imagen de un objeto en el infinito en su foco; si se toma la imagen del sol, gran parte de la luz visible e infrarroja incidente en la lente se concentra en la imagen pequeña. Una lente grande crea suficiente intensidad para quemar un objeto inflamable en el punto focal. Dado que la ignición se puede lograr incluso con una lente mal hecha, las lentes se han utilizado como lentes de combustión durante al menos 2400 años. Una aplicación moderna es el uso de lentes relativamente grandes para concentrar la energía solar en células fotovoltaicas relativamente pequeñas, cosechando más energía sin la necesidad de utilizar células más grandes y más caras.
Los sistemas de radioastronomía y radar a menudo usan lentes dieléctricas, comúnmente llamadas antenas de lentes para refractar la radiación electromagnética en una antena colectora.
Las lentes pueden rayarse y desgastarse. Los recubrimientos resistentes a la abrasión están disponibles para ayudar a controlar esto.
Obtenido de: https://en.wikipedia.org/wiki/Lens_(optics)

![{\ frac {1} {f}} = (n-1) \ left [{\ frac {1} {R_ {1}}} - {\ frac {1} {R_ {2}}} + {\ frac {(n-1) d} {nR_ {1} R_ {2}}} \ right],](https://wikimedia.org/api/rest_v1/media/math/render/svg/26fb54977c7f965da063dcaded08258c3377f1d9)





![{\ frac {1} {f}} \ approx \ left (n-1 \ right) \ left [{\ fract {1} {R_ {1}}} - {\ frac {1} {R_ {2}} }\derecho].](https://wikimedia.org/api/rest_v1/media/math/render/svg/c633e7b574392e54107881cd2e697e0ba9a68877)

















