Fuerza
Definición
| Fuerza | |
|---|---|
 Las fuerzas se pueden describir como un empujar o tirar de un objeto. Pueden deberse a fenómenos tales como la gravedad, el magnetismo o cualquier cosa que pueda causar la aceleración de una masa. | |
Símbolos comunes | F → , F , F |
| Unidad SI | newton (N) |
Otras unidades | dyne, libra fuerza, poundal, kip |
| En unidades base SI | kg • m / s |
Derivaciones de otras cantidades | F = m a |
| Dimensión | M L T |
La forma original de la segunda ley de Newton establece que la fuerza neta que actúa sobre un objeto es igual a la velocidad a la que su momento cambia con el tiempo. Si la masa del objeto es constante, esta ley implica que la aceleración de un objeto es directamente proporcional a la fuerza neta que actúa sobre el objeto, está en la dirección de la fuerza neta y es inversamente proporcional a la masa del objeto.
Los conceptos relacionados con la fuerza incluyen: empuje, que aumenta la velocidad de un objeto; arrastre, que disminuye la velocidad de un objeto; y torque, que produce cambios en la velocidad de rotación de un objeto. En un cuerpo extendido, cada parte generalmente aplica fuerzas sobre las partes adyacentes; la distribución de tales fuerzas a través del cuerpo es el estrés mecánico interno. Tales esfuerzos mecánicos internos no causan aceleración de ese cuerpo ya que las fuerzas se equilibran entre sí. La presión, la distribución de muchas fuerzas pequeñas aplicadas sobre un área de un cuerpo, es un tipo simple de estrés que, si no se equilibra, puede hacer que el cuerpo acelere. El estrés generalmente causa la deformación de materiales sólidos o fluye en fluidos.
Desarrollo del concepto
Los filósofos en la antigüedad usaron el concepto de fuerza en el estudio de objetos estacionarios y móviles y máquinas simples, pero pensadores como Aristóteles y Arquímedes mantuvieron errores fundamentales en la comprensión de la fuerza. En parte, esto se debió a una comprensión incompleta de la fuerza de fricción a veces no obvia, y una visión consiguientemente inadecuada de la naturaleza del movimiento natural. Un error fundamental fue la creencia de que se requiere una fuerza para mantener el movimiento, incluso a una velocidad constante. La mayoría de los malentendidos previos sobre el movimiento y la fuerza fueron finalmente corregidos por Galileo Galilei y Sir Isaac Newton. Con su visión matemática, Sir Isaac Newton formuló leyes de movimiento que no mejoraron durante casi trescientos años. A principios del siglo XX,
Con conocimientos modernos de la mecánica cuántica y la tecnología que pueden acelerar partículas cercanas a la velocidad de la luz, la física de partículas ha ideado un modelo estándar para describir las fuerzas entre partículas más pequeñas que los átomos. El Modelo Estándar predice que las partículas intercambiadas llamadas bosones gauge son el medio fundamental por el cual las fuerzas se emiten y se absorben. Solo se conocen cuatro interacciones principales: en orden de fuerza decreciente, son: fuertes, electromagnéticas, débiles y gravitacionales. Las observaciones de física de partículas de alta energía realizadas durante las décadas de 1970 y 1980 confirmaron que las fuerzas débiles y electromagnéticas son expresiones de una interacción electrodébil más fundamental.
Conceptos pre-newtonianos
Desde la antigüedad, el concepto de fuerza ha sido reconocido como parte integral del funcionamiento de cada una de las máquinas simples. La ventaja mecánica que ofrece una máquina simple permite que se use menos fuerza a cambio de esa fuerza que actúa a una distancia mayor por la misma cantidad de trabajo. El análisis de las características de las fuerzas finalmente culminó en el trabajo de Arquímedes, que fue especialmente famoso por formular un tratamiento de las fuerzas flotantes inherentes a los fluidos.
Aristóteles proporcionó una discusión filosófica del concepto de una fuerza como parte integral de la cosmología aristotélica. En la visión de Aristóteles, la esfera terrestre contenía cuatro elementos que descansan en diferentes "lugares naturales" en ella. Aristóteles creía que los objetos inmóviles en la Tierra, aquellos compuestos principalmente de los elementos tierra y agua, estaban en su lugar natural en el suelo y que permanecerían de esa manera si se los dejaba solos. Él distinguió entre la tendencia innata de los objetos de encontrar su "lugar natural" (por ejemplo, para que los cuerpos pesados cayeran), lo que condujo al "movimiento natural" y al movimiento no natural o forzado, que requería la aplicación continua de una fuerza. Esta teoría, basada en la experiencia cotidiana de cómo se mueven los objetos, como la aplicación constante de una fuerza necesaria para mantener el carro en movimiento, tuvo problemas conceptuales para explicar el comportamiento de los proyectiles, como el vuelo de flechas. El lugar donde el arquero mueve el proyectil estaba al comienzo del vuelo, y mientras el proyectil navegaba por el aire, ninguna causa eficiente discernible actúa sobre él. Aristóteles era consciente de este problema y propuso que el aire desplazado a través del camino del proyectil lleva el proyectil a su objetivo. Esta explicación exige un continuo como el aire para el cambio de lugar en general. s ruta lleva el proyectil a su objetivo. Esta explicación exige un continuo como el aire para el cambio de lugar en general. s ruta lleva el proyectil a su objetivo. Esta explicación exige un continuo como el aire para el cambio de lugar en general.
La física aristotélica comenzó a enfrentar la crítica en la ciencia medieval, primero por John Philoponus en el siglo VI.
Las deficiencias de la física aristotélica no se corregirían por completo hasta el trabajo de Galileo Galilei en el siglo XVII, influido por la idea tardomedieval de que los objetos en movimiento forzado tenían una fuerza innata de ímpetu. Galileo construyó un experimento en el que las piedras y las balas de cañón se rodaban por una pendiente para refutar la teoría aristotélica del movimiento. Mostró que los cuerpos se aceleraron por la gravedad en una medida que era independiente de su masa y argumentó que los objetos conservan su velocidad a menos que actúe sobre ellos una fuerza, por ejemplo, la fricción.
Mecánica newtoniana
Sir Isaac Newton describió el movimiento de todos los objetos usando los conceptos de inercia y fuerza, y al hacerlo descubrió que obedecían ciertas leyes de conservación. En 1687, Newton publicó su tesis Philosophiæ Naturalis Principia Mathematica . En este trabajo, Newton estableció tres leyes del movimiento que hasta el día de hoy son la forma en que las fuerzas se describen en física.
Primera ley
La Primera Ley del Movimiento de Newton establece que los objetos continúan moviéndose en un estado de velocidad constante a menos que actúe sobre ellos una fuerza neta externa (fuerza resultante). Esta ley es una extensión de la idea de Galileo de que la velocidad constante estaba asociada con la falta de fuerza neta (ver una descripción más detallada de esto a continuación). Newton propuso que cada objeto con masa tiene una inercia innata que funciona como el equilibrio fundamental "estado natural" en lugar de la idea aristotélica del "estado natural de reposo". Es decir, la Primera Ley empírica de Newton contradice la creencia aristotélica intuitiva de que se requiere una fuerza neta para mantener a un objeto en movimiento a velocidad constante. Al hacer que el reposo sea físicamente indistinguible de una velocidad constante distinta de ceroLa Primera Ley de Newton conecta directamente la inercia con el concepto de velocidades relativas. Específicamente, en sistemas donde los objetos se mueven con velocidades diferentes, es imposible determinar qué objeto está "en movimiento" y qué objeto está "en reposo". Las leyes de la física son las mismas en todo marco inercial de referencia, es decir, en todos los marcos relacionados por una transformación galileana.
Por ejemplo, mientras viaja en un vehículo en movimiento a una velocidad constante, las leyes de la física no cambian como resultado de su movimiento. Si una persona que viaja dentro del vehículo arroja una pelota hacia arriba, esa persona observará que sube verticalmente y cae verticalmente y no tiene que aplicar una fuerza en la dirección en que se mueve el vehículo. Otra persona, al observar el paso del vehículo en movimiento, observa que la pelota sigue una trayectoria parabólica curva en la misma dirección que el movimiento del vehículo. Es la inercia de la bola asociada con su velocidad constante en la dirección del movimiento del vehículo lo que asegura que la pelota continúe avanzando incluso cuando se lanza hacia arriba y vuelve a caer. Desde la perspectiva de la persona en el automóvil, el vehículo y todo lo que está dentro de él está en reposo: Es el mundo exterior el que se mueve con una velocidad constante en la dirección opuesta al vehículo. Como no hay ningún experimento que pueda distinguir si es el vehículo que está en reposo o el mundo exterior el que está en reposo, se considera que las dos situaciones son físicamente indistinguibles. La inercia, por lo tanto, se aplica igualmente bien al movimiento de velocidad constante que al reposo.
Segunda ley
Una declaración moderna de la Segunda Ley de Newton es una ecuación vectorial:
dónde está el impulso del sistema, y es la fuerza neta (suma de vectores). Si un cuerpo está en equilibrio, hay una fuerza netacero por definición (sin embargo, pueden existir fuerzas equilibradas). Por el contrario, la segunda ley establece que si hay una fuerza desequilibrada que actúa sobre un objeto, el ímpetu del objeto cambiará con el tiempo.
Por la definición de impulso,
donde m es la masa y es la velocidad.
Si la segunda ley de Newton se aplica a un sistema de masa constante, m puede moverse fuera del operador derivado. La ecuación se convierte en
Al sustituir la definición de aceleración, se deriva la versión algebraica de la Segunda Ley de Newton:
Newton nunca declaró explícitamente la fórmula en la forma reducida anterior.
La Segunda Ley de Newton afirma la proporcionalidad directa de la aceleración a la fuerza y la proporcionalidad inversa de la aceleración a la masa. Las aceleraciones se pueden definir a través de mediciones cinemáticas. Sin embargo, mientras que la cinemática está bien descrita a través del análisis de marcos de referencia en la física avanzada, aún quedan preguntas profundas sobre cuál es la definición adecuada de masa. La relatividad general ofrece una equivalencia entre el espacio-tiempo y la masa, pero al carecer de una teoría coherente de la gravedad cuántica, no está claro cómo o si esta conexión es relevante en microescalas. Con alguna justificación, la segunda ley de Newton puede tomarse como una definición cuantitativa de masa al escribir la ley como una igualdad; las unidades relativas de fuerza y masa entonces son fijas.
El uso de la Segunda Ley de Newton como una definición de fuerza ha sido menospreciado en algunos de los libros de texto más rigurosos, porque es esencialmente una perogrullada matemática. Físicos, filósofos y matemáticos notables que han buscado una definición más explícita del concepto de fuerza incluyen a Ernst Mach y Walter Noll.
La segunda ley de Newton se puede usar para medir la fuerza de las fuerzas. Por ejemplo, el conocimiento de las masas de planetas junto con las aceleraciones de sus órbitas permite a los científicos calcular las fuerzas gravitacionales en los planetas.
Tercera ley
Cada vez que un cuerpo ejerce una fuerza sobre otro, este ejerce simultáneamente una fuerza igual y opuesta sobre el primero. En forma de vector, si es la fuerza del cuerpo 1 en el cuerpo 2 y la del cuerpo 2 en el cuerpo 1, entonces
Esta ley se refiere a veces como la ley de acción-reacción , la llamada de la acción y la reacción.
La Tercera Ley de Newton es el resultado de aplicar la simetría a situaciones donde las fuerzas se pueden atribuir a la presencia de diferentes objetos. La tercera ley significa que todas las fuerzas son interacciones entre diferentes cuerpos, y por lo tanto que no existe tal cosa como una fuerza unidireccional o una fuerza que actúa sobre un solo cuerpo.
En un sistema compuesto por el objeto 1 y el objeto 2, la fuerza neta en el sistema debido a sus interacciones mutuas es cero:
De manera más general, en un sistema cerrado de partículas, todas las fuerzas internas están equilibradas. Las partículas pueden acelerarse una con respecto a la otra, pero el centro de masa del sistema no se acelerará. Si una fuerza externa actúa sobre el sistema, hará que el centro de masa se acelere en proporción a la magnitud de la fuerza externa dividida por la masa del sistema.
Al combinar las Leyes Segunda y Tercera de Newton, es posible mostrar que se conserva el momento lineal de un sistema. En un sistema de dos partículas, si es el impulso del objeto 1 y el impulso del objeto 2, entonces
Usando argumentos similares, esto se puede generalizar a un sistema con un número arbitrario de partículas. En general, mientras todas las fuerzas se deban a la interacción de objetos con masa, es posible definir un sistema tal que el momento neto nunca se pierda ni se gane.
Teoría especial de la relatividad
En la teoría especial de la relatividad, la masa y la energía son equivalentes (como se puede ver al calcular el trabajo requerido para acelerar un objeto). Cuando la velocidad de un objeto aumenta, también lo hace su energía y, por lo tanto, su equivalente de masa (inercia). Por lo tanto, requiere más fuerza para acelerarlo la misma cantidad que lo hizo a una velocidad inferior. Segunda ley de Newton
sigue siendo válido porque es una definición matemática. Pero para que se conserve el impulso relativista, debe redefinirse como:
dónde está el resto de la masa y la velocidad de la luz.
La expresión relativista que relaciona la fuerza y la aceleración para una partícula con masa de reposo constante distinta de cero moviéndose en la dirección es:
dónde
se llama el factor de Lorentz.
En la historia temprana de la relatividad, las expresiones y se llamaron masa longitudinal y transversal. La fuerza relativista no produce una aceleración constante, sino una aceleración cada vez menor a medida que el objeto se aproxima a la velocidad de la luz. Tenga en cuenta que se aproxima asintóticamente a un valor infinito y no está definido para un objeto con una masa en reposo distinta de cero a medida que se acerca a la velocidad de la luz, y la teoría no produce predicción a esa velocidad.
Si es muy pequeño comparado con , entonces está muy cerca de 1 y
es una aproximación cercana. Incluso para su uso en la relatividad, sin embargo, uno puede restaurar la forma de
mediante el uso de cuatro vectores. Esta relación es correcta en relatividad cuando es la fuerza de cuatro, es la masa invariante, y es la aceleración de cuatro.
Descripciones
Dado que las fuerzas se perciben como empujones o tirones, esto puede proporcionar una comprensión intuitiva para describir las fuerzas. Al igual que con otros conceptos físicos (por ejemplo, la temperatura), la comprensión intuitiva de las fuerzas se cuantifica utilizando definiciones operativas precisas que son consistentes con las observaciones directas y se comparan con una escala de medición estándar. A través de la experimentación, se determina que las mediciones de las fuerzas en el laboratorio son totalmente consistentes con la definición conceptual de la fuerza ofrecida por la mecánica newtoniana.
Las fuerzas actúan en una dirección particular y tienen tamaños que dependen de cuán fuerte es el empuje o el tirón. Debido a estas características, las fuerzas se clasifican como "cantidades vectoriales". Esto significa que las fuerzas siguen un conjunto diferente de reglas matemáticas que las cantidades físicas que no tienen dirección (denotadas cantidades escalares). Por ejemplo, al determinar qué sucede cuando dos fuerzas actúan sobre el mismo objeto, es necesario conocer tanto la magnitud como la dirección de ambas fuerzas para calcular el resultado. Si estas dos piezas de información no se conocen para cada fuerza, la situación es ambigua. Por ejemplo, si sabes que dos personas tiran de la misma cuerda con una magnitud de fuerza conocida pero no sabes qué dirección está tirando ninguna de las dos personas, es imposible determinar cuál será la aceleración de la cuerda. Las dos personas podrían estar tirando una contra la otra como en un tira y afloja o las dos personas podrían estar tirando en la misma dirección. En este sencillo ejemplo unidimensional, sin conocer la dirección de las fuerzas, es imposible decidir si la fuerza neta es el resultado de sumar las dos magnitudes de fuerza o sustraer una de la otra. Asociar fuerzas con vectores evita tales problemas.
Históricamente, las fuerzas fueron primero investigadas cuantitativamente en condiciones de equilibrio estático donde varias fuerzas se anulaban entre sí. Tales experimentos demuestran las propiedades cruciales de que las fuerzas son cantidades de vectores aditivos: tienen magnitud y dirección. Cuando dos fuerzas actúan sobre una partícula puntual, la fuerza resultante, la resultante (también llamada fuerza neta)), puede determinarse siguiendo la regla de paralelogramo de la suma de vectores: la suma de dos vectores representados por lados de un paralelogramo, da un vector resultante equivalente que es igual en magnitud y dirección a la transversal del paralelogramo. La magnitud de la resultante varía de la diferencia de las magnitudes de las dos fuerzas a su suma, dependiendo del ángulo entre sus líneas de acción. Sin embargo, si las fuerzas están actuando sobre un cuerpo extendido, sus líneas de aplicación respectivas también deben especificarse para tener en cuenta sus efectos sobre el movimiento del cuerpo.
Los diagramas de cuerpo libre se pueden utilizar como una forma conveniente de realizar un seguimiento de las fuerzas que actúan en un sistema. Idealmente, estos diagramas se dibujan con los ángulos y las magnitudes relativas de los vectores de fuerza conservados de modo que se pueda hacer una adición gráfica de vectores para determinar la fuerza neta.
Además de agregarse, las fuerzas también se pueden resolver en componentes independientes en ángulo recto entre sí. Por lo tanto, una fuerza horizontal que apunta hacia el noreste se puede dividir en dos fuerzas, una apuntando hacia el norte y otra hacia el este. La suma de estas fuerzas componentes usando la suma vectorial produce la fuerza original. La resolución de vectores de fuerza en componentes de un conjunto de vectores de base es a menudo una forma matemáticamente más limpia para describir fuerzas que el uso de magnitudes y direcciones. Esto se debe a que, para componentes ortogonales, los componentes de la suma del vector están determinados de manera única por la adición escalar de los componentes de los vectores individuales. Los componentes ortogonales son independientes entre sí porque las fuerzas que actúan a noventa grados entre sí no tienen ningún efecto sobre la magnitud o dirección del otro. La elección de un conjunto de vectores de base ortogonal a menudo se realiza al considerar qué conjunto de vectores de base hará que las matemáticas sean más convenientes. Es deseable elegir un vector de base que esté en la misma dirección que una de las fuerzas, ya que esa fuerza tendría entonces solo un componente distinto de cero. Los vectores de fuerza ortogonal pueden ser tridimensionales, y el tercer componente está en ángulo recto con los otros dos.
Equilibrio
El equilibrio ocurre cuando la fuerza resultante que actúa sobre una partícula puntual es cero (es decir, la suma vectorial de todas las fuerzas es cero). Cuando se trata de un cuerpo extendido, también es necesario que el par neto sea cero.
Hay dos tipos de equilibrio: equilibrio estático y equilibrio dinámico.
Estático
El equilibrio estático se entendió mucho antes de la invención de la mecánica clásica. Los objetos que están en reposo tienen una fuerza neta cero actuando sobre ellos.
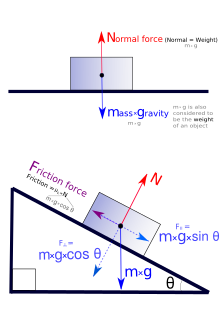
El caso más simple de equilibrio estático ocurre cuando dos fuerzas son iguales en magnitud pero opuestas en dirección. Por ejemplo, un objeto en una superficie nivelada es tirado (atraído) hacia abajo hacia el centro de la Tierra por la fuerza de la gravedad. Al mismo tiempo, la superficie aplica una fuerza que resiste la fuerza hacia abajo con la misma fuerza hacia arriba (llamada fuerza normal). La situación produce una fuerza neta cero y, por lo tanto, no hay aceleración.
Empujar contra un objeto que descansa sobre una superficie de fricción puede dar lugar a una situación en la que el objeto no se mueve porque la fuerza aplicada se opone a la fricción estática, generada entre el objeto y la superficie de la mesa. Para una situación sin movimiento, la fuerza de fricción estática equilibra exactamente la fuerza aplicada y no produce aceleración. La fricción estática aumenta o disminuye en respuesta a la fuerza aplicada hasta un límite superior determinado por las características del contacto entre la superficie y el objeto.
Un equilibrio estático entre dos fuerzas es la forma más habitual de medir fuerzas, utilizando dispositivos simples como básculas y balanzas de resorte. Por ejemplo, un objeto suspendido en una balanza de resorte vertical experimenta la fuerza de la gravedad que actúa sobre el objeto equilibrada por una fuerza aplicada por la "fuerza de reacción del resorte", que es igual al peso del objeto. Usando tales herramientas, se descubrieron algunas leyes cuantitativas de fuerza: que la fuerza de la gravedad es proporcional al volumen para objetos de densidad constante (ampliamente explotada durante milenios para definir pesos estándar); El principio de Arquímedes para la flotabilidad; El análisis de Arquímedes de la palanca; La ley de Boyle para presión de gas; y la ley de Hooke para resortes. Todos fueron formulados y verificados experimentalmente antes de que Isaac Newton expusiera sus Tres leyes del movimiento.
Dinámica
El equilibrio dinámico fue descrito por primera vez por Galileo, quien notó que ciertas suposiciones de la física aristotélica eran contradichas por las observaciones y la lógica. Galileo se dio cuenta de que la adición de velocidad simple exige que el concepto de un "marco de reposo absoluto" no existiera. Galileo concluyó que el movimiento en una velocidad constante era completamente equivalente al descanso. Esto era contrario a la noción de Aristóteles de un "estado natural" de reposo que se acerca naturalmente a los objetos con masa. Los experimentos simples demostraron que la comprensión de Galileo de la equivalencia entre velocidad constante y reposo era correcta. Por ejemplo, si un navegante arroja una bala de cañón desde el nido de cuervos de un barco que se mueve a una velocidad constante, la física aristotélica haría que la bala de cañón caiga directamente hacia abajo mientras el barco se mueve debajo de él. Así, en un universo aristotélico, la bala de cañón que caía aterrizaría detrás del pie del mástil de una nave en movimiento. Sin embargo, cuando este experimento se realiza realmente, la bala de cañón siempre cae al pie del mástil, como si la bala de cañón supiera viajar con la nave a pesar de estar separada de ella. Como no se aplica ninguna fuerza horizontal hacia delante sobre la bala de cañón, la única conclusión que queda es que la bala de cañón continúa moviéndose con la misma velocidad que el bote mientras cae. Por lo tanto, no se requiere fuerza para mantener la bala de cañón en movimiento a la velocidad constante hacia adelante. como si la bala de cañón supiera viajar con la nave a pesar de estar separada de ella. Como no se aplica ninguna fuerza horizontal hacia delante sobre la bala de cañón, la única conclusión que queda es que la bala de cañón continúa moviéndose con la misma velocidad que el bote mientras cae. Por lo tanto, no se requiere fuerza para mantener la bala de cañón en movimiento a la velocidad constante hacia adelante. como si la bala de cañón supiera viajar con la nave a pesar de estar separada de ella. Como no se aplica ninguna fuerza horizontal hacia delante sobre la bala de cañón, la única conclusión que queda es que la bala de cañón continúa moviéndose con la misma velocidad que el bote mientras cae. Por lo tanto, no se requiere fuerza para mantener la bala de cañón en movimiento a la velocidad constante hacia adelante.
Además, cualquier objeto que viaje a una velocidad constante debe estar sujeto a una fuerza neta cero (fuerza resultante). Esta es la definición de equilibrio dinámico: cuando todas las fuerzas sobre un objeto se equilibran pero aún se mueve a una velocidad constante.
Un simple caso de equilibrio dinámico ocurre en un movimiento de velocidad constante a través de una superficie con fricción cinética. En tal situación, se aplica una fuerza en la dirección del movimiento mientras que la fuerza de fricción cinética se opone exactamente a la fuerza aplicada. Esto da como resultado una fuerza neta cero, pero como el objeto comenzó con una velocidad distinta de cero, continúa moviéndose con una velocidad distinta de cero. Aristóteles malinterpretó este movimiento como causado por la fuerza aplicada. Sin embargo, cuando se tiene en cuenta la fricción cinética, está claro que no hay fuerza neta que genere un movimiento de velocidad constante.
Fuerzas en mecánica cuántica
La noción de "fuerza" mantiene su significado en la mecánica cuántica, aunque ahora se trata de operadores en lugar de variables clásicas y aunque la física ahora se describe mediante la ecuación de Schrödinger en lugar de las ecuaciones newtonianas. Esto tiene la consecuencia de que los resultados de una medición ahora a veces se "cuantifican", es decir, aparecen en porciones discretas. Esto es, por supuesto, difícil de imaginar en el contexto de "fuerzas". Sin embargo, el potencial V (x, y, z) o campos, desde la cual las fuerzas generalmente se pueden derivar, son tratados de manera similar a las variables de posición clásica, es decir, .
Esto se vuelve diferente solo en el marco de la teoría cuántica de campos, donde estos campos también se cuantifican.
Sin embargo, ya en la mecánica cuántica hay una "advertencia", es decir, las partículas que actúan una sobre la otra no solo poseen la variable espacial, sino también una variable discreta intrínseca similar al momento angular denominada "spin", y está el principio de Pauli. relacionando el espacio y las variables de giro. Dependiendo del valor del giro, las partículas idénticas se dividen en dos clases diferentes, fermiones y bosones. Si dos fermiones idénticos (por ejemplo, electrones) tienen una función de giro simétrica (por ejemplo, espines paralelos) las variables espaciales deben ser antisimétricas (es decir, se excluyen mutuamente de sus lugares como si hubiera una fuerza repulsiva), y viceversa, es decir, antiparalela gira las variables de posición debe ser simétrico (es decir, la fuerza aparente debe ser atractiva). Por lo tanto, en el caso de dos fermiones hay una correlación estrictamente negativa entre las variables espaciales y de espín, mientras que para dos bosones (p. Ej., Cuantos de ondas electromagnéticas, fotones) la correlación es estrictamente positiva.
Por lo tanto, la noción de "fuerza" ya pierde parte de su significado.
Diagramas de Feynman
En la física de partículas moderna, las fuerzas y la aceleración de las partículas se explican como un subproducto matemático del intercambio de bosones gauge de impulso. Con el desarrollo de la teoría cuántica de campos y la relatividad general, se descubrió que la fuerza es un concepto redundante que surge de la conservación del momento (4-momento en la relatividad y el momento de partículas virtuales en la electrodinámica cuántica). La conservación del impulso puede derivarse directamente de la homogeneidad o simetría del espacio y, por lo tanto, se considera más fundamental que el concepto de una fuerza. Por lo tanto, las fuerzas fundamentales actualmente conocidas se consideran con mayor precisión como "interacciones fundamentales". Cuando la partícula A emite (crea) o absorbe (aniquila) la partícula virtual B, una conservación de impulso da como resultado el retroceso de la partícula A produciendo una impresión de repulsión o atracción entre las partículas AA 'intercambiadas por B. Esta descripción se aplica a todas las fuerzas que surgen de las interacciones fundamentales. Si bien se necesitan descripciones matemáticas sofisticadas para predecir, con todo detalle, el resultado preciso de tales interacciones, existe una forma conceptualmente simple de describir tales interacciones mediante el uso de diagramas de Feynman. En un diagrama de Feynman, cada partícula de materia se representa como una línea recta (ver línea del mundo) que viaja a través del tiempo, que normalmente aumenta hacia arriba o hacia la derecha en el diagrama. Las partículas de materia y antimateria son idénticas, excepto por su dirección de propagación a través del diagrama de Feynman. Las líneas mundiales de partículas se cruzan en los vértices de interacción, y el diagrama de Feynman representa cualquier fuerza que surge de una interacción que ocurre en el vértice con un cambio instantáneo asociado en la dirección de las líneas del mundo de partículas. Los bosones de calibre se emiten lejos del vértice como líneas onduladas y, en el caso del intercambio de partículas virtual, se absorben en un vértice adyacente.
La utilidad de los diagramas de Feynman es que otros tipos de fenómenos físicos que son parte de la imagen general de las interacciones fundamentales pero que están conceptualmente separados de las fuerzas también se pueden describir usando las mismas reglas. Por ejemplo, un diagrama de Feynman puede describir con detalles sucintos cómo un neutrón se descompone en un electrón, protón y neutrino, una interacción mediada por el mismo bosón gauge que es responsable de la fuerza nuclear débil.
Fuerzas fundamentales
Todas las fuerzas en el universo se basan en cuatro interacciones fundamentales. Las fuerzas fuertes y débiles son fuerzas nucleares que actúan solo a distancias muy cortas y son responsables de las interacciones entre las partículas subatómicas, incluidos los nucleones y los núcleos compuestos. La fuerza electromagnética actúa entre cargas eléctricas, y la fuerza gravitatoria actúa entre masas. Todas las otras fuerzas en la naturaleza se derivan de estas cuatro interacciones fundamentales. Por ejemplo, la fricción es una manifestación de la fuerza electromagnética que actúa entre los átomos de dos superficies, y el principio de exclusión de Pauli, que no permite que los átomos se atraviesen entre sí. De manera similar, las fuerzas en resortes, modeladas por la ley de Hooke, son el resultado de fuerzas electromagnéticas y el Principio de Exclusión que actúan en conjunto para devolver un objeto a su posición de equilibrio.
Las teorías fundamentales para las fuerzas desarrolladas a partir de la unificación de ideas dispares. Por ejemplo, Isaac Newton unificó, con su teoría universal de la gravedad, la fuerza responsable de los objetos que caen cerca de la superficie de la Tierra con la fuerza responsable de la caída de los cuerpos celestes alrededor de la Tierra (la Luna) y el Sol (los planetas) . Michael Faraday y James Clerk Maxwell demostraron que las fuerzas eléctricas y magnéticas se unificaron a través de una teoría del electromagnetismo. En el siglo XX, el desarrollo de la mecánica cuántica condujo a la comprensión moderna de que las tres primeras fuerzas fundamentales (todas menos la gravedad) son manifestaciones de la materia (fermiones) que interactúan intercambiando partículas virtuales llamadas bosones de calibre. Este modelo estándar de física de partículas asume una similitud entre las fuerzas y llevó a los científicos a predecir la unificación de las fuerzas débiles y electromagnéticas en la teoría electrodébil, que posteriormente fue confirmada por la observación. La formulación completa del modelo estándar predice un mecanismo de Higgs aún no observado, pero las observaciones como las oscilaciones de neutrinos sugieren que el modelo estándar es incompleto. Una gran teoría unificada que permite la combinación de la interacción electrodébil con la fuerza fuerte se presenta como una posibilidad con teorías candidatas como la supersimetría propuesta para acomodar algunos de los problemas no resueltos en física. Los físicos todavía están intentando desarrollar modelos de unificación autoconsistentes que combinen las cuatro interacciones fundamentales en una teoría del todo.
| Propiedad / Interacción | Gravitación | Débiles | Electromagnético | Fuerte | |
|---|---|---|---|---|---|
| (Electroweak) | Fundamental | Residual | |||
| Actúa en: | Masa - Energía | Sabor | Carga eléctrica | Carga de color | Núcleos atómicos |
| Partículas experimentando: | Todas | Quarks, leptons | Cargado eléctricamente | Quarks, Gluons | Hadrones |
| Partículas mediadoras: | Graviton (aún no observado) | W W Z | γ | Gluons | Mesones |
| Fuerza en la escala de quarks: | 10 | 10 | 1 | 60 | No aplicable a los quarks |
| Fuerza en la escala de protones / neutrones: | 10 | 10 | 1 | No aplicable a los hadrones | 20 |
Gravitacional
Lo que ahora llamamos gravedad no se identificó como una fuerza universal hasta el trabajo de Isaac Newton. Antes de Newton, la tendencia de los objetos a caer hacia la Tierra no se entendía como relacionada con los movimientos de los objetos celestes. Galileo fue instrumental en la descripción de las características de los objetos que caen al determinar que la aceleración de cada objeto en caída libre era constante e independiente de la masa del objeto. Hoy en día, esta aceleración debido a la gravedad hacia la superficie de la Tierra generalmente se designa como y tiene una magnitud de aproximadamente 9.81 metros por segundo al cuadrado (esta medida se toma del nivel del mar y puede variar según la ubicación), y apunta hacia el centro de la Tierra. Esta observación significa que la fuerza de la gravedad en un objeto en la superficie de la Tierra es directamente proporcional a la masa del objeto. Por lo tanto, un objeto que tiene una masa de experimentará una fuerza:
Para un objeto en caída libre, esta fuerza no tiene oposición y la fuerza neta sobre el objeto es su peso. Para los objetos que no están en caída libre, la fuerza de la gravedad se opone por las fuerzas de reacción aplicadas por sus soportes. Por ejemplo, una persona parada en el suelo experimenta una fuerza neta cero, ya que una fuerza normal (una fuerza de reacción) es ejercida por el suelo hacia arriba sobre la persona que contrarresta su peso que se dirige hacia abajo.
La contribución de Newton a la teoría gravitatoria fue unificar los movimientos de los cuerpos celestes, que Aristóteles había asumido que estaban en un estado natural de movimiento constante, con movimiento decreciente observado en la Tierra. Propuso una ley de la gravedad que podría explicar los movimientos celestes que se habían descrito anteriormente utilizando las leyes del movimiento planetario de Kepler.
Newton se dio cuenta de que los efectos de la gravedad podrían observarse de diferentes maneras a distancias mayores. En particular, Newton determinó que la aceleración de la Luna alrededor de la Tierra podría atribuirse a la misma fuerza de gravedad si la aceleración debida a la gravedad disminuyera como una ley del cuadrado inverso. Además, Newton se dio cuenta de que la aceleración de un cuerpo debido a la gravedad es proporcional a la masa del otro cuerpo atrayente. La combinación de estas ideas proporciona una fórmula que relaciona la masa ( ) y el radio ( ) de la Tierra con la aceleración gravitacional:
donde la dirección del vector viene dada por , el vector unidad se dirige hacia afuera desde el centro de la Tierra.
En esta ecuación, se usa una constante dimensional para describir la fuerza relativa de la gravedad. Esta constante se conoce como la constante de gravitación universal de Newton, aunque su valor era desconocido en la vida de Newton. No fue hasta 1798 que Henry Cavendishable hizo la primera medición de usar un equilibrio de torsión; esto fue ampliamente reportado en la prensa como una medida de la masa de la Tierra ya que el conocimiento podría permitirle a uno resolver la masa de la Tierra dada la ecuación anterior. Newton, sin embargo, se dio cuenta de que dado que todos los cuerpos celestes seguían las mismas leyes del movimiento, su ley de la gravedad tenía que ser universal. Expuesto sucintamente, la Ley de Gravitación de Newton establece que la fuerza sobre un objeto esférico de masa debido a la atracción gravitatoria de la masa es
¿Dónde está la distancia entre los centros de masa de los dos objetos y es el vector unitario apuntando en la dirección alejada del centro del primer objeto hacia el centro del segundo objeto?
Esta fórmula fue lo suficientemente poderosa como para ser la base de todas las descripciones subsecuentes del movimiento dentro del sistema solar hasta el siglo XX. Durante ese tiempo, se inventaron métodos sofisticados de análisis de perturbaciones para calcular las desviaciones de las órbitas debido a la influencia de múltiples cuerpos en un planeta, luna, cometa o asteroide. El formalismo era lo suficientemente exacto para permitir a los matemáticos predecir la existencia del planeta Neptuno antes de que se observara.
La órbita de Mercurio, sin embargo, no coincidía con lo predicho por la Ley de Gravitación de Newton. Algunos astrofísicos predijeron la existencia de otro planeta (Vulcano) que explicaría las discrepancias; sin embargo, no se pudo encontrar ese planeta. Cuando Albert Einstein formuló su teoría de la relatividad general (GR), dirigió su atención al problema de la órbita de Mercurio y descubrió que su teoría añadía una corrección, lo que podría explicar la discrepancia. Esta fue la primera vez que se demostró que la Teoría de la Gravedad de Newton era inexacta.
Desde entonces, la relatividad general ha sido reconocida como la teoría que mejor explica la gravedad. En GR, la gravitación no se ve como una fuerza, sino que los objetos que se mueven libremente en campos gravitacionales viajan bajo su propia inercia en líneas rectas a través del espacio-tiempo curvo, definido como la ruta espacio-temporal más corta entre dos eventos espaciotemporales. Desde la perspectiva del objeto, todo movimiento ocurre como si no hubiera gravitación alguna. Solo cuando se observa el movimiento en un sentido global se puede observar la curvatura del espacio-tiempo y la fuerza se deduce del recorrido curvo del objeto. Por lo tanto, el camino de línea recta en el espacio-tiempo se ve como una línea curva en el espacio, y se llama la trayectoria balística del objeto. Por ejemplo, un basketballthrown del suelo se mueve en una parábola, ya que está en un campo gravitacional uniforme. Su trayectoria espacio-temporal es casi una línea recta, ligeramente curvada (con un radio de curvatura del orden de pocos años luz). La derivada en el tiempo del momento cambiante del objeto es lo que llamamos "fuerza gravitacional".
Electromagnético
La fuerza electrostática fue descrita por primera vez en 1784 por Coulomb como una fuerza que existía intrínsecamente entre dos cargas. Las propiedades de la fuerza electrostática eran que variaba como una ley del cuadrado inverso dirigida en la dirección radial, era atractiva y repulsiva (había polaridad intrínseca), era independiente de la masa de los objetos cargados y seguía el principio de superposición. La ley de Coulomb unifica todas estas observaciones en una declaración sucinta.
Los matemáticos y físicos posteriores encontraron que la construcción del campo eléctrico es útil para determinar la fuerza electrostática en una carga eléctrica en cualquier punto del espacio. El campo eléctrico se basaba en usar una "carga de prueba" hipotética en cualquier lugar del espacio y luego usar la Ley de Coulomb para determinar la fuerza electrostática. Por lo tanto, el campo eléctrico en cualquier lugar del espacio se define como
¿Dónde está la magnitud de la carga hipotética de prueba?
Mientras tanto, se descubrió que la fuerza de magnetismo de Lorentz existía entre dos corrientes eléctricas. Tiene el mismo carácter matemático que la Ley de Coulomb, con la salvedad de que las corrientes similares se atraen y, a diferencia de las corrientes, se repelen. De forma similar al campo eléctrico, el campo magnético puede usarse para determinar la fuerza magnética de una corriente eléctrica en cualquier punto del espacio. En este caso, se determinó que la magnitud del campo magnético era
donde es la magnitud de la corriente de prueba hipotética y es la longitud del cable hipotético a través del cual fluye la corriente de prueba. El campo magnético ejerce una fuerza sobre todos los imanes, incluidos, por ejemplo, los que se utilizan en brújulas. El hecho de que el campo magnético de la Tierra esté alineado estrechamente con la orientación del eje de la Tierra causa que los imanes de la brújula se orienten debido a la fuerza magnética que tira de la aguja.
Al combinar la definición de corriente eléctrica como la tasa de cambio de tiempo de la carga eléctrica, una regla de multiplicación de vectores llamada Ley de Lorentz describe la fuerza sobre una carga que se mueve en un campo magnético. La conexión entre la electricidad y el magnetismo permite la descripción de una fuerza electromagnética unificada que actúa sobre una carga. Esta fuerza se puede escribir como una suma de la fuerza electrostática (debido al campo eléctrico) y la fuerza magnética (debido al campo magnético). Totalmente establecido, esta es la ley:
donde está la fuerza electromagnética, es la magnitud de la carga de la partícula, es el campo eléctrico, es la velocidad de la partícula que se cruza con el campo magnético ( ).
El origen de los campos eléctricos y magnéticos no se explicaría por completo hasta 1864 cuando James Clerk Maxwell unificó varias teorías anteriores en un conjunto de 20 ecuaciones escalares, que luego fueron reformuladas en 4 ecuaciones vectoriales por Oliver Heaviside y Josiah Willard Gibbs. Estas "ecuaciones de Maxwell" describen completamente las fuentes de los campos como cargas estacionarias y móviles, y las interacciones de los campos mismos. Esto llevó a Maxwell a descubrir que los campos eléctricos y magnéticos podían "autogenerarse" a través de una onda que viajaba a una velocidad que calculó como la velocidad de la luz. Esta idea unió los campos nacientes de la teoría electromagnética con la óptica y condujo directamente a una descripción completa del espectro electromagnético.
Sin embargo, intentar conciliar la teoría electromagnética con dos observaciones, el efecto fotoeléctrico y la inexistencia de la catástrofe ultravioleta, resultó problemático. A través del trabajo de destacados físicos teóricos, se desarrolló una nueva teoría del electromagnetismo utilizando la mecánica cuántica. Esta modificación final de la teoría electromagnética condujo finalmente a la electrodinámica cuántica (QED), que describe completamente todos los fenómenos electromagnéticos como mediados por partículas de onda conocidas como fotones. En QED, los fotones son la partícula de intercambio fundamental, que describe todas las interacciones relacionadas con el electromagnetismo, incluida la fuerza electromagnética.
Nuclear fuerte
Hay dos "fuerzas nucleares", que hoy en día se describen generalmente como interacciones que tienen lugar en las teorías cuánticas de la física de partículas. La fuerza nuclear fuerte es la fuerza responsable de la integridad estructural de los núcleos atómicos, mientras que la fuerza nuclear débil es responsable de la descomposición de ciertos nucleones en leptones y otros tipos de hadrones.
Actualmente se entiende que la fuerza fuerte representa las interacciones entre quarks y gluones, tal como se detalla en la teoría de la cromodinámica cuántica (QCD). La fuerza fuerte es la fuerza fundamental mediada por gluones, que actúa sobre quarks, antiquarks y los gluones mismos. La interacción fuerte (acertadamente llamada) es la "más fuerte" de las cuatro fuerzas fundamentales.
La fuerza fuerte solo actúa directamente sobre las partículas elementales. Sin embargo, se observa un residuo de la fuerza entre los hadrones (el ejemplo más conocido es la fuerza que actúa entre nucleones en los núcleos atómicos) como la fuerza nuclear. Aquí la fuerza fuerte actúa indirectamente, se transmite como gluones, que forman parte de los mesones pi y rho virtuales, que clásicamente transmiten la fuerza nuclear (consulte este tema para obtener más información). El fracaso de muchas búsquedas de quarks gratuitos ha demostrado que las partículas elementales afectadas no son directamente observables. Este fenómeno se llama confinamiento de color.
Débil nuclear
La fuerza débil se debe al intercambio de los pesados bosones W y Z. Su efecto más familiar es la desintegración beta (de los neutrones en los núcleos atómicos) y la radioactividad asociada. La palabra "débil" se deriva del hecho de que la intensidad del campo es unas 10 veces menor que la de la fuerza fuerte. Aún así, es más fuerte que la gravedad en distancias cortas. También se ha desarrollado una teoría electrodébil consistente, que muestra que las fuerzas electromagnéticas y la fuerza débil son indistinguibles a temperaturas superiores a aproximadamente 10 kelvins. Dichas temperaturas han sido probadas en modernos aceleradores de partículas y muestran las condiciones del universo en los primeros momentos del Big Bang.
Fuerzas no fundamentales
Algunas fuerzas son consecuencias de las fundamentales. En tales situaciones, los modelos idealizados se pueden utilizar para obtener una visión física.
Fuerza normal
La fuerza normal se debe a las fuerzas de interacción repulsivas entre los átomos en contacto cercano. Cuando sus nubes de electrones se superponen, la repulsión de Pauli (debido a la naturaleza fermiónica de los electrones) sigue dando como resultado la fuerza que actúa en una dirección normal a la superficie de la interfaz entre dos objetos. La fuerza normal, por ejemplo, es responsable de la integridad estructural de las mesas y los pisos, además de ser la fuerza que responde cada vez que una fuerza externa empuja un objeto sólido. Un ejemplo de la fuerza normal en acción es la fuerza de impacto sobre un objeto que choca contra una superficie inmóvil.
Fricción
La fricción es una fuerza superficial que se opone al movimiento relativo. La fuerza de fricción está directamente relacionada con la fuerza normal que actúa para mantener separados dos objetos sólidos en el punto de contacto. Hay dos amplias clasificaciones de fuerzas de fricción: fricción estática y fricción cinética.
La fuerza de fricción estática ( ) se opondrá exactamente a las fuerzas aplicadas a un objeto paralelo a un contacto superficial hasta el límite especificado por el coeficiente de fricción estática ( ) multiplicado por la fuerza normal ( ). En otras palabras, la magnitud de la fuerza de fricción estática satisface la desigualdad:
La fuerza de fricción cinética ( ) es independiente tanto de las fuerzas aplicadas como del movimiento del objeto. Por lo tanto, la magnitud de la fuerza es igual a:
¿Dónde está el coeficiente de fricción cinética? Para la mayoría de las interfaces superficiales, el coeficiente de fricción cinética es menor que el coeficiente de fricción estática.
Tensión
Las fuerzas de tensión se pueden modelar utilizando cuerdas ideales sin masa, sin fricción, irrompibles e imposibles de estirar. Se pueden combinar con poleas ideales, que permiten cadenas ideales para cambiar la dirección física. Las cuerdas ideales transmiten fuerzas de tensión instantáneamente en pares acción-reacción, de modo que si dos objetos están conectados por una cuerda ideal, cualquier fuerza dirigida a lo largo del mismo por el primer objeto va acompañada de una fuerza dirigida por el segundo . Al conectar la misma cadena varias veces al mismo objeto mediante el uso de una configuración que utiliza poleas móviles, la fuerza de tensión en una carga se puede multiplicar. Para cada cuerda que actúa sobre una carga, otro factor de la fuerza de tensión en la cuerda actúa sobre la carga. Sin embargo, a pesar de que tales máquinas permiten un aumento en la fuerza, hay un aumento correspondiente en la longitud de la cuerda que debe ser desplazada para mover la carga. Estos efectos en tándem resultan en última instancia en la conservación de la energía mecánica ya que el trabajo realizado en la carga es el mismo sin importar cuán complicada sea la máquina.
Fuerza elástica
Una fuerza elástica actúa para devolver un resorte a su longitud natural. Un resorte ideal se considera sin masa, sin fricción, irrompible e infinitamente estirable. Dichos resortes ejercen fuerzas que se empujan cuando se contraen, o se tiran cuando se extienden, en proporción al desplazamiento del resorte desde su posición de equilibrio. Esta relación lineal fue descrita por Robert Hooke en 1676, para quien se nombra la ley de Hooke. Si es el desplazamiento, la fuerza ejercida por un resorte ideal es igual a:
donde está la constante de resorte (o fuerza constante), que es particular de la primavera. El signo menos explica la tendencia de la fuerza a actuar en oposición a la carga aplicada.
Mecánica de Medios Continuos
Las leyes de Newton y la mecánica newtoniana en general se desarrollaron primero para describir cómo las fuerzas afectan las partículas puntuales idealizadas en lugar de los objetos tridimensionales. Sin embargo, en la vida real, la materia tiene una estructura extendida y las fuerzas que actúan sobre una parte de un objeto pueden afectar a otras partes de un objeto. Para situaciones en las que el enrejado que mantiene unidos los átomos de un objeto puede fluir, contraerse, expandirse o cambiar de forma, las teorías de la mecánica del continuo describen la forma en que las fuerzas afectan el material. Por ejemplo, en fluidos extendidos, las diferencias en la presión hacen que las fuerzas se dirijan a lo largo de los gradientes de presión de la siguiente manera:
donde está el volumen del objeto en el fluido y es la función escalar que describe la presión en todos los lugares del espacio. Los gradientes de presión y los diferenciales dan como resultado la fuerza de flotación de los fluidos suspendidos en los campos gravitacionales, los vientos en la ciencia atmosférica y la sustentación asociada con la aerodinámica y el vuelo.
Un ejemplo específico de tal fuerza que está asociada con la presión dinámica es la resistencia del fluido: una fuerza corporal que resiste el movimiento de un objeto a través de un fluido debido a la viscosidad. Para el llamado "arrastre de Stokes", la fuerza es aproximadamente proporcional a la velocidad, pero opuesta en la dirección:
dónde:
- es una constante que depende de las propiedades del fluido y las dimensiones del objeto (generalmente el área de la sección transversal), y
- es la velocidad del objeto.
Más formalmente, las fuerzas en la mecánica del continuo se describen completamente por un tensor de tensión con términos que se definen más o menos como
dónde es el área de sección transversal relevante para el volumen para el que se calcula el tensor de tensión. Este formalismo incluye términos de presión asociados con fuerzas que actúan de forma normal al área de la sección transversal (las diagonales matriciales del tensor), así como los ejes de la pared asociados con fuerzas que actúan paralelas al área de la sección transversal (los elementos fuera de la diagonal). El tensor de tensión es responsable de las fuerzas que causan todas las deformaciones (deformaciones), incluidas también las tensiones y compresiones.
Fuerzas ficticias
Hay fuerzas que dependen del marco, lo que significa que aparecen debido a la adopción de marcos de referencia no newtonianos (es decir, no inerciales). Tales fuerzas incluyen la fuerza centrífuga y la fuerza de Coriolis. Estas fuerzas se consideran ficticias porque no existen en marcos de referencia que no se están acelerando. Debido a que estas fuerzas no son genuinas, también se las conoce como "pseudo fuerzas".
En relatividad general, la gravedad se convierte en una fuerza ficticia que surge en situaciones donde el espacio-tiempo se desvía de una geometría plana. Como una extensión, la teoría de cuerdas y la teoría de Kaluza-Klein atribuyen el electromagnetismo y las otras fuerzas fundamentales, respectivamente, a la curvatura de las dimensiones escaladas de forma diferente, lo que en última instancia implicaría que todas las fuerzas son ficticias.
Rotaciones y torque
Las fuerzas que hacen que los objetos extendidos giren se asocian con torques. Matemáticamente, el torque de una fuerza se define en relación con un punto de referencia arbitrario como el producto cruzado:
dónde
- es el vector de posición del punto de aplicación de fuerza con relación al punto de referencia.
El torque es el equivalente de rotación de la fuerza de la misma manera que el ángulo es el equivalente de rotación para la posición, la velocidad angular para la velocidad y el momento angular para el impulso. Como consecuencia de la Primera Ley del Movimiento de Newton, existe una inercia rotacional que asegura que todos los cuerpos mantengan su momento angular a menos que actúen sobre él con un par desbalanceado. Del mismo modo, la Segunda ley del movimiento de Newton se puede usar para derivar una ecuación análoga para la aceleración angular instantánea del cuerpo rígido:
dónde
- es el momento de inercia del cuerpo
- es la aceleración angular del cuerpo.
Esto proporciona una definición para el momento de inercia, que es el equivalente de rotación para la masa. En los tratamientos más avanzados de la mecánica, donde se describe la rotación en un intervalo de tiempo, el momento de inercia debe ser sustituido por el tensor que, cuando se analiza adecuadamente, determina completamente las características de las rotaciones, incluida la precesión y la nutación.
De manera equivalente, la forma diferencial de la Segunda Ley de Newton proporciona una definición alternativa de torque:
- ¿Dónde está el momento angular de la partícula?
La Tercera Ley del Movimiento de Newton requiere que todos los objetos que ejerzan momentos de torsión experimenten pares iguales y opuestos, y por lo tanto también implica directamente la conservación del momento angular para sistemas cerrados que experimentan rotaciones y revoluciones a través de la acción de pares internos.
Fuerza centrípeta
Para un objeto que se acelera en un movimiento circular, la fuerza desequilibrada que actúa sobre el objeto es igual a:
donde está la masa del objeto, es la velocidad del objeto y es la distancia al centro de la trayectoria circular y es el vector unitario que apunta en la dirección radial hacia afuera desde el centro. Esto significa que la fuerza centrípeta desequilibrada que siente cualquier objeto siempre se dirige hacia el centro de la trayectoria curva. Tales fuerzas actúan perpendicularmente al vector de velocidad asociado con el movimiento de un objeto, y por lo tanto no cambian la velocidad del objeto (magnitud de la velocidad), sino solo la dirección del vector de velocidad. La fuerza desequilibrada que acelera un objeto se puede resolver en un componente que es perpendicular a la ruta y uno que es tangencial a la ruta. Esto produce tanto la fuerza tangencial, que acelera el objeto al desacelerarlo o acelerarlo, y la fuerza radial (centrípeta), que cambia su dirección.
Integrales cinemáticas
Las fuerzas se pueden usar para definir una cantidad de conceptos físicos mediante la integración con respecto a las variables cinemáticas. Por ejemplo, la integración con respecto al tiempo da la definición de impulso:
que según la Segunda Ley de Newton debe ser equivalente al cambio en momento (produciendo el teorema Impulse momentum).
Del mismo modo, la integración con respecto a la posición da una definición para el trabajo realizado por una fuerza:
que es equivalente a los cambios en la energía cinética (produciendo el teorema de la energía del trabajo).
Potencia P es la tasa de cambio d W / d t del trabajo W , ya que la trayectoria se extiende mediante un cambio de posición en un intervalo de tiempo d t :
con la velocidad
Energía potencial
En lugar de una fuerza, a menudo el concepto matemáticamente relacionado de un campo de energía potencial se puede utilizar por conveniencia. Por ejemplo, la fuerza gravitacional que actúa sobre un objeto se puede ver como la acción del campo gravitatorio que está presente en la ubicación del objeto. Repetición matemática de la definición de energía (a través de la definición de trabajo), un campo escalar potencial se define como aquel campo cuyo gradiente es igual y opuesto a la fuerza producida en cada punto:
Las fuerzas se pueden clasificar como conservadoras o no conservadoras. Las fuerzas conservadoras son equivalentes al gradiente de un potencial mientras que las fuerzas no conservativas no lo son.
Fuerzas conservadoras
Una fuerza conservadora que actúa sobre un sistema cerrado tiene un trabajo mecánico asociado que permite que la energía se convierta solo entre formas cinéticas o potenciales. Esto significa que para un sistema cerrado, la energía mecánica neta se conserva siempre que una fuerza conservadora actúa en el sistema. La fuerza, por lo tanto, está relacionada directamente con la diferencia en energía potencial entre dos ubicaciones diferentes en el espacio, y puede considerarse como un artefacto del campo potencial de la misma manera que se puede considerar la dirección y la cantidad de un flujo de agua. ser un artefacto del mapa de contorno de la elevación de un área.
Las fuerzas conservadoras incluyen la gravedad, la fuerza electromagnética y la fuerza de la primavera. Cada una de estas fuerzas tiene modelos que dependen de una posición a menudo dada como un vector radial que emana de potenciales esféricamente simétricos. Ejemplos de esto siguen:
Por la gravedad
donde esta la constante gravitacional, y es la masa del objeto n .
Para fuerzas electrostáticas:
donde es la permitividad eléctrica del espacio libre, y es la carga eléctrica del objeto n .
Para las fuerzas de primavera:
donde esta la primavera constante
Fuerzas no conservativas
Para ciertos escenarios físicos, es imposible modelar las fuerzas como debidas al gradiente de potenciales. Esto a menudo se debe a consideraciones macro-físicas que producen fuerzas que surgen de un promedio estadístico macroscópico de microestados. Por ejemplo, la fricción es causada por los gradientes de numerosos potenciales electrostáticos entre los átomos, pero se manifiesta como un modelo de fuerza que es independiente de cualquier vector de posición de macroescala. Las fuerzas no conservativas distintas de la fricción incluyen otras fuerzas de contacto, tensión, compresión y arrastre. Sin embargo, para cualquier descripción suficientemente detallada, todas estas fuerzas son el resultado de las conservadoras ya que cada una de estas fuerzas macroscópicas son los resultados netos de los gradientes de potenciales microscópicos.
La conexión entre las fuerzas no conservativas macroscópicas y las fuerzas conservadoras microscópicas se describe mediante un tratamiento detallado con mecánica estadística. En los sistemas cerrados macroscópicos, las fuerzas no conservativas actúan para cambiar las energías internas del sistema, y a menudo se asocian con la transferencia de calor. De acuerdo con la Segunda ley de la termodinámica, las fuerzas no conservativas necesariamente resultan en transformaciones de energía dentro de sistemas cerrados desde condiciones ordenadas a más aleatorias a medida que aumenta la entropía.
Unidades de medida
La unidad de fuerza SI es el newton (símbolo N), que es la fuerza requerida para acelerar una masa de un kilogramo a una velocidad de un metro por segundo cuadrado, o kg • m • s . La unidad CGS correspondiente es la dina, la fuerza requerida para acelerar una masa de un gramo por un centímetro por segundo al cuadrado, o g • cm • s . Un Newton es por lo tanto igual a 100,000 dinas.
La unidad de fuerza inglesa gravitacional de pie-libra-segundo por segundo es la fuerza-libra (lbf), definida como la fuerza ejercida por la gravedad sobre una masa-libra en el campo gravitacional estándar de 9.80665 m • s . La libra-fuerza proporciona una unidad de masa alternativa: una babosa es la masa que se acelerará en un pie por segundo al cuadrado cuando actúe sobre una libra de fuerza.
Una unidad de fuerza alternativa en un sistema diferente de pie-libra-segundo, el sistema fps absoluto, es la poundal, definida como la fuerza requerida para acelerar una masa de una libra a razón de un pie por segundo al cuadrado. Las unidades de slug y poundal están diseñadas para evitar una constante de proporcionalidad en la Segunda Ley de Newton.
La fuerza de la libra tiene una contraparte métrica, menos utilizada que el newton: la fuerza del kilogramo (kgf) (a veces kilopond), es la fuerza ejercida por la gravedad estándar sobre un kilogramo de masa. La fuerza del kilogramo conduce a una unidad de masa alternativa, pero raramente utilizada: la babosa métrica (a veces mug o hyl) es esa masa que acelera a 1 m • s cuando se somete a una fuerza de 1 kgf. La fuerza del kilogramo no es parte del sistema SI moderno, y generalmente está en desuso; sin embargo, todavía se considera uso para algunos propósitos como la expresión del peso de la aeronave, el empuje del jet, la tensión de los radios de la bicicleta, la configuración de la llave dinamométrica y el par de salida del motor. Otras unidades de fuerza arcanas incluyen el sthène, que es equivalente a 1000 N, y el kip, que es equivalente a 1000 lbf.
| newton (unidad SI) | dina | kilogramo de fuerza, kilopond | libra fuerza | poundal | |
|---|---|---|---|---|---|
| 1 N | ≡ 1 kg⋅m / s | = 10 dyn | ≈ 0.10197 kp | ≈ 0.22481 lbf | ≈ 7.2330 pdl |
| 1 dyn | = 10 N | ≡ 1 g⋅cm / s | ≈ 1.0197 × 10 kp | ≈ 2.2481 × 10 lbf | ≈ 7.2330 × 10 pdl |
| 1 kp | = 9.80665 N | = 980665 dyn | ≡ g n ⋅ (1 kg) | ≈ 2.2046 lbf | ≈ 70.932 pdl |
| 1 lbf | ≈ 4.448222 N | ≈ 444822 dyn | ≈ 0.45359 kp | ≡ g n ⋅ (1 libra) | ≈ 32.174 pdl |
| 1 pdl | ≈ 0.138255 N | ≈ 13825 din | ≈ 0.014098 kp | ≈ 0.031081 lbf | ≡ 1 lb⋅ft / s |
| El valor de g n como se usa en la definición oficial de la fuerza del kilogramo se usa aquí para todas las unidades gravitacionales. | |||||