Velocidad de la luz
Definición
 La luz solar toma alrededor de 8 minutos y 17 segundos para recorrer la distancia promedio desde la superficie del Sol hasta la Tierra. | |
| Valores exactos | |
|---|---|
| metros por segundo | 299 792 458 |
| Longitud de Planck por tiempo de Planck (es decir, unidades de Planck) | 1 |
| Valores aproximados (a tres dígitos significativos) | |
| kilometros por hora | 1 080 000 000 |
| millas por segundo | 186 000 |
| millas por hora | 671 000 000 |
| unidades astronómicas por día | 173 |
| Parsecs por año | 0.307 |
| Tiempos aproximados de recorrido de la señal luminosa | |
| Distancia | Hora |
| un pie | 1.0 ns |
| un metro | 3.3 ns |
| de la órbita geoestacionaria a la Tierra | 119 ms |
| la longitud del ecuador de la Tierra | 134 ms |
| de la luna a la tierra | 1.3 s |
| del Sol a la Tierra (1 UA) | 8.3 min |
| un año luz | 1.0 año |
| un parsec | 3.26 años |
| de la estrella más cercana a Sun ( 1.3 pc ) | 4.2 años |
| desde la galaxia más cercana (la Gran Galaxia enana Canis) a la Tierra | 25 000 años |
| a través de la Vía Láctea | 100 000 años |
| de la Galaxia de Andrómeda a la Tierra | 2,5 millones de años |
| desde la Tierra hasta el borde del universo observable | 46.5 mil millones años |
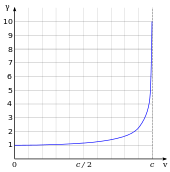
La velocidad a la cual la luz se propaga a través de materiales transparentes, como vidrio o aire, es menor que c ; de manera similar, la velocidad de las ondas electromagnéticas en cables de alambre es más lenta que c . La relación entre cy la velocidad v a la cual la luz viaja en un material se llama índice de refracción n del material ( n = c / v ). Por ejemplo, para la luz visible, el índice de refracción del vidrio es típicamente de alrededor de 1.5, lo que significa que la luz en el vidrio viaja a c / 1.5 ≈ 200,000 km / s (124,000 mi / s); el índice de refracción del aire para la luz visible es de aproximadamente 1.0003, por lo que la velocidad de la luz en el aire es de aproximadamente 299.700 km / s (186,220 mi / s), que es aproximadamente 90 km / s (56 mi / s) más lenta que c .
Para muchos propósitos prácticos, la luz y otras ondas electromagnéticas aparecerán para propagarse instantáneamente, pero para distancias largas y mediciones muy sensibles, su velocidad finita tiene efectos notables. Al comunicarse con sondas espaciales lejanas, un mensaje puede llevar de minutos a horas para que llegue un mensaje de la Tierra a la nave espacial o viceversa. La luz que se ve desde las estrellas los dejó hace muchos años, permitiendo el estudio de la historia del universo al observar objetos distantes. La velocidad finita de la luz también limita la velocidad teórica máxima de las computadoras, ya que la información debe enviarse dentro de la computadora de un chip a otro. La velocidad de la luz se puede usar con el tiempo de las mediciones de vuelo para medir grandes distancias con alta precisión.
Ole Rømer demostró por primera vez en 1676 que la luz viaja a una velocidad finita (en lugar de instantáneamente) mediante el estudio del movimiento aparente de la luna Io de Júpiter. En 1865, James Clerk Maxwell propuso que la luz era una onda electromagnética, y por lo tanto viajó a la velocidad c que aparece en su teoría del electromagnetismo. En 1905, Albert Einstein postuló que la velocidad de la luz c con respecto a cualquier marco inercial es una constante y es independiente del movimiento de la fuente de luz. Exploró las consecuencias de ese postulado al derivar la teoría de la relatividad y al hacerlo mostró que el parámetro c tenía relevancia fuera del contexto de la luz y el electromagnetismo.
Después de siglos de mediciones cada vez más precisas, en 1975 se sabía que la velocidad de la luz era de 299 792 458 m / s ( 983 571 056 pies / s; 186 282.397 mi / s) con una incertidumbre de medición de 4 partes por mil millones. En 1983, el medidor se redefinió en el Sistema Internacional de Unidades (SI) como la distancia recorrida por la luz en el vacío en 1/299 792 458 de segundo.
Valor numérico, notación y unidades
La velocidad de la luz en el vacío generalmente se denota con una c minúscula , para "constante" o las celeritas latinas (que significa "rapidez, celeridad"). En 1856, Wilhelm Eduard Weber y Rudolf Kohlrauschhad utilizan c para una constante diferente más tarde se muestra a la igualdad de √ 2 veces la velocidad de la luz en el vacío. Históricamente, el símbolo V se usó como un símbolo alternativo para la velocidad de la luz, introducido por James Clerk Maxwell en 1865. En 1894, Paul Drude redefinió c con su significado moderno. Einstein usó V en sus documentos originales en alemán sobre relatividad especial en 1905, pero en 1907 cambió a c, que para entonces se había convertido en el símbolo estándar de la velocidad de la luz.
Algunas veces c se usa para la velocidad de las ondas en cualquier medio material, y c 0 para la velocidad de la luz en el vacío. Esta notación subscrita, que está respaldada en la literatura SI oficial, tiene la misma forma que otras constantes relacionadas: a saber, μ 0 para la permeabilidad al vacío o constante magnética, ε 0 para la permitividad del vacío o constante eléctrica, y Z 0 para la impedancia de espacio libre. Este artículo usa c exclusivamente para la velocidad de la luz en el vacío.
Desde 1983, el medidor se ha definido en el Sistema Internacional de Unidades (SI) a medida que la luz de distancia viaja en vacío en / 299 792 458 de segundo. Esta definición corrige la velocidad de la luz en el vacío a exactamente 299,792,458 m / s . Como una constante física dimensional, el valor numérico de c es diferente para diferentes sistemas de unidades. En las ramas de la física en las que c aparece a menudo, como en la relatividad, es común usar sistemas de unidades de medida naturales o el sistema de unidades geometrizadas donde c = 1 . Al usar estas unidades, c no aparece explícitamente porque la multiplicación o división por 1 no afecta el resultado.
Papel fundamental en física
La velocidad a la cual las ondas de luz se propagan en el vacío es independiente tanto del movimiento de la fuente de la onda como del marco de referencia inercial del observador. Esta invariancia de la velocidad de la luz fue postulada por Einstein en 1905, después de haber sido motivada por la teoría del electromagnetismo de Maxwell y la falta de evidencia para el éter luminífero; desde entonces ha sido confirmado constantemente por muchos experimentos. Solo es posible verificar experimentalmente que la velocidad de la luz bidireccional (por ejemplo, de una fuente a un espejo y viceversa) es independiente del cuadro, ya que es imposible medir la velocidad de la luz en una dirección (por ejemplo , de una fuente a un detector distante) sin alguna convención sobre cómo los relojes en la fuente y en el detector deberían sincronizarse. Sin embargo, al adoptar la sincronización de Einstein para los relojes, la velocidad de la luz en una dirección se vuelve igual a la velocidad de la luz bidireccional por definición. La teoría especial de la relatividad explora las consecuencias de esta invariancia de c con la suposición de que las leyes de la física son las mismas en todos los marcos de referencia inerciales. Una consecuencia es que c es la velocidad a la que todas las partículas y ondas sin masa, incluida la luz, deben viajar en el vacío.
La relatividad especial tiene muchas implicaciones contra intuitivas y verificadas experimentalmente. Estos incluyen la equivalencia de masa y energía ( E = mc ) , la contracción de longitud (los objetos en movimiento se acortan) y la dilatación del tiempo (los relojes en movimiento se ejecutan más lentamente). El factor γ por el cual las longitudes se contraen y los tiempos se dilatan se conoce como el factor de Lorentz y está dado por γ = (1 - v / c ) , donde v es la velocidad del objeto. La diferencia de γ de 1 es insignificante para velocidades mucho más lentas que c, como la mayoría de las velocidades diarias, en cuyo caso la relatividad especial se aproxima mucho a la relatividad galileana, pero aumenta a velocidades relativistas y diverge al infinito cuando v se aproxima a c . Por ejemplo, un factor de dilatación de tiempo de γ = 2 ocurre a una velocidad relativa de 86.6% de la velocidad de la luz ( v = .866 c ). De manera similar, un factor de dilatación de tiempo de γ = 10 ocurre en v = 99.5% c .
Los resultados de la relatividad especial se pueden resumir tratando el espacio y el tiempo como una estructura unificada conocida como espaciotiempo ( c relacionando las unidades de espacio y tiempo) y requiriendo que las teorías físicas satisfagan una simetría especial llamada invariancia de Lorentz, cuya formulación matemática contiene parámetro c. La invariancia de Lorenz es una suposición casi universal para las teorías físicas modernas, como la electrodinámica cuántica, la cromodinámica cuántica, el modelo estándar de la física de partículas y la relatividad general. Como tal, el parámetro c es omnipresente en la física moderna, apareciendo en muchos contextos que no están relacionados con la luz. Por ejemplo, la relatividad general predice que c es también la velocidad de la gravedad y de las ondas gravitacionales. En marcos de referencia no inerciales (espaciotiempo curvado gravitacionalmente o marcos de referencia acelerados), la velocidad local de la luz es constante e igual a c , pero la velocidad de la luz a lo largo de una trayectoria de longitud finita puede diferir de c , dependiendo de la distancia y los tiempos están definidos.
En general se supone que las constantes fundamentales como c tienen el mismo valor a lo largo del espacio-tiempo, lo que significa que no dependen de la ubicación y no varían con el tiempo. Sin embargo, se ha sugerido en varias teorías que la velocidad de la luz puede haber cambiado con el tiempo. No se han encontrado pruebas concluyentes de tales cambios, pero siguen siendo objeto de investigaciones en curso.
También se asume generalmente que la velocidad de la luz es isotrópica, lo que significa que tiene el mismo valor independientemente de la dirección en la que se mide. Las observaciones de las emisiones de los niveles de energía nuclear en función de la orientación de los núcleos emisores en un campo magnético (véase el experimento Hughes-Drever) y de los resonadores ópticos giratorios (ver experimentos con resonadores) han puesto límites estrictos a la posible anisotropía.
Límite superior de velocidades
De acuerdo con la relatividad especial, la energía de un objeto con masa en reposo m y velocidad v viene dada por γmc , donde γ es el factor de Lorentz definido anteriormente. Cuando v es cero, γ es igual a uno, lo que da lugar a la famosa fórmula E = mc para la equivalencia masa-energía. El factor γ se acerca al infinito a medida que v se acerca a c, y se necesitaría una cantidad infinita de energía para acelerar un objeto con masa a la velocidad de la luz. La velocidad de la luz es el límite superior para las velocidades de los objetos con masa de reposo positiva, y los fotones individuales no pueden viajar más rápido que la velocidad de la luz. Esto se establece experimentalmente en muchas pruebas de energía relativista e impulso.
De manera más general, normalmente es imposible que la información o la energía viajen más rápido que c . Un argumento para esto se deriva de la implicación contraintuitiva de la relatividad especial conocida como la relatividad de la simultaneidad. Si la distancia espacial entre dos eventos A y B es mayor que el intervalo de tiempo entre ellos multiplicado por c, entonces hay marcos de referencia en los que A precede a B, otros en los que B precede a A, y otros en los que son simultáneos. Como resultado, si algo viajaba más rápido que c en relación con un marco de referencia inercial, estaría viajando hacia atrás en el tiempo en relación con otro marco, y la causalidad sería violada. En ese marco de referencia, se puede observar un "efecto" antes de su "causa". Tal violación de la causalidad nunca se ha registrado, y conduciría a paradojas como el antitelephone taquiónico.
Observaciones y experimentos más rápidos que la luz
Hay situaciones en las que puede parecer que la materia, la energía o la información viajan a velocidades mayores que c , pero no es así. Por ejemplo, como se discute en la propagación de la luz en una sección media a continuación, muchas velocidades de onda pueden exceder c . Por ejemplo, la velocidad de fase de los rayos X a través de la mayoría de los vidrios puede exceder rutinariamente c , pero la velocidad de fase no determina la velocidad a la que las ondas transmiten información.
Si un rayo láser es barrido rápidamente a través de un objeto distante, la mancha de luz puede moverse más rápido que c , aunque el movimiento inicial del punto se retrasa debido al tiempo que tarda la luz en llegar al objeto distante a la velocidad c . Sin embargo, las únicas entidades físicas que se mueven son el láser y su luz emitida, que viaja a la velocidad c desde el láser hasta las diversas posiciones del punto. De forma similar, una sombra proyectada sobre un objeto distante puede moverse más rápido que c , después de un retraso en el tiempo. En ninguno de los casos, cualquier materia, energía o información viaja más rápido que la luz.
La velocidad de cambio en la distancia entre dos objetos en un marco de referencia con respecto a los cuales ambos se mueven (su velocidad de cierre) puede tener un valor en exceso de c . Sin embargo, esto no representa la velocidad de ningún objeto individual medido en un solo cuadro inercial.
Ciertos efectos cuánticos parecen transmitirse instantáneamente y, por lo tanto, más rápido que c, como en la paradoja EPR. Un ejemplo involucra los estados cuánticos de dos partículas que pueden enredarse. Hasta que se observe cualquiera de las partículas, existen en una superposición de dos estados cuánticos. Si las partículas se separan y se observa el estado cuántico de una partícula, el estado cuántico de la otra partícula se determina instantáneamente (es decir, más rápido de lo que la luz podría viajar de una partícula a la otra). Sin embargo, es imposible controlar qué estado cuántico tomará la primera partícula cuando se observe, por lo que la información no se puede transmitir de esta manera.
Otro efecto cuántico que predice la aparición de velocidades más rápidas que la luz se llama efecto Hartman: bajo ciertas condiciones, el tiempo necesario para que una partícula virtual haga un túnel a través de una barrera es constante, independientemente del grosor de la barrera. Esto podría provocar que una partícula virtual cruce un gran espacio más rápido que la luz. Sin embargo, no se puede enviar información utilizando este efecto.
El llamado movimiento superluminal se ve en ciertos objetos astronómicos, como los chorros relativistas de radio galaxias y cuásares. Sin embargo, estos chorros no se mueven a velocidades superiores a la velocidad de la luz: el movimiento superluminal aparente es un efecto de proyección causado por objetos que se mueven cerca de la velocidad de la luz y se aproximan a la Tierra en un ángulo pequeño a la línea de visión: desde la luz que se emitió cuando el chorro estaba más lejos tardó más en llegar a la Tierra, el tiempo entre dos observaciones sucesivas corresponde a un tiempo más largo entre los instantes en los que se emitieron los rayos de luz.
En los modelos del universo en expansión, las galaxias más lejanas se separan, cuanto más rápido se separan. Este retroceso no se debe al movimiento a través del espacio, sino a la expansión del espacio mismo. Por ejemplo, las galaxias lejanas a la Tierra parecen alejarse de la Tierra con una velocidad proporcional a sus distancias. Más allá de un límite llamado esfera Hubble, la velocidad a la que su distancia de la Tierra aumenta es mayor que la velocidad de la luz.
Propagación de luz
En la física clásica, la luz se describe como un tipo de onda electromagnética. El comportamiento clásico del campo electromagnético se describe mediante las ecuaciones de Maxwell, que predicen que la velocidad c con la que las ondas electromagnéticas (como la luz) se propagan a través del vacío se relaciona con la capacitancia distribuida y la inductancia del vacío, conocido también como el constante ε 0 y la constante magnética μ 0 , según la ecuación
En la física cuántica moderna, el campo electromagnético se describe mediante la teoría de la electrodinámica cuántica (QED). En esta teoría, la luz se describe mediante las excitaciones fundamentales (o cuantos) del campo electromagnético, llamadas fotones. En QED, los fotones son partículas sin masa y, de acuerdo con la relatividad especial, viajan a la velocidad de la luz en el vacío.
Se han considerado las extensiones de QED en las que el fotón tiene una masa. En tal teoría, su velocidad dependería de su frecuencia, y la velocidad invariante c de la relatividad especial sería entonces el límite superior de la velocidad de la luz en el vacío. No se ha observado variación de la velocidad de la luz con la frecuencia en pruebas rigurosas, poniendo límites rigurosos sobre la masa del fotón. El límite obtenido depende del modelo utilizado: si el fotón masivo se describe mediante la teoría Proca, el límite superior experimental para su masa es de aproximadamente 10 gramos; si la masa de fotones es generada por un mecanismo de Higgs, el límite superior experimental es menos agudo, m ≤ 10 eV / c (aproximadamente 2 × 10 g).
Otra razón para que la velocidad de la luz varíe con su frecuencia sería la falla de la relatividad especial para aplicarse a escalas arbitrariamente pequeñas, como lo predicen algunas teorías propuestas de la gravedad cuántica. En 2009, la observación del espectro del estallido de rayos gamma GRB 090510 no encontró ninguna diferencia en las velocidades de los fotones de diferentes energías, confirmando que la invarianza de Lorentz se verifica al menos hasta la escala de la longitud de Planck ( l P = √ ħ G / c ≈ 1.6163 × 10 m ) dividido por 1.2.
En un medio
En un medio, la luz por lo general no se propaga a una velocidad igual a c ; Además, diferentes tipos de onda de luz viajarán a diferentes velocidades. La velocidad a la que se propagan las crestas y valles individuales de una onda plana (una onda que llena todo el espacio, con una sola frecuencia) se denomina velocidad de fase v p . Una señal física real con una extensión finita (un pulso de luz) viaja a una velocidad diferente. La mayor parte del pulso viaja a la velocidad del grupo v g , y su parte más temprana viaja a la velocidad frontal v f .
La velocidad de fase es importante para determinar cómo una onda de luz viaja a través de un material o de un material a otro. A menudo se representa en términos de un índice de refracción . El índice de refracción de un material se define como la relación de c a la velocidad de fase v p en el material: los índices de refracción más grandes indican velocidades más bajas. El índice de refracción de un material puede depender de la frecuencia, intensidad, polarización o dirección de propagación de la luz; en muchos casos, sin embargo, puede tratarse como una constante dependiente del material. El índice de refracción del aire es de aproximadamente 1.0003. Los medios más densos, como el agua, el vidrio y el diamante, tienen índices de refracción de alrededor de 1.3, 1.5 y 2.4, respectivamente, para la luz visible. En materiales exóticos como condensados de Bose-Einstein cerca del cero absoluto, la velocidad efectiva de la luz puede ser de unos pocos metros por segundo. Sin embargo, esto representa retrasar la absorción y re-radiación entre los átomos, al igual que todos más lento-que- c velocidades en sustancias materiales. Como un ejemplo extremo de "ralentización" de la luz en la materia, dos equipos independientes de físicos afirmaron llevar la luz a un "punto muerto" pasando a través de un condensado de Bose-Einstein del elemento rubidio, un equipo de la Universidad de Harvard y el Instituto Rowland para Science en Cambridge, Massachusetts, y el otro en el Harvard-Smithsonian Center for Astrophysics, también en Cambridge. Sin embargo, la descripción popular de que la luz se "detiene" en estos experimentos se refiere solo a que la luz se almacena en los estados excitados de los átomos, y luego se remite en un momento arbitrariamente posterior, como estimulado por un segundo pulso de láser. Durante el tiempo que se había "detenido", había dejado de ser ligero. Este tipo de comportamiento generalmente es microscópicamente cierto de todos los medios transparentes que "ralentizan"
En materiales transparentes, el índice de refracción generalmente es mayor que 1, lo que significa que la velocidad de fase es menor que c . En otros materiales, es posible que el índice de refracción sea más pequeño que 1 para algunas frecuencias; en algunos materiales exóticos incluso es posible que el índice de refracción se vuelva negativo. El requisito de que no se viole la causalidad implica que las partes real e imaginaria de la constante dieléctrica de cualquier material, que corresponde respectivamente al índice de refracción y al coeficiente de atenuación, están vinculadas por las relaciones Kramers-Kronig. En términos prácticos, esto significa que en un material con índice de refracción menor a 1, la absorción de la onda es tan rápida que no se puede enviar ninguna señal más rápido que c .
Un pulso con diferentes velocidades de grupo y fase (que ocurre si la velocidad de fase no es la misma para todas las frecuencias del pulso) se difumina a lo largo del tiempo, un proceso conocido como dispersión. Ciertos materiales tienen una velocidad de grupo excepcionalmente baja (o incluso nula) para ondas de luz, un fenómeno llamado luz lenta, que se ha confirmado en varios experimentos. Lo contrario, las velocidades de grupo que exceden c , también se han demostrado en el experimento. Incluso debería ser posible que la velocidad del grupo se vuelva infinita o negativa, con impulsos que viajan instantáneamente o hacia atrás en el tiempo.
Ninguna de estas opciones, sin embargo, permite que la información se transmita más rápido que c . Es imposible transmitir información con un pulso de luz más rápido que la velocidad de la parte más temprana del pulso (la velocidad frontal). Se puede demostrar que esto es (bajo ciertas suposiciones) siempre igual a c .
Es posible que una partícula viaje a través de un medio más rápido que la velocidad de fase de la luz en ese medio (pero aún más lento que c ). Cuando una partícula cargada hace eso en un material dieléctrico, se emite el equivalente electromagnético de una onda de choque, conocida como radiación Cherenkov.
Efectos prácticos de la finitud
La velocidad de la luz es relevante para las comunicaciones: el tiempo de retardo unidireccional y de ida y vuelta es mayor que cero. Esto se aplica desde escalas pequeñas hasta astronómicas. Por otro lado, algunas técnicas dependen de la velocidad finita de la luz, por ejemplo, en mediciones de distancia.
Escalas pequeñas
En los supercomputadores, la velocidad de la luz impone un límite a la rapidez con que se pueden enviar los datos entre los procesadores. Si un procesador opera a 1 gigahertz, una señal solo puede viajar un máximo de aproximadamente 30 centímetros (1 pie) en un solo ciclo. Por lo tanto, los procesadores deben colocarse uno cerca del otro para minimizar las latencias de comunicación; esto puede causar dificultad con el enfriamiento. Si las frecuencias de reloj continúan aumentando, la velocidad de la luz eventualmente se convertirá en un factor limitante para el diseño interno de chips individuales.
Grandes distancias en la Tierra
Dado que la circunferencia ecuatorial de la Tierra es de aproximadamente 40 075 km y que c es de aproximadamente 300 000 km / s , el tiempo teórico más corto para que una información viaje la mitad del globo a lo largo de la superficie es de aproximadamente 67 milisegundos. Cuando la luz viaja por todo el mundo en una fibra óptica, el tiempo de tránsito real es más largo, en parte porque la velocidad de la luz es más lenta en aproximadamente un 35% en una fibra óptica, dependiendo de su índice de refracción n . Además, las líneas rectas rara vez se producen en situaciones de comunicaciones globales, y se crean retrasos cuando la señal pasa a través de un interruptor electrónico o regenerador de señal.
Vuelos espaciales y astronomía
Del mismo modo, las comunicaciones entre la Tierra y la nave espacial no son instantáneas. Hay un breve retraso desde la fuente hasta el receptor, que se hace más notorio a medida que aumentan las distancias. Este retraso fue significativo para las comunicaciones entre el control terrestre y el Apollo 8 cuando se convirtió en la primera nave espacial tripulada en orbitar la Luna: para cada pregunta, la estación de control terrestre tenía que esperar al menos tres segundos para que llegara la respuesta. El retraso de comunicaciones entre la Tierra y Marte puede variar entre cinco y veinte minutos, dependiendo de las posiciones relativas de los dos planetas. Como consecuencia de esto, si un robot en la superficie de Marte encontrara un problema, sus controladores humanos no lo sabrían hasta al menos cinco minutos después, y posiblemente hasta veinte minutos después;
La NASA debe esperar varias horas para obtener información de una sonda que orbita alrededor de Júpiter, y si necesita corregir un error de navegación, la solución no llegará a la nave espacial por el mismo tiempo, creando un riesgo de que la corrección no llegue a tiempo.
Recibir luz y otras señales de fuentes astronómicas distantes puede incluso tomar mucho más tiempo. Por ejemplo, la luz ha tardado 13 mil millones (13 × 10) años en viajar a la Tierra desde las galaxias lejanas que se ven en las imágenes del campo ultra profundo de Hubble. Esas fotografías, tomadas hoy, capturan imágenes de las galaxias tal como aparecieron hace 13 mil millones de años, cuando el universo tenía menos de mil millones de años. El hecho de que los objetos más distantes parezcan más jóvenes, debido a la velocidad finita de la luz, permite a los astrónomos inferir la evolución de las estrellas, de las galaxias y del universo mismo.
Las distancias astronómicas a veces se expresan en años luz, especialmente en publicaciones y medios de divulgación científica. Un año luz es la distancia que la luz viaja en un año, alrededor de 9461 mil millones de kilómetros, 5879 mil millones de millas o 0,3066 parsecs. En cifras redondas, un año luz es de casi 10 billones de kilómetros o casi 6 billones de millas. Proxima Centauri, la estrella más cercana a la Tierra después del Sol, está a unos 4,2 años luz de distancia.
Medida de distancia
Los sistemas de radar miden la distancia a un objetivo en el tiempo que tarda un impulso de onda de radio para regresar a la antena del radar después de ser reflejado por el objetivo: la distancia al objetivo es la mitad del tiempo de ida y vuelta multiplicado por la velocidad de la luz . Un receptor del Sistema de Posicionamiento Global (GPS) mide su distancia a los satélites GPS en función del tiempo que le lleva a una señal de radio llegar desde cada satélite, y desde estas distancias calcula la posición del receptor. Debido a que la luz viaja alrededor de 300 000 kilómetros ( 186 000 mi) en un segundo, estas medidas de fracciones pequeñas de segundo deben ser muy precisas. El Lunar Laser Ranging Experiment, la astronomía de radar y la Deep Space Network determinan las distancias a la Luna, los planetas y las naves espaciales, respectivamente, midiendo los tiempos de tránsito de ida y vuelta.
Comercio de alta frecuencia
La velocidad de la luz se ha vuelto importante en el comercio de alta frecuencia, donde los operadores buscan obtener ventajas mínimas entregando sus intercambios fracciones de segundo por delante de otros operadores. Por ejemplo, los comerciantes han cambiado a las comunicaciones de microondas entre centros comerciales, debido a la ventaja de que las microondas que viajan casi a la velocidad de la luz en el aire, tienen señales de fibra óptica que viajan 30-40% más lento a la velocidad de la luz a través del vidrio .
Medición
Hay diferentes formas de determinar el valor de c . Una forma es medir la velocidad real a la que se propagan las ondas de luz, lo que se puede hacer en varias configuraciones astronómicas y terrestres. Sin embargo, también es posible determinar c a partir de otras leyes físicas donde aparece, por ejemplo, determinando los valores de las constantes electromagnéticas ε
0 y μ
0 y usando su relación con c . Históricamente, los resultados más precisos se han obtenido al determinar por separado la frecuencia y la longitud de onda de un haz de luz, con su producto igualando c .
0 y μ
0 y usando su relación con c . Históricamente, los resultados más precisos se han obtenido al determinar por separado la frecuencia y la longitud de onda de un haz de luz, con su producto igualando c .
En 1983, el medidor se definió como "la longitud del camino recorrido por la luz en el vacío durante un intervalo de tiempo de / 299 792 458 de un segundo", fijando el valor de la velocidad de la luz en 299 792 458 m / s por definición, como se describe abajo. En consecuencia, las mediciones precisas de la velocidad de la luz producen una realización precisa del medidor en lugar de un valor preciso de c .
Mediciones astronómicas
El espacio exterior es una configuración conveniente para medir la velocidad de la luz debido a su gran escala y vacío casi perfecto. Típicamente, uno mide el tiempo necesario para que la luz atraviese alguna distancia de referencia en el sistema solar, como el radio de la órbita de la Tierra. Históricamente, tales mediciones podrían hacerse con bastante precisión, en comparación con la precisión con que se conoce la longitud de la distancia de referencia en las unidades basadas en la Tierra. Es costumbre expresar los resultados en unidades astronómicas (AU) por día.
Ole Christensen Rømer utilizó una medida astronómica para hacer la primera estimación cuantitativa de la velocidad de la luz. Cuando se miden desde la Tierra, los períodos de las lunas que orbitan alrededor de un planeta distante son más cortos cuando la Tierra se acerca al planeta que cuando la Tierra está retrocediendo. La distancia recorrida por la luz del planeta (o su luna) a la Tierra es más corta cuando la Tierra está en el punto de su órbita que está más cerca de su planeta que cuando la Tierra está en el punto más alejado de su órbita, la diferencia de distancia siendo el diámetro de la órbita de la Tierra alrededor del Sol. El cambio observado en el período orbital de la luna es causado por la diferencia en el tiempo que tarda la luz en atravesar la distancia más corta o más larga. Rømer observó este efecto para Júpiter
Otro método es usar la aberración de la luz, descubierta y explicada por James Bradley en el siglo XVIII. Este efecto resulta de la adición del vector de la velocidad de la luz que llega desde una fuente distante (como una estrella) y la velocidad de su observador (ver diagrama a la derecha). Por lo tanto, un observador en movimiento ve que la luz proviene de una dirección ligeramente diferente y, en consecuencia, ve la fuente en una posición desplazada de su posición original. Dado que la dirección de la velocidad de la Tierra cambia continuamente a medida que la Tierra orbita alrededor del Sol, este efecto hace que la posición aparente de las estrellas se mueva. A partir de la diferencia angular en la posición de las estrellas (máximo 20.5 segundos de arco), es posible expresar la velocidad de la luz en términos de la velocidad de la Tierra alrededor del Sol, que con la duración conocida de un año se puede convertir al tiempo necesario para viajar desde el Sol a la Tierra. En 1729, Bradley usó este método para derivar que la luz viajaba 10,210 veces más rápido que la Tierra en su órbita (la cifra moderna es 10,066 veces más rápida) o, de manera equivalente, que tomaría una luz de 8 minutos y 12 segundos para viajar del Sol al Tierra.
Unidad astronómica
Una unidad astronómica (AU) es aproximadamente la distancia promedio entre la Tierra y el Sol. Se redefinió en 2012 como exactamente 149 597 870 700 m. Anteriormente, la AU no se basaba en el Sistema Internacional de Unidades, sino en términos de la fuerza gravitacional ejercida por el Sol en el marco de la mecánica clásica. La definición actual usa el valor recomendado en metros para la definición previa de la unidad astronómica, que se determinó por medición. Esta redefinición es análoga a la del medidor, y del mismo modo tiene el efecto de fijar la velocidad de la luz a un valor exacto en unidades astronómicas por segundo (a través de la velocidad exacta de la luz en metros por segundo).
Anteriormente, el inverso de c expresado en segundos por unidad astronómica se medía comparando el tiempo de las señales de radio para llegar a diferentes naves espaciales en el Sistema Solar, con su posición calculada a partir de los efectos gravitacionales del Sol y varios planetas. Combinando muchas de tales medidas, podría obtenerse un mejor valor de ajuste para el tiempo de luz por distancia de unidad. Por ejemplo, en 2009, la mejor estimación, según lo aprobado por la Unión Astronómica Internacional (UAI), fue:
- tiempo de luz para la distancia de la unidad: t au = 499.004 783 836 (10) s
- c = 0.002 003 988 804 10 (4) AU / s = 173.144 632 674 (3) AU / día.
La incertidumbre relativa en estas mediciones es de 0.02 partes por billón ( 2 × 10 ), lo que equivale a la incertidumbre en mediciones de longitud basadas en la Tierra por interferometría. Dado que el metro se define como la longitud recorrida por la luz en un intervalo de tiempo determinado, la medición del tiempo de luz en términos de la definición previa de la unidad astronómica también puede interpretarse como la medición de la longitud de una AU (antigua definición) en metros.
Tiempo de vuelo
Un método para medir la velocidad de la luz es medir el tiempo necesario para que la luz viaje a un espejo a una distancia y distancia conocidas. Este es el principio de trabajo detrás del aparato Fizeau-Foucault desarrollado por Hippolyte Fizeau y Léon Foucault.
La configuración utilizada por Fizeau consiste en un haz de luz dirigido a un espejo a 8 kilómetros (5 millas) de distancia. En el camino desde la fuente hasta el espejo, el rayo pasa a través de una rueda dentada giratoria. A cierta velocidad de rotación, el rayo pasa a través de un espacio en el camino de salida y otro en el camino de regreso, pero a velocidades ligeramente más altas o más bajas, el rayo golpea un diente y no pasa por la rueda. Al saber la distancia entre la rueda y el espejo, la cantidad de dientes en la rueda y la velocidad de rotación, se puede calcular la velocidad de la luz.
El método de Foucault reemplaza la rueda dentada por un espejo giratorio. Debido a que el espejo sigue girando mientras la luz viaja hacia el espejo distante y hacia atrás, la luz se refleja desde el espejo giratorio en un ángulo diferente en el camino de salida que en el camino de regreso. A partir de esta diferencia de ángulo, se puede calcular la velocidad de rotación conocida y la distancia al espejo distante de la velocidad de la luz.
Hoy en día, usando osciloscopios con resoluciones de tiempo de menos de un nanosegundo, la velocidad de la luz puede medirse directamente al cronometrar el retraso de un pulso de luz de un láser o un LED reflejado desde un espejo. Este método es menos preciso (con errores del orden del 1%) que otras técnicas modernas, pero a veces se utiliza como un experimento de laboratorio en las clases de física de la universidad.
Constantes electromagnéticas
Una opción para derivar c que no depende directamente de una medición de la propagación de ondas electromagnéticas es usar la relación entre c y la permitividad de vacío ε 0 y la permeabilidad de vacío μ 0 establecida por la teoría de Maxwell: c = 1 / ( ε 0 μ 0 ). La permitividad del vacío puede determinarse midiendo la capacitancia y las dimensiones de un condensador, mientras que el valor de la permeabilidad al vacío se fija exactamente a 4π × 10 H⋅m a través de la definición del amperio. Rosa y Dorsey utilizaron este método en 1907 para encontrar un valor de 299 710± 22 km / s .
Resonancia de la cavidad
Otra forma de medir la velocidad de la luz es medir de forma independiente la frecuencia fy la longitud de onda λ de una onda electromagnética en el vacío. El valor de c se puede encontrar utilizando la relación c = fλ. Una opción es medir la frecuencia de resonancia de un resonador de cavidad. Si las dimensiones de la cavidad de resonancia también se conocen, pueden usarse para determinar la longitud de onda de la onda. En 1946, Louis Essen y AC Gordon-Smith establecieron la frecuencia para una variedad de modos normales de microondas de una cavidad de microondas de dimensiones precisamente conocidas. Las dimensiones se establecieron con una precisión de aproximadamente ± 0,8 μm utilizando calibres calibrados por interferometría. Como la longitud de onda de los modos se conocía a partir de la geometría de la cavidad y de la teoría electromagnética, el conocimiento de las frecuencias asociadas permitió un cálculo de la velocidad de la luz.
El resultado de Essen-Gordon-Smith, 299 792 ± 9 km / s , fue sustancialmente más preciso que los encontrados por técnicas ópticas. En 1950, las medidas repetidas de Essen establecieron un resultado de 299 792 .5 ± 3.0 km / s .
Es posible realizar una demostración familiar de esta técnica, utilizando un horno de microondas y alimentos como malvaviscos o margarina: si se retira el plato giratorio para que el alimento no se mueva, se cocinará más rápido en los antinodes (los puntos en los que la amplitud de la onda) es el más grande), donde comenzará a derretirse. La distancia entre dos de tales puntos es la mitad de la longitud de onda de las microondas; midiendo esta distancia y multiplicando la longitud de onda por la frecuencia de microondas (generalmente mostrada en la parte posterior del horno, típicamente 2450 MHz), se puede calcular el valor de c , "a menudo con menos del 5% de error".
Interferometría
La interferometría es otro método para encontrar la longitud de onda de la radiación electromagnética para determinar la velocidad de la luz. Un haz de luz coherente (por ejemplo, desde un láser), con una frecuencia conocida ( f ), se divide para seguir dos caminos y luego recombinarse. Ajustando la longitud de la trayectoria mientras se observa el patrón de interferencia y midiendo cuidadosamente el cambio en la longitud de la trayectoria, se puede determinar la longitud de onda de la luz ( λ). La velocidad de la luz se calcula utilizando la ecuación c = λf .
Antes del advenimiento de la tecnología láser, se usaron fuentes de radio coherentes para mediciones de interferometría de la velocidad de la luz. Sin embargo, la determinación interferométrica de la longitud de onda se vuelve menos precisa con la longitud de onda y los experimentos fueron así limitados en precisión por la longitud de onda larga (~ 0,4 cm (0,16 in)) de las ondas de radio. La precisión puede mejorarse utilizando luz con una longitud de onda más corta, pero luego se vuelve difícil medir directamente la frecuencia de la luz. Una forma de evitar este problema es comenzar con una señal de baja frecuencia cuya frecuencia puede medirse con precisión, y a partir de esta señal sintetizar progresivamente señales de frecuencia más altas cuya frecuencia puede vincularse a la señal original. Un láser puede entonces bloquearse a la frecuencia, y su longitud de onda puede determinarse usando interferometría. Esta técnica se debió a un grupo de la Oficina Nacional de Estándares (NBS) (que más tarde se convirtió en NIST). Lo usaron en 1972 para medir la velocidad de la luz en el vacío con una incertidumbre fraccional de 3.5 × 10 .
Historia
| <1638 | Galileo, linternas cubiertas | poco concluyente |
| <1667 | Accademia del Cimento, linternas cubiertas | poco concluyente |
| 1675 | Rømer y Huygens, lunas de Júpiter | 220 000 |
| 1729 | James Bradley, aberración de la luz | 301 000 |
| 1849 | Hippolyte Fizeau, rueda dentada | 315 000 |
| 1862 | Léon Foucault, espejo giratorio | 298 000 ± 500 |
| 1907 | Constantes Rosa y Dorsey, EM | 299 710 ± 30 |
| 1926 | Albert A. Michelson, espejo giratorio | 299 796 ± 4 |
| 1950 | Essen y Gordon-Smith , resonador de cavidad | 299 792 .5 ± 3.0 |
| 1958 | KD Froome, radio interferometría | 299 792 .50 ± 0.10 |
| 1972 | Evenson et al. , interferometría láser | 299 792 0,4562 ± 0,0011 |
| 1983 | 17º CGPM, definición del medidor | 299 792 .458 (exacto) |
Hasta principios del período moderno, no se sabía si la luz viajaba instantáneamente o a una velocidad finita muy rápida. El primer examen registrado existente de este tema fue en la antigua Grecia. Los antiguos griegos, los eruditos musulmanes y los científicos europeos clásicos debatieron durante mucho tiempo esto hasta que Rømer proporcionó el primer cálculo de la velocidad de la luz. La Teoría de la Relatividad Especial de Einstein concluyó que la velocidad de la luz es constante independientemente del marco de referencia de uno. Desde entonces, los científicos han proporcionado mediciones cada vez más precisas.
Historia temprana
Empédocles (hacia 490-430 aC) fue el primero en proponer una teoría de la luz y afirmó que la luz tiene una velocidad finita. Sostuvo que la luz era algo en movimiento y, por lo tanto, debe tomarse un tiempo para viajar. Aristóteles argumentó, por el contrario, que "la luz se debe a la presencia de algo, pero no es un movimiento". Euclides y Ptolomeo adelantaron la teoría de la visión de emisión de Empédocles, donde la luz se emite desde el ojo, lo que permite la vista. Basándose en esa teoría, Garza de Alejandría argumentó que la velocidad de la luz debe ser infinita porque los objetos distantes, como las estrellas, aparecen inmediatamente al abrir los ojos.
Los primeros filósofos islámicos estuvieron de acuerdo inicialmente con la visión aristotélica de que la luz no tenía velocidad de viaje. En 1021, Alhazen (Ibn al-Haytham) publicó el Libro de la Óptica , en el que presentaba una serie de argumentos que descartaban la teoría de la emisión de la visión en favor de la teoría de la intromisión ahora aceptada, en la que la luz pasa de un objeto al ojo. Esto llevó a Alhazen a proponer que la luz debe tener una velocidad finita, y que la velocidad de la luz es variable, disminuyendo en cuerpos más densos. Argumentó que la luz es una materia sustancial, cuya propagación requiere tiempo, incluso si esto está oculto a nuestros sentidos. También en el siglo XI, Abū Rayhān al-Bīrūnī acordó que la luz tiene una velocidad finita, y observó que la velocidad de la luz es mucho más rápida que la velocidad del sonido.
En el siglo 13, Roger Bacon argumentó que la velocidad de la luz en el aire no era infinita, utilizando argumentos filosóficos respaldados por la escritura de Alhazen y Aristóteles. En la década de 1270, Witelo consideró la posibilidad de que la luz viajara a una velocidad infinita en el vacío, pero disminuyendo la velocidad en los cuerpos más densos.
A principios del siglo XVII, Johannes Kepler creía que la velocidad de la luz era infinita, ya que el espacio vacío no representa ningún obstáculo para ella. René Descartes argumentó que si la velocidad de la luz fuera finita, el Sol, la Tierra y la Luna se desalinearían notablemente durante un eclipse lunar. Como no se había observado tal desalineación, Descartes concluyó que la velocidad de la luz era infinita. Descartes especuló que si se descubría que la velocidad de la luz era finita, todo su sistema de filosofía podría ser demolido. En la derivación de Descartes de la ley de Snell, supuso que a pesar de que la velocidad de la luz era instantánea, cuanto más denso era el medio, más rápida era la velocidad de la luz. Pierre de Fermat derivó la ley de Snell usando la suposición opuesta, mientras más denso era el medio que viajaba la luz más lenta.
Primeros intentos de medición
En 1629, Isaac Beeckman propuso un experimento en el que una persona observa el destello de un cañón que se refleja en un espejo a una milla (1,6 km) de distancia. En 1638, Galileo Galilei propuso un experimento, con un reclamo aparente de haberlo realizado unos años antes, para medir la velocidad de la luz observando el retraso entre el descubrimiento de una linterna y su percepción a cierta distancia. No pudo distinguir si el viaje ligero fue instantáneo o no, pero llegó a la conclusión de que si no fuera así, debe ser extraordinariamente rápido. En 1667, la Accademia del Cimento de Florencia informó que había realizado el experimento de Galileo, con las linternas separadas por aproximadamente una milla, pero no se observó ninguna demora. La demora real en este experimento habría sido de aproximadamente 11 microsegundos.
La primera estimación cuantitativa de la velocidad de la luz fue hecha en 1676 por Rømer (ver la determinación de Rømer de la velocidad de la luz). A partir de la observación de que los períodos de la luna más interna de Júpiter Io parecían más cortos cuando la Tierra se acercaba a Júpiter que cuando retrocedía, llegó a la conclusión de que la luz viaja a una velocidad finita y estimó que tarda 22 minutos en cruzar el diámetro de Júpiter. La órbita de la Tierra Christiaan Huygens combinó esta estimación con una estimación del diámetro de la órbita de la Tierra para obtener una estimación de la velocidad de la luz de 220 000 km / s , un 26% más bajo que el valor real.
En su libro Optick de 1704 , Isaac Newton informó los cálculos de Rømer de la velocidad finita de la luz y dio un valor de "siete u ocho minutos" por el tiempo que tarda la luz en viajar del Sol a la Tierra (el valor moderno es de 8 minutos 19 segundos). Newton preguntó si las sombras del eclipse de Rømer estaban coloreadas; Al escuchar que no estaban, concluyó que los diferentes colores viajaban a la misma velocidad. En 1729, James Bradley descubrió la aberración estelar. A partir de este efecto, determinó que la luz debe viajar 10,210 veces más rápido que la Tierra en su órbita (la cifra moderna es 10,066 veces más rápida) o, de forma equivalente, que tomaría 8 minutos 12 segundos viajar desde el Sol a la Tierra.
Conexiones con electromagnetismo
En el siglo XIX, Hippolyte Fizeau desarrolló un método para determinar la velocidad de la luz en base a las mediciones de tiempo de vuelo en la Tierra e informó un valor de 315 000 km / s . Su método fue mejorado por Léon Foucault que obtuvo un valor de 298 000 km / s en 1862. En el año 1856, Wilhelm Eduard Weber y Rudolf Kohlrausch midieron la relación de las unidades de carga electromagnéticas y electrostáticas, 1 / √ ε 0 μ 0, descargando un frasco de Leyden, y descubrió que su valor numérico era muy similar a la velocidad de la luz medida directamente por Fizeau. Al año siguiente, Gustav Kirchhoff calculó que una señal eléctrica en un cable sin resistencia viaja a lo largo del cable a esta velocidad. A principios de la década de 1860, Maxwell demostró que, de acuerdo con la teoría del electromagnetismo en la que estaba trabajando, las ondas electromagnéticas se propagaban en el espacio vacío a una velocidad igual a la relación Weber / Kohlrausch anterior y llamaba la atención sobre la proximidad numérica de este valor al La velocidad de la luz medida por Fizeau, propuso que la luz es de hecho una onda electromagnética.
"Éter luminífero"
En ese momento se pensó que el espacio vacío se llenaba con un medio de fondo llamado éter luminífero en el que existía el campo electromagnético. Algunos físicos pensaron que este éter actuó como un marco de referencia preferido para la propagación de la luz y, por lo tanto, debería ser posible medir el movimiento de la Tierra con respecto a este medio, midiendo la isotropía de la velocidad de la luz. A partir de la década de 1880 se realizaron varios experimentos para tratar de detectar este movimiento, el más famoso de los cuales es el experimento realizado por Albert A. Michelson y Edward W. Morley en 1887. El movimiento detectado siempre fue menor que el error observacional. Los experimentos modernos indican que la velocidad de la luz bidireccional es isotrópica (la misma en todas las direcciones) dentro de los 6 nanómetros por segundo. Debido a este experimento, Hendrik Lorentz propuso que el movimiento del aparato a través del éter puede provocar que el aparato se contraiga a lo largo de su longitud en la dirección del movimiento, y además asumió que la variable de tiempo para sistemas móviles también debe cambiarse en consecuencia (" hora local "), que condujo a la formulación de la transformación de Lorentz. Con base en la teoría del éter de Lorentz, Henri Poincaré (1900) demostró que esta hora local (para primer orden en v / c) está indicada por relojes que se mueven en el éter, que se sincronizan bajo el supuesto de una velocidad de luz constante. En 1904, especularon que la velocidad de la luz podría ser una velocidad límite en la dinámica, siempre que las suposiciones de la teoría de Lorentz estén todas confirmadas. En 1905, Poincaré trajo a Lorentz '
Relatividad especial
En 1905, Einstein postuló desde el principio que la velocidad de la luz en el vacío, medida por un observador no acelerador, es independiente del movimiento de la fuente o el observador. Utilizando esto y el principio de la relatividad como base, derivó en la teoría especial de la relatividad, en la que la velocidad de la luz en el vacío c aparece como una constante fundamental, que también aparece en contextos no relacionados con la luz. Esto hizo que el concepto del éter estacionario (al que Lorentz y Poincaré todavía se adherían) fuera inútil y revolucionó los conceptos de espacio y tiempo.
Mayor precisión de c y redefinición del medidor y segundo
En la segunda mitad del siglo XX, se progresó mucho en el aumento de la precisión de las mediciones de la velocidad de la luz, primero mediante técnicas de resonancia de cavidad y más tarde mediante técnicas de interferómetro láser. Estos fueron ayudados por definiciones nuevas y más precisas del medidor y el segundo. En 1950, Louis Essen determinó la velocidad como 299 792 .5 ± 1 km / s , utilizando la resonancia de la cavidad. Este valor fue adoptado por la 12ª Asamblea General de la Unión Radio-Científica en 1957. En 1960, el medidor se redefinió en términos de la longitud de onda de una línea espectral particular de kriptón-86, y, en 1967, el segundo se redefinió en términos de la frecuencia de transición hiperfina del estado fundamental del cesio-133.
En 1972, utilizando el método del interferómetro láser y las nuevas definiciones, un grupo de la Oficina Nacional de Estándares de los Estados Unidos en Boulder, Colorado determinó que la velocidad de la luz en el vacío era c = 299 792 456 .2 ± 1,1 m / s . Esto fue 100 veces menos incierto que el valor previamente aceptado. La incertidumbre restante se relacionó principalmente con la definición del medidor. Como experimentos similares encontraron resultados comparables para c , la XV Conferencia General de Pesas y Medidas en 1975 recomendó usar el valor 299 792 458 m / s para la velocidad de la luz.
Definir la velocidad de la luz como una constante explícita
En 1983, la 17ª CGPM descubrió que las longitudes de onda de las mediciones de frecuencia y un valor dado para la velocidad de la luz son más reproducibles que el estándar anterior. Mantuvieron la definición de 1967 de segundo, por lo que la frecuencia hiperfina del cesio determinaría ahora tanto el segundo como el metro. Para hacer esto, redefinieron el medidor como: "El medidor es la longitud del camino recorrido por la luz en el vacío durante un intervalo de tiempo de 1/299 792 458 de segundo". Como resultado de esta definición, el valor de la velocidad de la luz en el vacío es exactamente 299 792 458 m / s y se ha convertido en una constante definida en el sistema de unidades SI. Las técnicas experimentales mejoradas que antes de 1983 habrían medido la velocidad de la luz, ya no afectarían el valor conocido de la velocidad de la luz en unidades SI, sino que permitirían una realización más precisa del medidor al medir con mayor precisión la longitud de onda de Krypton-86 y otras fuentes de luz.
En 2011, la CGPM declaró su intención de redefinir las siete unidades básicas SI usando lo que llama "la formulación de constante explícita", donde cada "unidad se define indirectamente al especificar explícitamente un valor exacto para una constante fundamental bien reconocida", como fue hecho para la velocidad de la luz. Propuso una redacción nueva, pero completamente equivalente, de la definición del medidor: "El medidor, símbolo m, es la unidad de longitud; su magnitud se establece fijando el valor numérico de la velocidad de la luz en el vacío para que sea exactamente igual a 299 792 458 cuando se expresa en la unidad SI ms ". Este es uno de los cambios propuestos que se incorporará en la próxima revisión de la SI también denominada Nueva SI .