Wikiblog Cultulandia [es]

En la física newtoniana, la masa se puede generalizar como la cantidad de materia en un objeto. Sin embargo, a velocidades muy altas, la relatividad especial establece que la energía cinética de su movimiento se convierte en una fuente adicional significativa de masa. Por lo tanto, cualquier cuerpo estacionario que tenga masa tiene una cantidad equivalente de energía, y todas las formas de energía resisten la aceleración por una fuerza y tienen atracción gravitacional. En la física moderna, la materia no es un concepto fundamental porque su definición ha resultado difícil de alcanzar.

Fenómenos

Hay varios fenómenos distintos que se pueden usar para medir la masa. Aunque algunos teóricos han especulado que algunos de estos fenómenos podrían ser independientes entre sí, los experimentos actuales no han encontrado diferencias en los resultados, independientemente de cómo se mida:

La masa inercial mide la resistencia de un objeto a ser acelerado por una fuerza (representada por la relación F = ma ).
La masa gravitacional activa mide la fuerza gravitacional ejercida por un objeto.
La masa gravitacional pasiva mide la fuerza gravitacional ejercida sobre un objeto en un campo gravitacional conocido.

La masa de un objeto determina su aceleración en presencia de una fuerza aplicada. La inercia y la masa inercial describen las mismas propiedades de los cuerpos físicos en el nivel cualitativo y cuantitativo respectivamente, por otras palabras, la masa describe cuantitativamente la inercia. Según la segunda ley de movimiento de Newton, si un cuerpo de masa fija m se somete a una única fuerza F , su aceleración a está dada por F / m . La masa de un cuerpo también determina el grado en que genera o se ve afectado por un campo gravitacional. Si un primer cuerpo de masa m A se coloca a una distancia r (centro de masa al centro de masa) de un segundo cuerpo de masa m B , cada cuerpo está sujeto a una fuerza de atracción F g = Gm A m B / r , donde G = 6.67 × 10 N kg m es la "constante de gravitación universal". Esto se conoce a veces como masa gravitacional. Los experimentos repetidos desde el siglo XVII han demostrado que la masa inercial y gravitacional son idénticas; desde 1915, esta observación se ha implicado a priori en el principio de equivalencia de la relatividad general.

Unidades de masa

El kilogramo es una de las siete unidades base SI y una de las tres que se define ad hoc (es decir, sin referencia a otra unidad base).

La unidad de masa estándar del Sistema Internacional de Unidades (SI) es el kilogramo (kg). El kilogramo es de 1000 gramos (g), definido por primera vez en 1795 como un decímetro cúbico de agua en el punto de fusión del hielo. Luego, en 1889, el kilogramo se redefinió como la masa del prototipo de kilogramo internacional y, como tal, es independiente del medidor o de las propiedades del agua. Sin embargo, la masa del prototipo internacional y sus copias nacionales idénticas se han encontrado a la deriva a lo largo del tiempo. Se espera que la redefinición del kilogramo y varias otras unidades cambie el 20 de mayo de 2019, luego de una votación final de la CGPM en noviembre de 2018. La nueva definición usará solo cantidades invariables de naturaleza: la velocidad de la luz, la frecuencia hiperfina del cesio y la constante de Planck.

Se aceptan otras unidades para su uso en SI:

la tonelada (t) (o "tonelada métrica") es igual a 1000 kg.
el electrónvoltio (eV) es una unidad de energía, pero debido a la equivalencia masa-energía puede convertirse fácilmente en una unidad de masa, y se usa a menudo como uno. En este contexto, la masa tiene unidades de eV / c (donde c es la velocidad de la luz). El electronvolt y sus múltiplos, como el MeV (megaelectronvolt), se utilizan comúnmente en la física de partículas.
la unidad de masa atómica (u) es 1/12 de la masa de un átomo de carbono-12, aproximadamente 1,66 × 10 kg . La unidad de masa atómica es conveniente para expresar las masas de átomos y moléculas.

Fuera del sistema SI, otras unidades de masa incluyen:

el slug (sl) es una unidad de masa Imperial (alrededor de 14,6 kg).
la libra (lb) es una unidad de masa y fuerza, utilizada principalmente en los Estados Unidos (alrededor de 0,45 kg o 4,5 N). En contextos científicos donde se necesita distinguir libra (fuerza) y libra (masa), en su lugar se usan unidades SI.
la masa de Planck ( m P ) es la masa máxima de partículas puntuales (aproximadamente 2,18 × 10 kg ). Se usa en física de partículas.
la masa solar ( M ☉ ) se define como la masa del sol. Se usa principalmente en astronomía para comparar masas grandes como estrellas o galaxias (≈ 1,99 × 10 kg ).
la masa de una partícula muy pequeña puede identificarse por su longitud de onda Compton inversa ( 1 cm ≈ 3,52 × 10 kg ).
la masa de una estrella muy grande o un agujero negro puede identificarse con su radio Schwarzschild ( 1 cm ≈ 6.73 × 10 kg ).

Definiciones de masa

La relación entre las propiedades de la masa y sus constantes físicas asociadas. Se cree que cada objeto masivo exhibe las cinco propiedades. Sin embargo, debido a las constantes extremadamente grandes o extremadamente pequeñas, en general es imposible verificar más de dos o tres propiedades para cualquier objeto.

El radio de Schwarzschild ( $r s$ ) representa la capacidad de la masa para causar curvatura en el espacio y el tiempo.
El parámetro gravitacional estándar ( $μ$ ) representa la capacidad de un cuerpo masivo para ejercer fuerzas gravitatorias newtonianas en otros cuerpos.
La masa inercial ( $m$ ) representa la respuesta newtoniana de la masa a las fuerzas.
La energía de reposo ( $E 0$ ) representa la capacidad de la masa para convertirse en otras formas de energía.
La longitud de onda de Compton ( $λ$ ) representa la respuesta cuántica de la masa a la geometría local.

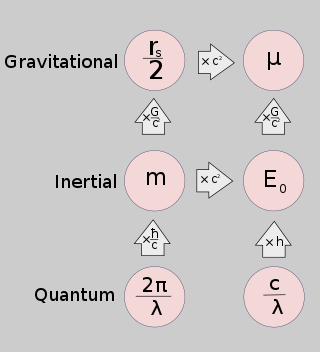
En la ciencia física, uno puede distinguir conceptualmente entre al menos siete aspectos diferentes de la masa , o siete nociones físicas que involucran el concepto de masa . Cada experimento hasta la fecha ha demostrado que estos siete valores son proporcionales, y en algunos casos iguales, y esta proporcionalidad da lugar al concepto abstracto de masa. Hay varias maneras en que se puede medir la masa o definirla operativamente:

La masa inercial es una medida de la resistencia de un objeto a la aceleración cuando se aplica una fuerza. Se determina aplicando una fuerza a un objeto y midiendo la aceleración que resulta de esa fuerza. Un objeto con pequeña masa inercial acelerará más que un objeto con gran masa inercial cuando actúe sobre la misma fuerza. Uno dice que el cuerpo de mayor masa tiene mayor inercia.
La masa gravitacional activa es una medida de la fuerza del flujo gravitacional de un objeto (el flujo gravitatorio es igual a la integral de la superficie del campo gravitacional sobre una superficie circundante). El campo gravitacional se puede medir permitiendo que un pequeño "objeto de prueba" caiga libremente y midiendo su aceleración de caída libre. Por ejemplo, un objeto en caída libre cerca de la Luna está sujeto a un campo gravitacional más pequeño, y por lo tanto acelera más lentamente, que el mismo objeto si estuviera en caída libre cerca de la Tierra. El campo gravitacional cerca de la Luna es más débil porque la Luna tiene una masa gravitacional menos activa.
La masa gravitacional pasiva es una medida de la fuerza de la interacción de un objeto con un campo gravitacional. La masa gravitacional pasiva se determina dividiendo el peso de un objeto por su aceleración de caída libre. Dos objetos dentro del mismo campo gravitatorio experimentarán la misma aceleración; sin embargo, el objeto con una masa gravitacional pasiva más pequeña experimentará una fuerza menor (menos peso) que el objeto con una masa gravitacional pasiva más grande.
La energía también tiene masa según el principio de la equivalencia energía-masa. Esta equivalencia se ejemplifica en una gran cantidad de procesos físicos que incluyen la producción de pares, la fusión nuclear y la flexión gravitacional de la luz. La producción de pares y la fusión nuclear son procesos en los que cantidades de masa medibles se convierten en energía, o viceversa. En la flexión gravitacional de la luz, se muestra que los fotones de energía pura exhiben un comportamiento similar a la masa gravitacional pasiva.
La curvatura del espacio-tiempo es una manifestación relativista de la existencia de la masa. Tal curvatura es extremadamente débil y difícil de medir. Por esta razón, la curvatura no se descubrió hasta que fue predicha por la teoría de la relatividad general de Einstein. Los relojes atómicos extremadamente precisos en la superficie de la Tierra, por ejemplo, se encuentran para medir menos tiempo (correr más lento) en comparación con relojes similares en el espacio. Esta diferencia en el tiempo transcurrido es una forma de curvatura llamada dilatación del tiempo gravitacional. Se han medido otras formas de curvatura usando el satélite Gravity Probe B.
La masa cuántica se manifiesta como una diferencia entre la frecuencia cuántica de un objeto y su número de onda. La masa cuántica de un electrón, la longitud de onda de Compton, puede determinarse a través de diversas formas de espectroscopía y está estrechamente relacionada con la constante de Rydberg, el radio de Bohr y el radio clásico de electrones. La masa cuántica de objetos más grandes se puede medir directamente usando un balance de Watt. En la mecánica cuántica relativista, la masa es una de las etiquetas de representación irreductibles del grupo Poincaré.

Peso vs. masa

En el uso diario, la masa y el "peso" a menudo se usan indistintamente. Por ejemplo, el peso de una persona puede establecerse en 75 kg. En un campo gravitatorio constante, el peso de un objeto es proporcional a su masa, y no es problemático usar la misma unidad para ambos conceptos. Pero debido a pequeñas diferencias en la fuerza del campo gravitacional de la Tierra en diferentes lugares, la distinción se vuelve importante para mediciones con una precisión mejor que un pequeño porcentaje, y para lugares alejados de la superficie de la Tierra, como en el espacio o en otro planetas. Conceptualmente, "masa" (medida en kilogramos) se refiere a una propiedad intrínseca de un objeto, mientras que "peso" (medido en newtons) mide la resistencia de un objeto a desviarse de su curso natural de caída libre, que puede ser influenciado por el campo gravitacional cercano. No importa qué tan fuerte sea el campo gravitatorio, los objetos en caída libre no pesan, aunque todavía tienen masa.

La fuerza conocida como "peso" es proporcional a la masa y la aceleración en todas las situaciones donde la masa se acelera lejos de la caída libre. Por ejemplo, cuando un cuerpo está en reposo en un campo gravitacional (en lugar de en caída libre), debe ser acelerado por una fuerza desde una escala o la superficie de un cuerpo planetario como la Tierra o la Luna. Esta fuerza evita que el objeto caiga en caída libre. El peso es la fuerza opuesta en tales circunstancias, y así está determinado por la aceleración de la caída libre. En la superficie de la Tierra, por ejemplo, un objeto con una masa de 50 kilogramos pesa 491 newtons, lo que significa que se están aplicando 491 newtons para evitar que el objeto caiga en caída libre. Por el contrario, en la superficie de la Luna, el mismo objeto todavía tiene una masa de 50 kilogramos pero pesa solo 81,5 newtons, porque solo 81. Se requieren 5 newtons para evitar que este objeto caiga libremente en la luna. Reformulado en términos matemáticos, en la superficie de la Tierra, el peso W de un objeto está relacionado con su masa m por W = mg , donde g = 9.80665 m / s es la aceleración debida al campo gravitacional de la Tierra (expresada como la aceleración experimentada por un objeto que cae libremente).

Para otras situaciones, como cuando los objetos están sujetos a aceleraciones mecánicas de fuerzas distintas a la resistencia de una superficie planetaria, la fuerza de peso es proporcional a la masa de un objeto multiplicada por la aceleración total lejos de la caída libre, lo que se denomina aceleración. A través de tales mecanismos, los objetos en los ascensores, vehículos, centrífugas y similares pueden experimentar fuerzas de peso muchas veces las causadas por la resistencia a los efectos de la gravedad sobre los objetos, que resultan de las superficies planetarias. En tales casos, la ecuación generalizada para el peso W de un objeto está relacionada con su masa m por la ecuación W = - ma , donde una es la aceleración adecuada del objeto causada por todas las influencias además de la gravedad. (De nuevo, si la gravedad es la única influencia, como ocurre cuando un objeto cae libremente, su peso será cero).

Masa inercial vs. gravitacional

Aunque la masa inercial, la masa gravitacional pasiva y la masa gravitacional activa son conceptualmente distintas, ningún experimento ha demostrado inequívocamente ninguna diferencia entre ellas. En la mecánica clásica, la tercera ley de Newton implica que la masa gravitacional activa y pasiva siempre debe ser idéntica (o al menos proporcional), pero la teoría clásica no ofrece ninguna razón convincente para que la masa gravitacional tenga que igualar la masa inercial. Lo que hace es simplemente un hecho empírico.

Albert Einstein desarrolló su teoría general de la relatividad a partir de la asunción de la intencionalidad de la correspondencia entre la masa inercial y gravitacional pasiva, y que ningún experimento volverá a detectar una diferencia entre ellos, en esencia, el principio de equivalencia.

Esta equivalencia particular, a menudo denominada el "principio de equivalencia de Galileo" o el "principio de equivalencia débil" tiene la consecuencia más importante para los objetos que caen libremente. Supongamos que un objeto con inerciales y gravitacionales masas m y M , respectivamente. Si la única fuerza que actúa sobre el objeto proviene de un campo gravitacional g, la combinación de la segunda ley de Newton y la ley gravitatoria produce la aceleración

a = {\ frac {M} {m}} g.

Esto dice que la relación entre la masa gravitacional y la inercial de cualquier objeto es igual a una constante K si y solo si todos los objetos caen a la misma velocidad en un campo gravitacional dado. Este fenómeno se conoce como la "universalidad de la caída libre". Además, la constante K puede tomarse como 1 al definir nuestras unidades de manera apropiada.

Los primeros experimentos que demostraron la universalidad de la caída libre fueron, según el "folclore" científico, conducidos por Galileo, obtenidos al arrojar objetos desde la Torre Inclinada de Pisa. Esto es muy probable que sea apócrifo: es más probable que haya realizado sus experimentos con bolas rodando por planos inclinados casi sin fricción para frenar el movimiento y aumentar la precisión del tiempo. Se han llevado a cabo experimentos cada vez más precisos, como los realizados por Loránd Eötvös, utilizando el péndulo de equilibrio de torsión, en 1889. Desde 2008, no se ha encontrado ninguna desviación de la universalidad, y por lo tanto de la equivalencia de Galileo, al menos con la precisión 10 Se están llevando a cabo esfuerzos experimentales más precisos.

La universalidad de la caída libre solo se aplica a los sistemas en los cuales la gravedad es la única fuerza actuante. Todas las otras fuerzas, especialmente la fricción y la resistencia del aire, deben estar ausentes o al menos insignificantes. Por ejemplo, si un martillo y una pluma se caen desde la misma altura a través del aire en la Tierra, la pluma tardará mucho más en llegar al suelo; la pluma no está realmente libre- caída porque la fuerza de la resistencia del aire hacia arriba contra la pluma es comparable a la fuerza de la gravedad hacia abajo. Por otro lado, si el experimento se realiza en un vacío, en el que no hay resistencia al aire, el martillo y la pluma deben tocar el suelo exactamente al mismo tiempo (suponiendo la aceleración de ambos objetos entre sí, y del terreno hacia ambos objetos, por su parte, es insignificante). Esto se puede hacer fácilmente en un laboratorio de la escuela secundaria arrojando los objetos en tubos transparentes que tienen el aire eliminado con una bomba de vacío. Es aún más dramático cuando se realiza en un entorno que naturalmente tiene un vacío, como lo hizo David Scott en la superficie de la Luna durante el Apollo 15.

Una versión más fuerte del principio de equivalencia, conocido como el principio de equivalencia de Einstein o el principio de equivalencia fuerte , se encuentra en el corazón de la teoría general de la relatividad. El principio de equivalencia de Einstein establece que dentro de regiones suficientemente pequeñas del espacio-tiempo, es imposible distinguir entre una aceleración uniforme y un campo gravitacional uniforme. Por lo tanto, la teoría postula que la fuerza que actúa sobre un objeto masivo causado por un campo gravitacional es el resultado de la tendencia del objeto a moverse en línea recta (en otras palabras, su inercia) y por lo tanto debe ser una función de su masa inercial y la fuerza del campo gravitacional.

Origen de la misa

En la física teórica, un mecanismo de generación masiva es una teoría que intenta explicar el origen de la masa a partir de las leyes más fundamentales de la física. Hasta la fecha, se han propuesto varios modelos diferentes que abogan por diferentes puntos de vista sobre el origen de la masa. El problema se complica por el hecho de que la noción de masa está fuertemente relacionada con la interacción gravitacional, pero una teoría de esta última aún no se ha reconciliado con el modelo de física de partículas actualmente conocido, conocido como el Modelo Estándar.

Conceptos pre-newtonianos

Peso como una cantidad

Representación de las primeras escalas de equilibrio en el Papiro de Hunefer (fechado en la 19ª dinastía, hacia 1285 aC). La escena muestra a Anubis pesando el corazón de Hunefer.

El concepto de cantidad es muy antiguo y es anterior a la historia registrada. Los humanos, en una época temprana, se dieron cuenta de que el peso de una colección de objetos similares era directamente proporcional al número de objetos en la colección:

W_ {n} \ propto n,

donde W es el peso de la colección de objetos similares y n es el número de objetos en la colección. La proporcionalidad, por definición, implica que dos valores tienen una razón constante:

{\ frac {W_ {n}} {n}} = {\ frac {W_ {m}} {m}}

, o equivalente

{\ frac {W_ {n}} {W_ {m}}} = {\ frac {n} {m}}.

Un uso temprano de esta relación es una balanza, que equilibra la fuerza del peso de un objeto con la fuerza del peso de otro objeto. Los dos lados de una balanza están lo suficientemente cerca para que los objetos experimenten campos gravitacionales similares. Por lo tanto, si tienen masas similares, entonces sus pesos también serán similares. Esto permite que la escala, al comparar pesos, también compare masas.

En consecuencia, los estándares de peso históricos a menudo se definieron en términos de cantidades. Los romanos, por ejemplo, usaron la algarroba (quilate o siliqua) como estándar de medición. Si el peso de un objeto era equivalente a 1728 semillas de algarroba, entonces se decía que el objeto pesaba una libra romana. Si, por otro lado, el peso del objeto era equivalente a 144 semillas de algarroba, entonces se decía que el objeto pesaba una onza romana (uncia). La libra romana y la onza se definieron en términos de colecciones de diferentes tamaños del mismo estándar de masa común, la semilla de algarroba. La relación de una onza romana (144 semillas de algarroba) a una libra romana (1728 semillas de algarroba) fue:

{\ frac {\ mathrm {ounce}} {\ mathrm {pound}}} = {\ frac {W_ {144}} {W_ {1728}}} = {\ frac {144} {1728}} = {\ frac {1} {12}}

Movimiento planetario

En 1600 AD, Johannes Kepler buscó empleo con Tycho Brahe, que tenía algunos de los datos astronómicos más precisos disponibles. Usando las observaciones precisas de Brahe del planeta Marte, Kepler pasó los siguientes cinco años desarrollando su propio método para caracterizar el movimiento planetario. En 1609, Johannes Kepler publicó sus tres leyes del movimiento planetario, explicando cómo los planetas orbitan alrededor del Sol. En el modelo planetario final de Kepler, describió las órbitas planetarias como las siguientes trayectorias elípticas con el Sol en un punto focal de la elipse. Kepler descubrió que el cuadrado del período orbital de cada planeta es directamente proporcional al cubo del semieje mayor de su órbita, o equivalentemente, que la relación de estos dos valores es constante para todos los planetas del Sistema Solar.

El 25 de agosto de 1609, Galileo Galilei mostró su primer telescopio a un grupo de mercaderes venecianos, y a principios de enero de 1610, Galileo observó cuatro objetos oscuros cerca de Júpiter, que confundió con estrellas. Sin embargo, después de unos días de observación, Galileo se dio cuenta de que estas "estrellas" de hecho estaban orbitando a Júpiter. Estos cuatro objetos (más tarde llamados las lunas de Galileo en honor de su descubridor) fueron los primeros cuerpos celestes observados para orbitar algo que no sea la Tierra o el Sol. Galileo continuó observando estas lunas durante los siguientes dieciocho meses, y para mediados de 1611 había obtenido estimaciones notablemente precisas para sus períodos.

Caída libre de Galileo

Galileo Galilei (1636)

La distancia recorrida por una bola que cae libremente es proporcional al cuadrado del tiempo transcurrido

En algún momento antes de 1638, Galileo dirigió su atención al fenómeno de los objetos en caída libre, tratando de caracterizar estos movimientos. Galileo no fue el primero en investigar el campo gravitatorio de la Tierra, ni fue el primero en describir con precisión sus características fundamentales. Sin embargo, la confianza de Galileo en la experimentación científica para establecer principios físicos tendría un profundo efecto en las generaciones futuras de científicos. No está claro si estos fueron solo experimentos hipotéticos utilizados para ilustrar un concepto, o si fueron experimentos reales realizados por Galileo, pero los resultados obtenidos de estos experimentos fueron realistas y convincentes. Una biografía del alumno de Galileo, Vincenzo Viviani, afirmaba que Galileo había arrojado bolas del mismo material, pero diferentes masas, de la Torre Inclinada de Pisa para demostrar que su tiempo de descenso era independiente de su masa. En apoyo de esta conclusión, Galileo había propuesto el siguiente argumento teórico: preguntó si dos cuerpos de diferentes masas y diferentes tasas de caída están atados por una cuerda, ¿el sistema combinado cae más rápido porque ahora es más masivo o el encendedor es más ligero? el cuerpo en su caída más lenta detiene el cuerpo más pesado? La única resolución convincente para esta pregunta es que todos los cuerpos deben caer al mismo ritmo. ¿O el cuerpo más liviano en su caída más lenta detiene el cuerpo más pesado? La única resolución convincente para esta pregunta es que todos los cuerpos deben caer al mismo ritmo. ¿O el cuerpo más liviano en su caída más lenta detiene el cuerpo más pesado? La única resolución convincente para esta pregunta es que todos los cuerpos deben caer al mismo ritmo.

Un experimento posterior fue descrito en Dos nuevas ciencias de Galileo, publicado en 1638. Uno de los personajes de ficción de Galileo, Salviati, describe un experimento con una bola de bronce y una rampa de madera. La rampa de madera tenía "12 codos de largo, medio codo de ancho y tres dedos de ancho" con una ranura recta, lisa y pulida. La ranura estaba forrada con "pergamino, también liso y pulido como sea posible". Y en esta ranura se colocó "una bola de bronce dura, lisa y muy redonda". La rampa estaba inclinada en varios ángulos para ralentizar la aceleración lo suficiente como para poder medir el tiempo transcurrido. Se permitió que la pelota rodara una distancia conocida por la rampa, y se midió el tiempo necesario para que la pelota se moviera a la distancia conocida. El tiempo se midió usando un reloj de agua descrito de la siguiente manera:

"un recipiente grande de agua colocado en una posición elevada, al fondo de este recipiente se soldó una tubería de pequeño diámetro que arrojaba un chorro de agua, que recogimos en un vaso pequeño durante el tiempo de cada descenso, ya sea para el conjunto longitud del canal o por una parte de su longitud, el agua así recolectada se pesó, después de cada descenso, en un equilibrio muy preciso, las diferencias y proporciones de estos pesos nos dieron las diferencias y proporciones de los tiempos, y esto con tal precisión de que, aunque la operación se repitió muchas, muchas veces, no hubo discrepancias apreciables en los resultados ".

Galileo encontró que para un objeto en caída libre, la distancia que el objeto ha caído siempre es proporcional al cuadrado del tiempo transcurrido:

{\ text {Distance}} \ propto {{\ text {Time}} ^ {2}}

Galileo había demostrado que los objetos en caída libre bajo la influencia del campo gravitacional de la Tierra tienen una aceleración constante, y el contemporáneo de Galileo, Johannes Kepler, había demostrado que los planetas siguen caminos elípticos bajo la influencia de la masa gravitacional del Sol. Sin embargo, los movimientos de caída libre de Galileo y los movimientos planetarios de Kepler permanecieron distintos durante la vida de Galileo.

Masa newtoniana

Isaac Newton 1689

Luna de la Tierra		Masa de la Tierra
Semieje mayor	Período orbital sideral	Masa de la Tierra
0.002 569 AU	0.074 802 año sideral	$1.2 \ pi ^ {2} \ cdot 10 ^ {- 5} {\ frac {{\ text {AU}} ^ {3}} {{\ text {y}} ^ {2}}} = 3.986 \ cdot 10 ^ {14} {\ frac {{\ text {m}} ^ {3}} {{\ text {s}} ^ {2}}}$
La gravedad de la Tierra	Radio de la Tierra
9.806 65 m / s	6 375 km

Robert Hooke había publicado su concepto de las fuerzas gravitacionales en 1674, afirmando que todos los cuerpos celestes tienen una atracción o poder gravitatorio hacia sus propios centros, y también atraen a todos los otros cuerpos celestes que se encuentran dentro de la esfera de su actividad. Además, afirmó que la atracción gravitacional aumenta en la medida en que el cuerpo se acerca más a su propio centro. En correspondencia con Isaac Newton de 1679 y 1680, Hooke conjeturó que las fuerzas gravitacionales podrían disminuir según el doble de la distancia entre los dos cuerpos. Hooke instó a Newton, que fue un pionero en el desarrollo del cálculo, a trabajar a través de los detalles matemáticos de las órbitas de Kepler para determinar si la hipótesis de Hooke era correcta. Las propias investigaciones de Newton verificaron que Hooke estaba en lo cierto, pero debido a las diferencias personales entre los dos hombres, Newton optó por no revelar esto a Hooke. Isaac Newton guardó silencio acerca de sus descubrimientos hasta 1684, en ese momento le dijo a un amigo, Edmond Halley, que había resuelto el problema de las órbitas gravitacionales, pero había extraviado la solución en su oficina. Después de ser alentado por Halley, Newton decidió desarrollar sus ideas sobre la gravedad y publicar todos sus hallazgos. En noviembre de 1684, Isaac Newton envió un documento a Edmund Halley, ahora perdido pero presumiblemente titulado Newton decidió desarrollar sus ideas sobre la gravedad y publicar todos sus hallazgos. En noviembre de 1684, Isaac Newton envió un documento a Edmund Halley, ahora perdido pero presumiblemente titulado Newton decidió desarrollar sus ideas sobre la gravedad y publicar todos sus hallazgos. En noviembre de 1684, Isaac Newton envió un documento a Edmund Halley, ahora perdido pero presumiblemente titulado De motu corporum in gyrum (en latín para "Sobre el movimiento de los cuerpos en una órbita"). Halley presentó los hallazgos de Newton a la Royal Society of London, con la promesa de que se realizaría una presentación más completa. Newton más tarde registró sus ideas en un conjunto de tres libros, titulado Philosophiæ Naturalis Principia Mathematica (Latín: Principios Matemáticos de la Filosofía Natural ). El primero fue recibido por la Royal Society el 28 de abril de 1685-6; el segundo el 2 de marzo de 1686-7; y el tercero el 6 de abril de 1686-7. La Royal Society publicó toda la colección de Newton a su costa en mayo de 1686-7.

Isaac Newton había salvado la brecha entre la masa gravitatoria de Kepler y la aceleración gravitatoria de Galileo, lo que resultó en el descubrimiento de la siguiente relación que rige ambos:

\ mathbf {g} = - \ mu {\ frac {\ hat {\ mathbf {R}}} {| \ mathbf {R} | ^ {2}}}

donde g es la aceleración aparente de un cuerpo cuando pasa a través de una región del espacio donde existen campos gravitacionales, μ es la masa gravitacional (parámetro gravitatorio estándar) del cuerpo que causa campos gravitacionales, y R es la coordenada radial (la distancia entre el centros de los dos cuerpos).

Al encontrar la relación exacta entre la masa gravitacional de un cuerpo y su campo gravitacional, Newton proporcionó un segundo método para medir la masa gravitacional. La masa de la Tierra puede determinarse utilizando el método de Kepler (desde la órbita de la Luna de la Tierra), o puede determinarse midiendo la aceleración gravitatoria en la superficie de la Tierra y multiplicándola por el cuadrado del radio de la Tierra. La masa de la Tierra es aproximadamente tres millonésimas de la masa del Sol. Hasta la fecha, no se ha descubierto ningún otro método preciso para medir la masa gravitacional.

Bala de cañón de Newton

Un cañón en la cima de una montaña muy alta dispara una bala de cañón horizontalmente. Si la velocidad es baja, la bala de cañón cae rápidamente a la Tierra (A, B). A velocidades intermedias, girará alrededor de la Tierra a lo largo de una órbita elíptica (C, D). A una velocidad suficientemente alta, dejará la Tierra por completo (E).

La bala de cañón de Newton fue un experimento de pensamiento utilizado para cerrar la brecha entre la aceleración gravitacional de Galileo y las órbitas elípticas de Kepler. Apareció en el libro de 1728 de Newton Un tratado del sistema del mundo. De acuerdo con el concepto de gravitación de Galileo, una piedra caída cae con aceleración constante hacia la Tierra. Sin embargo, Newton explica que cuando una piedra se arroja horizontalmente (es decir, hacia los lados o perpendicular a la gravedad de la Tierra) sigue un camino curvado. "Porque una piedra proyectada es por la presión de su propio peso forzada fuera del camino rectilíneo, que por la proyección solo debería haber seguido, y hecho describir una línea curva en el aire, y a través de ese camino tortuoso finalmente es llevado hasta el suelo. Y cuanto mayor es la velocidad con la que se proyecta, más lejos se encuentra antes de que caiga sobre la Tierra ". Newton además razona que si un objeto se "proyectara en una dirección horizontal desde la cima de una montaña alta" con suficiente velocidad "

Masa gravitacional universal

Una manzana experimenta campos gravitacionales dirigidos hacia cada parte de la Tierra; sin embargo, la suma total de estos muchos campos produce un único campo gravitacional dirigido hacia el centro de la Tierra

En contraste con teorías anteriores (por ejemplo, esferas celestes) que afirmaban que los cielos estaban hechos de material completamente diferente, la teoría de la masa de Newton fue pionera porque introdujo la masa gravitacional universal: cada objeto tiene masa gravitacional y, por lo tanto, cada objeto genera una gravedad campo. Newton asumió además que la fuerza del campo gravitacional de cada objeto disminuiría de acuerdo con el cuadrado de la distancia a ese objeto. Si se formaba una gran colección de pequeños objetos en un cuerpo esférico gigante como la Tierra o el Sol, Newton calculaba que la colección crearía un campo gravitacional proporcional a la masa total del cuerpo, e inversamente proporcional al cuadrado de la distancia al centro del cuerpo

Por ejemplo, de acuerdo con la teoría de la gravitación universal de Newton, cada semilla de algarrobo produce un campo gravitacional. Por lo tanto, si uno recolectara una inmensa cantidad de semillas de algarroba y las formara en una esfera enorme, entonces el campo gravitatorio de la esfera sería proporcional al número de semillas de algarroba en la esfera. Por lo tanto, debería ser teóricamente posible determinar el número exacto de semillas de algarroba que se necesitarían para producir un campo gravitacional similar al de la Tierra o el Sol. De hecho, por conversión de unidades es una simple cuestión de abstracción darse cuenta de que cualquier unidad de masa tradicional puede usarse teóricamente para medir la masa gravitacional.

Dibujo de la sección vertical del instrumento de equilibrio de torsión de Cavendish, incluido el edificio en el que se encuentra. Las bolas grandes se colgaron de un marco para que pudieran girarse en posición junto a las bolas pequeñas con una polea desde el exterior. Figura 1 del papel de Cavendish.

La medición de la masa gravitacional en términos de unidades de masa tradicionales es simple en principio, pero extremadamente difícil en la práctica. De acuerdo con la teoría de Newton, todos los objetos producen campos gravitacionales y teóricamente es posible recolectar una inmensa cantidad de objetos pequeños y formarlos en una enorme esfera gravitatoria. Sin embargo, desde un punto de vista práctico, los campos gravitacionales de objetos pequeños son extremadamente débiles y difíciles de medir. Los libros de Newton sobre la gravitación universal se publicaron en la década de 1680, pero la primera medición exitosa de la masa de la Tierra en términos de unidades de masa tradicionales, el experimento de Cavendish, no ocurrió hasta 1797, más de cien años después. Cavendish descubrió que la densidad de la Tierra era 5.448 ± 0.033 veces mayor que la del agua. A partir de 2009, la Tierra '

Dado dos objetos A y B, de masas M A y M B , separados por un desplazamiento R AB , la ley de gravitación de Newton establece que cada objeto ejerce una fuerza gravitatoria sobre el otro, de magnitud

\ mathbf {F} _ {\ text {AB}} = - GM _ {\ text {A}} M _ {\ text {B}} {\ frac {{\ hat {\ mathbf {R}}} _ {\ text {AB}}} {| \ mathbf {R} _ {\ text {AB}} | ^ {2}}} \

,

donde G es la constante gravitacional universal. La afirmación anterior se puede reformular de la siguiente manera: si g es la magnitud en una ubicación dada en un campo gravitacional, entonces la fuerza gravitacional en un objeto con masa gravitacional M es

F = Mg

.

Esta es la base por la cual las masas se determinan mediante pesaje. En las escalas de resorte simple, por ejemplo, la fuerza F es proporcional al desplazamiento de la springbeneath el plato de pesada, según la ley de Hooke, y las escalas se calibran para tomar g en cuenta, lo que permite la masa M a leerse. Suponiendo que el campo gravitacional es equivalente en ambos lados de la balanza, una balanza mide el peso relativo, dando la masa de gravedad relativa de cada objeto.

Masa inercial

Massmeter, un dispositivo para medir la masa inercial de un astronauta en ingravidez. La masa se calcula a través del período de oscilación para una primavera con el astronauta adjunto (Tsiolkovsky State Museum of the History of Cosmonautics)

La masa inercial es la masa de un objeto medida por su resistencia a la aceleración. Esta definición ha sido defendida por Ernst Mach y desde entonces se ha desarrollado en la noción de operacionalismo por Percy W. Bridgman. La definición de masa simple de la mecánica clásica es ligeramente diferente de la definición en la teoría de la relatividad especial, pero el significado esencial es el mismo.

En la mecánica clásica, según la segunda ley de Newton, decimos que un cuerpo tiene una masa m si, en cualquier instante, obedece a la ecuación del movimiento.

\ mathbf {F} = m \ mathbf {a},

donde F es la fuerza resultante que actúa sobre el cuerpo y a es la aceleración del centro de masa del cuerpo. Por el momento, dejaremos de lado la cuestión de qué significa realmente la "fuerza que actúa sobre el cuerpo".

Esta ecuación ilustra cómo la masa se relaciona con la inercia de un cuerpo. Considere dos objetos con masas diferentes. Si aplicamos una fuerza idéntica a cada uno, el objeto con una masa más grande experimentará una aceleración más pequeña, y el objeto con una masa más pequeña experimentará una mayor aceleración. Podríamos decir que la masa más grande ejerce una mayor "resistencia" a cambiar su estado de movimiento en respuesta a la fuerza.

Sin embargo, esta noción de aplicar fuerzas "idénticas" a diferentes objetos nos devuelve al hecho de que no hemos definido realmente qué es una fuerza. Podemos eludir esta dificultad con la ayuda de la tercera ley de Newton, que establece que si un objeto ejerce una fuerza sobre un segundo objeto, experimentará una fuerza igual y opuesta. Para ser precisos, supongamos que tenemos dos objetos de masas inerciales constantes m 1 y m 2 . Aislamos los dos objetos de todas las otras influencias físicas, de modo que las únicas fuerzas presentes son la fuerza ejercida sobre m 1 por m 2 , que denotamos F 12 , y la fuerza ejercida sobre m 2 por m1 , que denotamos F 21 . La segunda ley de Newton establece que

{\ begin {aligned} \ mathbf {F_ {12}} & = m_ {1} \ mathbf {a} _ {1}, \\\ mathbf {F_ {21}} & = m_ {2} \ mathbf {a } _ {2}, \ end {aligned}}

donde a 1 y a 2 son las aceleraciones de m 1 y m 2 , respectivamente. Supongamos que estas aceleraciones no son cero, por lo que las fuerzas entre los dos objetos no son cero. Esto ocurre, por ejemplo, si los dos objetos están colisionando entre sí. La tercera ley de Newton dice que

\ mathbf {F} _ {12} = - \ mathbf {F} _ {21};

y por lo tanto

m_ {1} = m_ {2} {\ frac {| \ mathbf {a} _ {2} |} {| \ mathbf {a} _ {1} |}} \ !.

Si | a 1 | es distinto de cero, la fracción está bien definida, lo que nos permite medir la masa inercial de m 1 . En este caso, m 2 es nuestro objeto de "referencia", y podemos definir su masa m como (digamos) 1 kilogramo. Entonces podemos medir la masa de cualquier otro objeto en el universo colisionándolo con el objeto de referencia y midiendo las aceleraciones.

Además, la masa relaciona el impulso de un cuerpo p con su velocidad lineal v :

\ mathbf {p} = m \ mathbf {v}

,

y la energía cinética K del cuerpo a su velocidad:

K = {\ dfrac {1} {2}} m | \ mathbf {v} | ^ {2}

.

La principal dificultad con la definición de masa de Mach es que no tiene en cuenta la energía potencial (o energía de enlace) necesaria para acercar dos masas lo suficiente para realizar la medición de la masa. Esto se demuestra más vívidamente al comparar la masa del protón en el núcleo del deuterio, con la masa del protón en el espacio libre (que es mayor en alrededor del 0.239%, esto se debe a la energía de enlace del deuterio). Así, por ejemplo, si se toma el peso de referencia m 2 como la masa del neutrón en el espacio libre, y se calculan las aceleraciones relativas para el protón y el neutrón en el deuterio, entonces la fórmula anterior sobreestima la masa m 1 (en 0.239%) para el protón en deuterio. En el mejor de los casos, la fórmula de Mach solo puede usarse para obtener relaciones de masas, es decir, como m 1 / m 2 = | a 2 | / | un 1 |. Henri Poincaré señaló una dificultad adicional, que es que la medición de la aceleración instantánea es imposible: a diferencia de la medición de tiempo o distancia, no hay forma de medir la aceleración con una sola medición; uno debe hacer mediciones múltiples (de posición, tiempo, etc.) y realizar un cálculo para obtener la aceleración. Poincaré lo denominó como un "defecto insalvable" en la definición de masa de Mach.

Masa atomica

Normalmente, la masa de los objetos se mide en relación con la del kilogramo, que se define como la masa del kilogramo prototipo internacional (IPK), un cilindro de aleación de platino almacenado en una caja fuerte con control ambiental asegurada en una bóveda en la Oficina Internacional de Pesas y Medidas en Francia. Sin embargo, el IPK no es conveniente para medir las masas de átomos y partículas de escala similar, ya que contiene trillones de trillones de átomos, y con toda certeza ha perdido o ganado un poco de masa a pesar de los mejores esfuerzos para evitarlo. Es mucho más fácil comparar con precisión la masa de un átomo con la de otro átomo, así los científicos desarrollaron la unidad de masa atómica (o Dalton). Por definición, 1 u es exactamente una doceava parte de la masa de un átomo de carbono-12, y por extensión un átomo de carbono-12 tiene una masa de exactamente 12 u. Esta definición, sin embargo, podría ser modificada por la redefinición propuesta de las unidades base SI, lo que dejará al Dalton muy cerca de uno,

Masa en relatividad

Relatividad especial

En la relatividad especial, hay dos tipos de masa: masa de reposo (masa invariante) y masa relativista (que aumenta con la velocidad). La masa de reposo es la masa newtoniana medida por un observador que se mueve junto con el objeto. La masa relativista es la cantidad total de energía en un cuerpo o sistema dividido por c . Los dos están relacionados por la siguiente ecuación:

m _ {\ mathrm {relative}} = \ gamma (m _ {\ mathrm {rest}}) \!

¿Dónde está el factor de Lorentz?

\gama

\ gamma = {\ frac {1} {\ sqrt {1-v ^ {2} / c ^ {2}}}}

La masa invariante de sistemas es la misma para los observadores en todos los marcos inerciales, mientras que la masa relativista depende del marco de referencia del observador. Para formular las ecuaciones de la física de modo que los valores de masa no cambien entre los observadores, es conveniente usar la masa en reposo. La masa en reposo de un cuerpo también está relacionada con su energía E y la magnitud de su momento p mediante la ecuación relativista energía-momento:

(m _ {\ mathrm {rest}}) c ^ {2} = {\ sqrt {E _ {\ mathrm {total}} ^ {2} - (| \ mathbf {p} | c) ^ {2}}}. \!

Mientras el sistema se cierre con respecto a la masa y la energía, ambos tipos de masa se conservan en cualquier marco de referencia dado. La conservación de la masa se mantiene incluso cuando algunos tipos de partículas se convierten en otros. Las partículas de materia (como los átomos) pueden convertirse en partículas sin materia (como los fotones de luz), pero esto no afecta la cantidad total de masa o energía. Aunque las cosas como el calor pueden no ser materia, todos los tipos de energía continúan exhibiendo masa. Por lo tanto, la masa y la energía no se cambian entre sí en la relatividad; más bien, ambos son nombres para la misma cosa, y ni la masa ni la energía aparecen sin la otra.

Tanto el reposo como la masa relativista se pueden expresar como una energía aplicando la conocida relación E = mc , produciendo energía en reposo y "energía relativista" (energía total del sistema), respectivamente:

E _ {\ mathrm {rest}} = (m _ {\ mathrm {rest}}) c ^ {2} \!

E _ {\ mathrm {total}} = (m _ {\ mathrm {relative}}) c ^ {2} \!

Los conceptos "relativistas" de masa y energía están relacionados con sus contrapartes de "descanso", pero no tienen el mismo valor que sus contrapartes de descanso en sistemas donde hay un impulso neto. Debido a que la masa relativista es proporcional a la energía, gradualmente ha caído en desuso entre los físicos. Existe desacuerdo sobre si el concepto sigue siendo útil pedagógicamente.

En los sistemas ligados, la energía de enlace a menudo se debe restar de la masa del sistema no unido, porque la energía de enlace comúnmente abandona el sistema en el momento en que está ligado. La masa del sistema cambia en este proceso simplemente porque el sistema no se cerró durante el proceso de enlace, por lo que la energía escapó. Por ejemplo, la energía de enlace de los núcleos atómicos a menudo se pierde en forma de rayos gamma cuando se forman los núcleos, dejando núclidos que tienen menos masa que las partículas libres (nucleones) de los que están compuestos.

La equivalencia masa-energía también se mantiene en los sistemas macroscópicos. Por ejemplo, si uno toma exactamente un kilogramo de hielo y aplica calor, la masa del agua fundida resultante será más de un kilogramo: incluirá la masa de la energía térmica (calor latente) utilizada para derretir el hielo; esto se deduce de la conservación de la energía. Este número es pequeño pero no desdeñable: alrededor de 3,7 nanogramos. Está dada por el calor latente del hielo que se derrite (334 kJ / kg) dividido por la velocidad de la luz al cuadrado ( c = 9 × 10 m / s).

Relatividad general

En relatividad general, el principio de equivalencia es cualquiera de varios conceptos relacionados que tratan con la equivalencia de la masa gravitacional e inercial. En el centro de esta afirmación está la idea de Albert Einstein de que la fuerza gravitatoria experimentada localmente mientras está de pie en un cuerpo masivo (como la Tierra) es la misma que la seudo-fuerza experimentada por un observador en un sistema no inercial (es decir, acelerado) marco de referencia.

Sin embargo, resulta que es imposible encontrar una definición general objetiva para el concepto de masa invariante en la relatividad general. En el núcleo del problema está la no linealidad de las ecuaciones de campo de Einstein, lo que hace imposible escribir la energía del campo gravitatorio como parte del tensor de energía de esfuerzo de una manera que es invariante para todos los observadores. Para un observador dado, esto puede lograrse mediante el pseudotensor de energía-momento-estrés.

Masa en física cuántica

En la mecánica clásica, la masa inerte de una partícula aparece en la ecuación de Euler-Lagrange como un parámetro m :

{\ frac {\ mathrm {d}} {\ mathrm {d} t}} \ \ left (\, {\ frac {\ partial L} {\ partial {\ dot {x}} _ {i}}} \ , \ right) \ = \ m \, {\ ddot {x}} _ {i}

.

Después de la cuantificación, reemplazando el vector de posición x con una función de onda, el parámetro m aparece en el operador de energía cinética:

i \ hbar {\ frac {\ partial} {\ partial t}} \ Psi (\ mathbf {r}, \, t) = \ left (- {\ frac {\ hbar ^ {2}} {2m}} \ nabla ^ {2} + V (\ mathbf {r}) \ right) \ Psi (\ mathbf {r}, \, t)

.

En la ecuación de Dirac ostensiblemente covariante (relativísticamente invariante) y en unidades naturales, esto se convierte en:

(-i \ gamma ^ {\ mu} \ partial _ {\ mu} + m) \ psi = 0 \,

donde el parámetro "en masa" m ahora es simplemente una constante asociada con el cuanto descrito por la función de onda ψ.

En el Modelo Estándar de física de partículas desarrollado en la década de 1960, este término surge del acoplamiento del campo ψ a un campo adicional Φ, el campo de Higgs. En el caso de fermiones, el mecanismo de Higgs resulta en el reemplazo del término m ψ en el lagrangiano con . Esto desplaza el explanandum del valor de la masa de cada partícula elemental al valor de los acoplamientos desconocidos G ψ .

G _ {\ psi} {\ overline {\ psi}} \ phi \ psi

Partículas taquionicas y masa imaginaria (compleja)

Un campo taquiónico, o simplemente tachyon, es un campo cuántico con una masa imaginaria. Aunque los taquiones (partículas que se mueven más rápido que la luz) son un concepto puramente hipotético que generalmente no se cree que existen, los campos con masa imaginaria han llegado a jugar un papel importante en la física moderna y se discuten en libros populares sobre física. En ninguna circunstancia, ninguna excitación se propaga más rápido que la luz en tales teorías: la presencia o ausencia de una masa taquiónica no tiene efecto alguno sobre la velocidad máxima de las señales (no hay violación de la causalidad). Mientras el campo puede tener masa imaginaria, cualquier partícula física no; la "masa imaginaria" muestra que el sistema se vuelve inestable y arroja la inestabilidad al experimentar un tipo de transición de fase llamada condensación de taquiones (estrechamente relacionada con transiciones de fase de segundo orden) que da como resultado la ruptura de la simetría en los modelos actuales de física de partículas.

El término "taquión" fue acuñado por Gerald Feinberg en un artículo de 1967, pero pronto se dio cuenta de que el modelo de Feinberg, de hecho, no permitía velocidades superlumínicas. En cambio, la masa imaginaria crea una inestabilidad en la configuración: - cualquier configuración en la que o más excitaciones de campo son taquiónicas se desintegrarán espontáneamente, y la configuración resultante no contiene taquiones físicos. Este proceso se conoce como condensación de taquiones. Los ejemplos bien conocidos incluyen la condensación del bosón de Higgs en la física de partículas y el ferromagnetismo en la física de la materia condensada.

Aunque la noción de una masa imaginaria taquiónica puede parecer problemática porque no existe una interpretación clásica de una masa imaginaria, la masa no se cuantifica. Más bien, el campo escalar es; incluso para los campos cuánticos taquiónicos, los operadores de campo en los puntos separados de la zona espacial todavía conmutan (o anticomuman), preservando así la causalidad. Por lo tanto, la información aún no se propaga más rápido que la luz, y las soluciones crecen exponencialmente, pero no superluminalmente (no hay violación de la causalidad). La condensación de Tachyon maneja un sistema físico que ha alcanzado un límite local y se puede esperar ingenuamente que produzca taquiones físicos, a un estado estable alternativo donde no existen taquiones físicos. Una vez que el campo taquiónico alcanza el mínimo del potencial,

Este es un caso especial de la regla general, donde las partículas masivas inestables se describen formalmente como teniendo una masa compleja, siendo la parte real su masa en el sentido usual, y la parte imaginaria es la tasa de decaimiento en las unidades naturales. Sin embargo, en la teoría cuántica de campos, una partícula (un "estado de una partícula") se define aproximadamente como un estado que es constante a lo largo del tiempo; es decir, un valor propio del hamiltoniano. Una partícula inestable es un estado que es solo aproximadamente constante a lo largo del tiempo; Si existe el tiempo suficiente para ser medido, puede describirse formalmente como tener una masa compleja, con la parte real de la masa mayor que su parte imaginaria. Si ambas partes son de la misma magnitud, esto se interpreta como una resonancia que aparece en un proceso de dispersión en lugar de una partícula, ya que se considera que no existe el tiempo suficiente para ser medido independientemente del proceso de dispersión. En el caso de un taquión, la parte real de la masa es cero y, por lo tanto, no se le puede atribuir ningún concepto de partícula.

En una teoría invariante de Lorentz, las mismas fórmulas que se aplican a las partículas ordinarias más lentas que la luz (a veces llamadas "bradyons" en las discusiones de los taquiones) también deben aplicarse a los taquiones. En particular, la relación energía-momento:

E ^ {2} = p ^ {2} c ^ {2} + m ^ {2} c ^ {4} \;

(donde p es el momento relativista del bradyon y m es su masa en reposo) todavía debe aplicarse, junto con la fórmula para la energía total de una partícula:

E = {\ frac {mc ^ {2}} {\ sqrt {1 - {\ frac {v ^ {2}} {c ^ {2}}}}}}.

Esta ecuación muestra que la energía total de una partícula (bradyon o tachyon) contiene una contribución de su masa en reposo (la "masa-energía en reposo") y una contribución de su movimiento, la energía cinética. Cuando v es mayor que c , el denominador en la ecuación de la energía es "imaginario", ya que el valor bajo el radical es negativo. Como la energía total debe ser real, el numerador también debe ser imaginario: es decir, la masa en reposo m debe ser imaginaria, ya que un número imaginario puro dividido por otro número imaginario puro es un número real.

Materia exótica y masa negativa

La masa negativa existe en el modelo para describir la energía oscura (energía fantasma) y la radiación en metamaterial de índice negativo de una manera unificada. De esta forma, la masa negativa se asocia con impulso negativo, presión negativa, energía cinética negativa y FTL (más rápido que la luz).

Masa

Definición