Mecánica cuántica
Definición
La mecánica cuántica ( QM , también conocida como física cuántica , teoría cuántica , modelo mecánico ondulatorio o mecánica matricial ), incluida la teoría cuántica de campos, es una teoría fundamental en física que describe la naturaleza en las escalas más pequeñas de los niveles de energía de los átomos y las partículas subatómicas.
La física clásica, la física existente antes de la mecánica cuántica, describe la naturaleza a escala ordinaria (macroscópica). La mayoría de las teorías en física clásica se pueden derivar de la mecánica cuántica como una aproximación válida a gran escala (macroscópica). La mecánica cuántica difiere de la física clásica en que la energía, el momento, el momento angular y otras cantidades de un sistema están restringidos a valores discretos (cuantificación); los objetos tienen características de partículas y ondas (dualidad onda-partícula); y hay límites a la precisión con la que se pueden medir las cantidades (principio de incertidumbre).
La mecánica cuántica surgió gradualmente de las teorías para explicar observaciones que no podían conciliarse con la física clásica, como la solución de Max Planck en 1900 al problema de radiación del cuerpo negro y la correspondencia entre energía y frecuencia en el artículo de Albert Einstein de 1905 que explicaba la fotoeléctrica efecto. La teoría cuántica temprana fue profundamente re-concebida a mediados de la década de 1920 por Erwin Schrödinger, Werner Heisenberg, Max Born y otros. La teoría moderna está formulada en varios formalismos matemáticos especialmente desarrollados. En una de ellas, una función matemática, la función de onda, proporciona información sobre la amplitud de probabilidad de posición, momento y otras propiedades físicas de una partícula.
Las aplicaciones importantes de la teoría cuántica incluyen química cuántica, óptica cuántica, computación cuántica, imanes superconductores, diodos emisores de luz y el láser, el transistor y los semiconductores como el microprocesador, imágenes médicas y de investigación, como la resonancia magnética y el microscopio electrónico. Las explicaciones para muchos fenómenos biológicos y físicos están enraizadas en la naturaleza del enlace químico, más notablemente el ADN de la macro-molécula.
Historia
La investigación científica sobre la naturaleza ondulatoria de la luz comenzó en los siglos XVII y XVIII, cuando científicos como Robert Hooke, Christiaan Huygens y Leonhard Euler propusieron una teoría ondulatoria de la luz basada en observaciones experimentales. En 1803, Thomas Young, un polímata inglés, realizó el famoso experimento de doble rendija que describió más tarde en un artículo titulado Sobre la naturaleza de la luz y los colores . Este experimento jugó un papel importante en la aceptación general de la teoría ondulatoria de la luz.
En 1838, Michael Faraday descubrió los rayos catódicos. Estos estudios fueron seguidos por la declaración de 1859 del problema de la radiación del cuerpo negro por Gustav Kirchhoff, la sugerencia de Ludwig Boltzmann en 1877 de que los estados de energía de un sistema físico pueden ser discretos, y la hipótesis cuántica de 1900 de Max Planck. La hipótesis de Planck de que la energía se irradia y se absorbe en discretos "cuantos" (o paquetes de energía) coincide exactamente con los patrones observados de la radiación del cuerpo negro.
En 1896, Wilhelm Wien determinó empíricamente una ley de distribución de la radiación del cuerpo negro, conocida como la ley de Wien en su honor. Ludwig Boltzmann llegó independientemente a este resultado por consideraciones de las ecuaciones de Maxwell. Sin embargo, era válido solo a altas frecuencias y subestimaba la radiancia a bajas frecuencias. Más tarde, Planck corrigió este modelo utilizando la interpretación estadística de la termodinámica de Boltzmann y propuso lo que ahora se llama la ley de Planck, que condujo al desarrollo de la mecánica cuántica.
Siguiendo la solución de Max Planck en 1900 al problema de la radiación del cuerpo negro (reportado en 1859), Albert Einstein ofreció una teoría cuántica para explicar el efecto fotoeléctrico (1905, reportado en 1887). Alrededor de 1900-1910, la teoría atómica y la teoría corpuscular de la luz llegaron a ser ampliamente aceptadas como hechos científicos; estas últimas teorías se pueden ver como teorías cuánticas de la materia y radiación electromagnética, respectivamente.
Entre los primeros en estudiar los fenómenos cuánticos en la naturaleza estuvieron Arthur Compton, CV Raman y Pieter Zeeman, cada uno de los cuales tiene un efecto cuántico que lleva su nombre. Robert Andrews Millikan estudió el efecto fotoeléctrico experimentalmente, y Albert Einstein desarrolló una teoría para ello. Al mismo tiempo, Ernest Rutherford descubrió experimentalmente el modelo nuclear del átomo, para lo cual Niels Bohr desarrolló su teoría de la estructura atómica, que luego fue confirmada por los experimentos de Henry Moseley. En 1913, Peter Debye amplió la teoría de la estructura atómica de Niels Bohr, introduciendo órbitas elípticas, un concepto también introducido por Arnold Sommerfeld. Esta fase se conoce como antigua teoría cuántica.
De acuerdo con Planck, cada elemento de energía ( E ) es proporcional a su frecuencia ( ν ):
- ,
donde h es la constante de Planck.
Planck insistió cautelosamente en que esto era simplemente un aspecto de los procesos de absorción y emisión de radiación y que no tenía nada que ver con la realidad física de la radiación misma. De hecho, consideró su hipótesis cuántica un truco matemático para obtener la respuesta correcta en lugar de un descubrimiento considerable. Sin embargo, en 1905 Albert Einstein interpretó la hipótesis cuántica de Planck de manera realista y la utilizó para explicar el efecto fotoeléctrico, en el que la luz brillante sobre ciertos materiales puede expulsar electrones del material. Ganó el Premio Nobel de Física de 1921 por este trabajo.
Einstein desarrolló aún más esta idea para mostrar que una onda electromagnética como la luz también podría describirse como una partícula (más tarde llamada fotón), con un quantum discreto de energía que dependía de su frecuencia.
Los fundamentos de la mecánica cuántica se establecieron durante la primera mitad del siglo XX por Max Planck, Niels Bohr, Werner Heisenberg, Louis de Broglie, Arthur Compton, Albert Einstein, Erwin Schrödinger, Max Born, John von Neumann, Paul Dirac y Enrico Fermi. , Wolfgang Pauli, Max von Laue, Freeman Dyson, David Hilbert, Wilhelm Wien, Satyendra Nath Bose, Arnold Sommerfeld y otros. La interpretación de Copenhague de Niels Bohr fue ampliamente aceptada.
A mediados de la década de 1920, los avances en la mecánica cuántica llevaron a que se convirtiera en la formulación estándar para la física atómica. En el verano de 1925, Bohr y Heisenberg publicaron resultados que cerraron la antigua teoría cuántica. Por deferencia a su comportamiento similar a partículas en ciertos procesos y mediciones, los cuantos de luz pasaron a llamarse fotones (1926). En 1926, Erwin Schrödinger sugirió una ecuación diferencial parcial para las funciones de onda de partículas como electrones. Y cuando se restringía efectivamente a una región finita, esta ecuación permitía solo ciertos modos, correspondientes a estados cuánticos discretos, cuyas propiedades resultaron ser exactamente las mismas que las implícitas en la mecánica de la matriz. De la simple postulación de Einstein nació una ráfaga de debates, teorías y pruebas. Por lo tanto, surgió todo el campo de la física cuántica,
Se descubrió que las partículas subatómicas y las ondas electromagnéticas no son simplemente partículas ni ondas, sino que tienen ciertas propiedades de cada una. Esto originó el concepto de dualidad onda-partícula.
Para 1930, la mecánica cuántica se había unificado y formalizado aún más mediante el trabajo de David Hilbert, Paul Dirac y John von Neumann con mayor énfasis en la medición, la naturaleza estadística de nuestro conocimiento de la realidad y la especulación filosófica sobre el "observador". Desde entonces, ha penetrado en muchas disciplinas, incluida la química cuántica, la electrónica cuántica, la óptica cuántica y la ciencia de la información cuántica. Sus desarrollos modernos especulativos incluyen la teoría de cuerdas y las teorías de la gravedad cuántica. También proporciona un marco útil para muchas características de la tabla periódica moderna de elementos, y describe los comportamientos de los átomos durante la unión química y el flujo de electrones en semiconductores de computadora, y por lo tanto juega un papel crucial en muchas tecnologías modernas.
Si bien la mecánica cuántica se construyó para describir el mundo de los muy pequeños, también se necesita para explicar algunos fenómenos macroscópicos como los superconductores y los superfluidos.
La palabra quantum deriva del latín, que significa "qué bien" o "cuánto". En la mecánica cuántica, se refiere a una unidad discreta asignada a ciertas cantidades físicas, como la energía de un átomo en reposo (ver Figura 1). El descubrimiento de que las partículas son paquetes discretos de energía con propiedades ondulatorias condujo a la rama de la física que se ocupa de los sistemas atómicos y subatómicos que hoy se llama mecánica cuántica. Es la base del marco matemático de muchos campos de la física y la química, incluida la física de la materia condensada, física de estado sólido, física atómica, física molecular, física computacional, química computacional, química cuántica, física de partículas, química nuclear y física nuclear. Algunos aspectos fundamentales de la teoría todavía se estudian activamente.
La mecánica cuántica es esencial para comprender el comportamiento de los sistemas a escalas de longitud atómica y menores. Si la naturaleza física de un átomo fuera descrita únicamente por la mecánica clásica, los electrones no orbitarían el núcleo, ya que los electrones en órbita emiten radiación (debido al movimiento circular) y eventualmente colisionarían con el núcleo debido a esta pérdida de energía. Este marco no pudo explicar la estabilidad de los átomos. En cambio, los electrones permanecen en un orbital de onda-partícula probabilístico incierto, no determinista, difuminado y probabilístico alrededor del núcleo, desafiando las suposiciones tradicionales de la mecánica clásica y el electromagnetismo.
La mecánica cuántica se desarrolló inicialmente para proporcionar una mejor explicación y descripción del átomo, especialmente las diferencias en los espectros de luz emitidos por diferentes isótopos del mismo elemento químico, así como partículas subatómicas. En resumen, el modelo atómico de la mecánica cuántica ha tenido un éxito espectacular en el ámbito donde fallan la mecánica clásica y el electromagnetismo.
En términos generales, la mecánica cuántica incorpora cuatro clases de fenómenos que la física clásica no puede explicar:
- cuantificación de ciertas propiedades físicas
- entrelazamiento cuántico
- principio de incertidumbre
- dualidad onda-partícula
Formulaciones matemáticas
En la formulación matemáticamente rigurosa de la mecánica cuántica desarrollada por Paul Dirac, David Hilbert, John von Neumann y Hermann Weyl, los posibles estados de un sistema mecánico cuántico se simbolizan como vectores unitarios (llamados vectores de estado ). Formalmente, estos residen en un espacio de Hilbert separable y complejo, denominado de diversas formas como el espacio de estado o el espacio de Hilbert asociado. del sistema, eso está bien definido hasta un número complejo de la norma 1 (el factor de fase). En otras palabras, los estados posibles son puntos en el espacio proyectivo de un espacio de Hilbert, generalmente llamado el espacio proyectivo complejo. La naturaleza exacta de este espacio de Hilbert depende del sistema; por ejemplo, el espacio de estado para estados de posición e impulso es el espacio de funciones integrables por cuadrados, mientras que el espacio de estado para el giro de un solo protón es solo el producto de dos aviones complejos. Cada observable está representado por un operador lineal máximo hermitiano (precisamente: mediante un autoadjunto) que actúa en el espacio de estado. Cada estado propio de un observable corresponde a un vector propio del operador, y el valor propio asociado corresponde al valor de lo observable en ese estado propio. Si el espectro del operador es discreto,
En el formalismo de la mecánica cuántica, el estado de un sistema en un momento dado se describe mediante una función de onda compleja, también denominada vector de estado en un espacio vectorial complejo. Este objeto matemático abstracto permite el cálculo de probabilidades de resultados de experimentos concretos. Por ejemplo, le permite a uno calcular la probabilidad de encontrar un electrón en una región particular alrededor del núcleo en un momento particular. Contrariamente a la mecánica clásica, nunca se pueden hacer predicciones simultáneas de variables conjugadas, como la posición y el momento, con precisión arbitraria. Por ejemplo, los electrones se pueden considerar (con una cierta probabilidad) ubicados en algún lugar dentro de una región determinada del espacio, pero con sus posiciones exactas desconocidas. Contornos de densidad de probabilidad constante, a menudo denominados "nubes", se puede dibujar alrededor del núcleo de un átomo para conceptualizar dónde se ubicará el electrón con la mayor probabilidad. El principio de incertidumbre de Heisenberg cuantifica la incapacidad para ubicar con precisión la partícula dado su momento conjugado.
De acuerdo con una interpretación, como resultado de una medición, la función de onda que contiene la información de probabilidad para un sistema colapsa desde un estado inicial dado a un estado propio particular. Los posibles resultados de una medición son los valores propios del operador que representan lo observable, lo que explica la elección de los operadores hermitianos , para los cuales todos los valores propios son reales. La distribución de probabilidad de un observable en un estado dado se puede encontrar calculando la descomposición espectral del operador correspondiente. El principio de incertidumbre de Heisenberg está representado por la afirmación de que los operadores correspondientes a ciertos observables no conmutan.
La naturaleza probabilística de la mecánica cuántica proviene, por lo tanto, del acto de medición. Este es uno de los aspectos más difíciles de entender de los sistemas cuánticos. Fue el tema central en los famosos debates de Bohr-Einstein, en el que los dos científicos intentaron aclarar estos principios fundamentales a través de experimentos mentales. En las décadas posteriores a la formulación de la mecánica cuántica, la cuestión de qué constituye una "medida" ha sido ampliamente estudiada. Se han formulado interpretaciones más recientes de la mecánica cuántica que eliminan el concepto de "colapso de la función de onda" (véase, por ejemplo, la interpretación relativa del estado). La idea básica es que cuando un sistema cuántico interactúa con un aparato de medición, sus respectivas funciones de onda se enredan, de modo que el sistema cuántico original deja de existir como una entidad independiente. Para más detalles, consulte el artículo sobre medición en mecánica cuántica.
En general, la mecánica cuántica no asigna valores definidos. En cambio, hace una predicción usando una distribución de probabilidad; es decir, describe la probabilidad de obtener los posibles resultados de la medición de un observable. A menudo, estos resultados están sesgados por muchas causas, como las densas nubes de probabilidad. Las nubes de probabilidad son aproximadas (pero mejores que el modelo de Bohr) por lo que la ubicación de electrones está dada por una función de probabilidad, el eigenvalor de la función de onda, tal que la probabilidad es el módulo cuadrado de la amplitud compleja o atracción statenuclear cuántica. Naturalmente, estas probabilidades dependerán del estado cuántico en el "instante" de la medición. Por lo tanto, la incertidumbre está involucrada en el valor. Sin embargo, hay ciertos estados que están asociados con un valor definido de un observable particular.
En el mundo cotidiano, es natural e intuitivo pensar que todo (todo observable) está en un estado propio. Todo parece tener una posición definida, un impulso definido, una energía definida y un tiempo definido de ocurrencia. Sin embargo, la mecánica cuántica no identifica los valores exactos de la posición y el momento de una partícula (ya que son pares conjugados) o su energía y tiempo (ya que ellos también son pares conjugados). Por el contrario, proporciona solo un rango de probabilidades en el que a esa partícula se le puede dar su impulso y probabilidad de momento. Por lo tanto, es útil usar diferentes palabras para describir estados que tienen valores inciertos y estados que tienen valores definidos (estados propios).
Por lo general, un sistema no estará en un estado propio de la (partícula) observable en la que estamos interesados. Sin embargo, si uno mide lo observable, la función de onda instantáneamente será un estado propio (o estado propio "generalizado") de ese observable. Este proceso se conoce como colapso de la función de onda, un proceso controvertido y muy debatido que implica expandir el sistema en estudio para incluir el dispositivo de medición. Si se conoce la función de onda correspondiente en el instante anterior a la medición, se podrá calcular la probabilidad de que la función de onda colapse en cada uno de los posibles estados propios.
Por ejemplo, la partícula libre en el ejemplo anterior generalmente tendrá una función de onda que es un paquete de onda centrado alrededor de una posición media x 0 (ni un estado propio de posición ni de momento). Cuando uno mide la posición de la partícula, es imposible predecir con certeza el resultado. Es probable, pero no seguro, que estará cerca de x 0 , donde la amplitud de la función de onda es grande. Después de que se realiza la medición, habiendo obtenido algún resultado x , la función de onda colapsa en una posición propia del estado centrada en x .
La evolución temporal de un estado cuántico se describe mediante la ecuación de Schrödinger, en la que el hamiltoniano (el operador correspondiente a la energía total del sistema) genera la evolución del tiempo. La evolución temporal de las funciones de onda es determinista en el sentido de que, dada una función de onda en un momento inicial , hace una predicción definitiva de cuál será la función de onda en cualquier momento posterior .
Durante una medición, por otro lado, el cambio de la función de onda inicial en otra, la función de onda posterior no es determinista, es impredecible (es decir, aleatorio). Aquí se puede ver una simulación de evolución temporal.
Las funciones de onda cambian a medida que avanza el tiempo. La ecuación de Schrödinger describe cómo las funciones de onda cambian en el tiempo, desempeñando un papel similar a la segunda ley de Newton en la mecánica clásica. La ecuación de Schrödinger, aplicada al ejemplo antes mencionado de la partícula libre, predice que el centro de un paquete de ondas se moverá a través del espacio a una velocidad constante (como una partícula clásica sin fuerzas que actúen sobre ella). Sin embargo, el paquete de ondas también se extenderá a medida que avance el tiempo, lo que significa que la posición se vuelve más incierta con el tiempo. Esto también tiene el efecto de convertir un estado propio de posición (que puede considerarse como un paquete de onda infinitamente agudo) en un paquete de onda ampliado que ya no representa un estado propio de posición (definido, cierto).
Algunas funciones de onda producen distribuciones de probabilidad que son constantes o independientes del tiempo, como cuando en un estado estacionario de energía constante, el tiempo desaparece en el cuadrado absoluto de la función de onda. Muchos sistemas que se tratan dinámicamente en mecánica clásica se describen mediante funciones de onda "estáticas". Por ejemplo, un solo electrón en un átomo no excitado se representa clásicamente como una partícula que se mueve en una trayectoria circular alrededor del núcleo atómico, mientras que en la mecánica cuántica se describe mediante una función de onda estática esféricamente simétrica que rodea el núcleo (Fig. 1) ( tenga en cuenta, sin embargo, que solo los estados de momento angular más bajo, etiquetados como s , son esféricamente simétricos).
La ecuación de Schrödinger actúa sobre la amplitud de probabilidad completa , no simplemente su valor absoluto. Mientras que el valor absoluto de la amplitud de probabilidad codifica información sobre probabilidades, su fase codifica información sobre la interferencia entre estados cuánticos. Esto da lugar al comportamiento "ondulatorio" de los estados cuánticos. Resulta que las soluciones analíticas de la ecuación de Schrödinger están disponibles solo para un número muy pequeño de Hamiltonianos modelo relativamente simples, de los cuales el oscilador armónico cuántico, la partícula en una caja, el catión dihidrógeno y el átomo de hidrógeno son los más importantes. representantes. Incluso el átomo de helio, que contiene solo un electrón más que el átomo de hidrógeno, ha desafiado todos los intentos de un tratamiento totalmente analítico.
Sin embargo, existen varias técnicas para generar soluciones aproximadas. En el importante método conocido como teoría de la perturbación, se usa el resultado analítico de un modelo mecánico cuántico simple para generar un resultado para un modelo más complicado que se relaciona con el modelo más simple mediante (por ejemplo) la adición de una energía potencial débil. Otro método es el enfoque de "ecuación semiclásica del movimiento", que se aplica a los sistemas para los cuales la mecánica cuántica produce solo desviaciones débiles (pequeñas) del comportamiento clásico. Estas desviaciones se pueden calcular a partir del movimiento clásico. Este enfoque es particularmente importante en el campo del caos cuántico.
Formulaciones matemáticamente equivalentes de mecánica cuántica
Existen numerosas formulaciones matemáticamente equivalentes de mecánica cuántica. Una de las formulaciones más antiguas y usadas es la "teoría de la transformación" propuesta por Paul Dirac, que unifica y generaliza las dos primeras formulaciones de la mecánica cuántica: la mecánica de matrices (inventada por Werner Heisenberg) y la mecánica ondulatoria (inventada por Erwin Schrödinger).
Especialmente desde que Werner Heisenberg fue galardonado con el Premio Nobel de Física en 1932 por la creación de la mecánica cuántica, el papel de Max Born en el desarrollo de QM se pasó por alto hasta el Premio Nobel de 1954. El papel se observa en una biografía de Born de 2005, que relata su papel en la formulación matricial de la mecánica cuántica y el uso de amplitudes probabilísticas. El propio Heisenberg reconoce haber aprendido matrices del Born, tal como se publicó en un festschrift de 1940 honrando a Max Planck. En la formulación de la matriz, el estado instantáneo de un sistema cuántico codifica las probabilidades de sus propiedades medibles, o "observables". Los ejemplos de observables incluyen energía, posición, momento y momento angular. Los observables pueden ser continuos (por ejemplo, la posición de una partícula) o discretos (por ejemplo, la energía de un electrón unido a un átomo de hidrógeno). Una formulación alternativa de la mecánica cuántica es la formulación integral de la trayectoria de Feynman, en la que se considera una amplitud mecánica cuántica como una suma sobre todos los caminos posibles clásicos y no clásicos entre los estados inicial y final. Este es el equivalente cuántico mecánico del principio de acción en la mecánica clásica.
Interacciones con otras teorías científicas
Las reglas de la mecánica cuántica son fundamentales. Afirman que el espacio de estado de un sistema es un espacio de Hilbert (crucialmente, que el espacio tiene un producto interno) y que los observables de ese sistema son operadores hermitianos que actúan sobre vectores en ese espacio, aunque no nos dicen en qué espacio de Hilbert o cuales operadores Estos pueden ser elegidos apropiadamente para obtener una descripción cuantitativa de un sistema cuántico. Una guía importante para tomar estas decisiones es el principio de correspondencia, que establece que las predicciones de la mecánica cuántica se reducen a las de la mecánica clásica cuando un sistema se mueve a energías más altas o, equivalentemente, a números cuánticos más grandes, es decir, una sola partícula exhibe un grado de la aleatoriedad, en sistemas que incorporan millones de partículas, toma el promedio y, en el límite de alta energía, la probabilidad estadística de comportamiento aleatorio se aproxima a cero. En otras palabras, la mecánica clásica es simplemente una mecánica cuántica de sistemas grandes. Este límite de "alta energía" se conoce como el límite clásico o por correspondencia . Incluso se puede partir de un modelo clásico establecido de un sistema particular, luego intentar adivinar el modelo cuántico subyacente que daría lugar al modelo clásico en el límite de correspondencia.
| Problema sin resolver en física : En el límite de correspondencia de la mecánica cuántica : ¿hay una interpretación preferida de la mecánica cuántica? ¿De qué manera la descripción cuántica de la realidad, que incluye elementos como la "superposición de estados" y la "función de las olas colapsan", da lugar a la realidad que percibimos? (más problemas sin resolver en física) |
Cuando la mecánica cuántica se formuló originalmente, se aplicó a modelos cuyo límite de correspondencia era la mecánica clásica no relativista. Por ejemplo, el modelo bien conocido del oscilador armónico cuántico utiliza una expresión explícitamente no relativista para la energía cinética del oscilador, y es así una versión cuántica del oscilador armónico clásico.
Los primeros intentos de fusionar la mecánica cuántica con la relatividad especial implicaron el reemplazo de la ecuación de Schrödinger por una ecuación covariante como la ecuación de Klein-Gordon o la ecuación de Dirac. Si bien estas teorías tuvieron éxito al explicar muchos resultados experimentales, tenían ciertas cualidades insatisfactorias derivadas de su descuido de la creación relativista y la aniquilación de partículas. Una teoría cuántica completamente relativista requirió el desarrollo de la teoría cuántica de campos, que aplica la cuantificación a un campo (en lugar de un conjunto fijo de partículas). La primera teoría de campos cuánticos completa, la electrodinámica cuántica, proporciona una descripción completamente cuántica de la interacción electromagnética. El aparato completo de la teoría cuántica de campos a menudo es innecesario para describir sistemas electrodinámicos. Un enfoque más simple, uno que se ha empleado desde el inicio de la mecánica cuántica, es tratar las partículas cargadas como objetos mecánicos cuánticos sobre los que actúa un campo electromagnético clásico. Por ejemplo, el modelo cuántico elemental del átomo de hidrógeno describe el campo eléctrico del átomo de hidrógeno usando un clásico Potencial de culombio Este enfoque "semiclásico" falla si las fluctuaciones cuánticas en el campo electromagnético juegan un papel importante, como en la emisión de fotones por partículas cargadas.
Las teorías cuánticas de campo para la fuerza nuclear fuerte y la fuerza nuclear débil también se han desarrollado. La teoría del campo cuántico de la fuerza nuclear fuerte se llama cromodinámica cuántica y describe las interacciones de partículas subnucleares como los quarks y los gluones. La fuerza nuclear débil y la fuerza electromagnética se unificaron, en sus formas cuantificadas, en una sola teoría cuántica de campo (conocida como teoría electrodébil), por los físicos Abdus Salam, Sheldon Glashow y Steven Weinberg. Estos tres hombres compartieron el Premio Nobel de Física en 1979 por este trabajo.
Ha resultado difícil construir modelos cuánticos de gravedad, la fuerza fundamental restante. Las aproximaciones semiclásicas son factibles y han dado lugar a predicciones como la radiación de Hawking. Sin embargo, la formulación de una teoría completa de la gravedad cuántica se ve obstaculizada por aparentes incompatibilidades entre la relatividad general (la teoría de la gravedad más precisa actualmente conocida) y algunos de los supuestos fundamentales de la teoría cuántica. La resolución de estas incompatibilidades es un área de investigación activa, y teorías como la teoría de cuerdas se encuentran entre los posibles candidatos para una teoría futura de la gravedad cuántica.
La mecánica clásica también se ha extendido al dominio complejo, con una mecánica clásica compleja que exhibe comportamientos similares a la mecánica cuántica.
Mecánica cuántica y física clásica
Las predicciones de la mecánica cuántica se han verificado experimentalmente con un alto grado de precisión. De acuerdo con el principio de correspondencia entre mecánica clásica y cuántica, todos los objetos obedecen las leyes de la mecánica cuántica, y la mecánica clásica es solo una aproximación para grandes sistemas de objetos (o una mecánica cuántica estadística de una gran colección de partículas). Las leyes de la mecánica clásica se derivan de las leyes de la mecánica cuántica como un promedio estadístico al límite de sistemas grandes o grandes números cuánticos. Sin embargo, los sistemas caóticos no tienen buenos números cuánticos, y el caos cuántico estudia la relación entre descripciones clásicas y cuánticas. en estos sistemas.
La coherencia cuántica es una diferencia esencial entre teorías clásicas y cuánticas, como lo ilustra la paradoja de Einstein-Podolsky-Rosen (EPR): un ataque a una determinada interpretación filosófica de la mecánica cuántica mediante un llamamiento al realismo local. La interferencia cuántica implica sumar amplitudes de probabilidad , mientras que las "ondas" clásicas infieren que existe una suma de intensidades. Para cuerpos microscópicos, la extensión del sistema es mucho más pequeña que la longitud de coherencia, lo que da lugar a un enredo de largo alcance y otros fenómenos no locales característicos de los sistemas cuánticos. La coherencia cuántica no es típicamente evidente a escalas macroscópicas, aunque una excepción a esta regla puede ocurrir a temperaturas extremadamente bajas (es decir, acercándose al cero absoluto) en las que el comportamiento cuántico puede manifestarse macroscópicamente. Esto está de acuerdo con las siguientes observaciones:
- Muchas propiedades macroscópicas de un sistema clásico son una consecuencia directa del comportamiento cuántico de sus partes. Por ejemplo, la estabilidad de la materia a granel (que consiste en átomos y moléculas que colapsarían rápidamente bajo fuerzas eléctricas solamente), la rigidez de los sólidos y las propiedades mecánicas, térmicas, químicas, ópticas y magnéticas de la materia son todos resultados de la interacción de cargas eléctricas bajo las reglas de la mecánica cuántica.
- Mientras que el comportamiento aparentemente "exótico" de la materia planteada por la mecánica cuántica y la teoría de la relatividad se vuelven más evidentes cuando se trata de partículas de tamaño extremadamente pequeño o velocidades que se aproximan a la velocidad de la luz, las leyes de la física clásica, a menudo considerada "newtoniana" predecir el comportamiento de la gran mayoría de los objetos "grandes" (del orden del tamaño de las moléculas grandes o más grandes) a velocidades mucho más pequeñas que la velocidad de la luz.
Interpretación de Copenhague de la cinemática cuántica frente a la clásica
Una gran diferencia entre la mecánica clásica y la cuántica es que usan descripciones cinemáticas muy diferentes.
En la visión madura de Niels Bohr, los fenómenos mecánicos cuánticos son necesarios para experimentos, con descripciones completas de todos los dispositivos para el sistema, preparativos, intermediarios y, finalmente, medición. Las descripciones están en términos macroscópicos, expresadas en lenguaje ordinario, complementadas con los conceptos de mecánica clásica. La condición inicial y la condición final del sistema se describen respectivamente por valores en un espacio de configuración, por ejemplo, un espacio de posición, o algún espacio equivalente, como un espacio de momento. La mecánica cuántica no admite una descripción completamente precisa, en términos tanto de posición como de momento, de una condición inicial o "estado" (en el sentido clásico de la palabra) que respaldaría una predicción determinista y causal precisa de una condición final. En este sentido, defendido por Bohr en sus escritos maduros, un fenómeno cuántico es un proceso, un paso de la condición inicial a la final, no un "estado" instantáneo en el sentido clásico de esa palabra. Por lo tanto, hay dos tipos de procesos en la mecánica cuántica: estacionario y de transición. Para un proceso estacionario, la condición inicial y final es la misma. Para una transición, son diferentes. Obviamente, por definición, si solo se da la condición inicial, el proceso no está determinado. Dada su condición inicial, la predicción de su condición final es posible, causalmente pero solo de manera probabilística, porque la ecuación de Schrödinger es determinista para la evolución de la función de onda, pero la función de onda describe el sistema solo de forma probabilística. no es un "estado" instantáneo en el sentido clásico de esa palabra. Por lo tanto, hay dos tipos de procesos en la mecánica cuántica: estacionario y de transición. Para un proceso estacionario, la condición inicial y final es la misma. Para una transición, son diferentes. Obviamente, por definición, si solo se da la condición inicial, el proceso no está determinado. Dada su condición inicial, la predicción de su condición final es posible, causalmente pero solo de manera probabilística, porque la ecuación de Schrödinger es determinista para la evolución de la función de onda, pero la función de onda describe el sistema solo de forma probabilística. no es un "estado" instantáneo en el sentido clásico de esa palabra. Por lo tanto, hay dos tipos de procesos en la mecánica cuántica: estacionario y de transición. Para un proceso estacionario, la condición inicial y final es la misma. Para una transición, son diferentes. Obviamente, por definición, si solo se da la condición inicial, el proceso no está determinado. Dada su condición inicial, la predicción de su condición final es posible, causalmente pero solo de manera probabilística, porque la ecuación de Schrödinger es determinista para la evolución de la función de onda, pero la función de onda describe el sistema solo de forma probabilística. Para una transición, son diferentes. Obviamente, por definición, si solo se da la condición inicial, el proceso no está determinado. Dada su condición inicial, la predicción de su condición final es posible, causalmente pero solo de manera probabilística, porque la ecuación de Schrödinger es determinista para la evolución de la función de onda, pero la función de onda describe el sistema solo de forma probabilística. Para una transición, son diferentes. Obviamente, por definición, si solo se da la condición inicial, el proceso no está determinado. Dada su condición inicial, la predicción de su condición final es posible, causalmente pero solo de manera probabilística, porque la ecuación de Schrödinger es determinista para la evolución de la función de onda, pero la función de onda describe el sistema solo de forma probabilística.
Para muchos experimentos, es posible pensar en las condiciones iniciales y finales del sistema como una partícula. En algunos casos, parece que hay potencialmente varias rutas o trayectorias espacialmente distintas por las que una partícula podría pasar de la condición inicial a la final. Es una característica importante de la descripción de la cinemática cuántica que no permite una declaración definida única de cuál de esas vías se sigue realmente. Solo las condiciones iniciales y finales son definitivas y, tal como se establece en el párrafo anterior, se definen solo con la precisión que permite la descripción del espacio de configuración o su equivalente. En todos los casos para los que se necesita una descripción cinemática cuántica, siempre hay una razón de peso para esta restricción de precisión cinemática. Un ejemplo de tal razón es que para que una partícula se encuentre experimentalmente en una posición definida, debe mantenerse inmóvil; para que se descubra experimentalmente que tiene un impulso definido, debe tener movimiento libre; estos dos son lógicamente incompatibles.
La cinemática clásica no exige principalmente una descripción experimental de sus fenómenos. Permite la descripción completamente precisa de un estado instantáneo por un valor en el espacio de fase, el producto cartesiano de la configuración y los espacios de momento. Esta descripción simplemente asume o imagina un estado como una entidad físicamente existente sin preocuparse por su mensurabilidad experimental. Tal descripción de una condición inicial, junto con las leyes del movimiento de Newton, permite una predicción determinista y causal precisa de una condición final, con una trayectoria definida de paso. La dinámica de Hamilton se puede usar para esto. La cinemática clásica también permite la descripción de un proceso análogo a la descripción de la condición inicial y final utilizada por la mecánica cuántica. La mecánica de Lagrange se aplica a esto. Para procesos que necesitan tener en cuenta las acciones de un pequeño número de constantes de Planck, la cinemática clásica no es adecuada; la mecánica cuántica es necesaria.
Relatividad general y mecánica cuántica
Incluso con los postulados definitorios de la teoría de la relatividad general y de la teoría cuántica de Einstein que están indiscutiblemente respaldados por evidencia empírica rigurosa y repetida, y aunque no se contradicen directamente entre sí teóricamente (al menos con respecto a sus afirmaciones principales), han demostrado extremadamente difícil de incorporar en un modelo consistente y cohesivo.
La gravedad es insignificante en muchas áreas de la física de partículas, por lo que la unificación entre la relatividad general y la mecánica cuántica no es un problema urgente en esas aplicaciones particulares. Sin embargo, la falta de una teoría correcta de la gravedad cuántica es un tema importante en la cosmología física y la búsqueda por parte de los físicos de una elegante "teoría de todo" (TOE). En consecuencia, resolver las incoherencias entre ambas teorías ha sido un objetivo principal de la física de los siglos 20 y 21. Muchos físicos prominentes, incluido Stephen Hawking, han trabajado durante muchos años en el intento de descubrir una teoría que subyace a todo. Este TOE combinaría no solo los diferentes modelos de física subatómica, sino que también derivaría las cuatro fuerzas fundamentales de la naturaleza -la fuerza fuerte, el electromagnetismo, la fuerza débil y la gravedad- de una sola fuerza o fenómeno. Mientras Stephen Hawking era inicialmente un creyente en la Teoría del Todo, después de considerar el Teorema de Incompletitud de Gödel, ha concluido que no se puede obtener, y lo ha declarado públicamente en su conferencia "Gödel y el Fin de la Física" (2002).
Intentos de una teoría de campo unificada
La búsqueda de unificar las fuerzas fundamentales a través de la mecánica cuántica todavía está en curso. La electrodinámica cuántica (o "electromagnetismo cuántico"), que actualmente (al menos en el régimen de perturbaciones) es la teoría física probada con mayor precisión en competencia con la relatividad general, se fusionó con la fuerza nuclear débil en la fuerza electrodébil y actualmente se está trabajando hecho para combinar la fuerza electrodébil y fuerte en la fuerza electrostrong. Las predicciones actuales afirman que alrededor de 10 GeV las tres fuerzas antes mencionadas se fusionan en un solo campo unificado. Más allá de esta "gran unificación", se especula que es posible fusionar la gravedad con las otras tres simetrías de gauge, que se espera que ocurran a aproximadamente 10 GeV. Sin embargo, y aunque la relatividad especial se incorpora parsimoniosamente en la electrodinámica cuántica, la relatividad general expandida, actualmente la mejor teoría que describe la fuerza de la gravedad, no se ha incorporado completamente en la teoría cuántica. Uno de los que buscan un TOE coherente es Edward Witten, un físico teórico que formuló la teoría M, que es un intento de describir la teoría de cuerdas supersimétrica. La teoría M postula que nuestro espacio-tiempo 4-dimensional aparente es, en realidad, un espacio-tiempo de 11 dimensiones que contiene 10 dimensiones espaciales y 1 dimensión temporal, aunque 7 de las dimensiones espaciales son, a energías inferiores, completamente "compactadas" (o infinitamente curvado) y no fácilmente susceptible de medición o sondeo. actualmente, la mejor teoría que describe la fuerza de la gravedad, no se ha incorporado completamente en la teoría cuántica. Uno de los que buscan un TOE coherente es Edward Witten, un físico teórico que formuló la teoría M, que es un intento de describir la teoría de cuerdas supersimétrica. La teoría M postula que nuestro espacio-tiempo 4-dimensional aparente es, en realidad, un espacio-tiempo de 11 dimensiones que contiene 10 dimensiones espaciales y 1 dimensión temporal, aunque 7 de las dimensiones espaciales son, a energías inferiores, completamente "compactadas" (o infinitamente curvado) y no fácilmente susceptible de medición o sondeo. actualmente, la mejor teoría que describe la fuerza de la gravedad, no se ha incorporado completamente en la teoría cuántica. Uno de los que buscan un TOE coherente es Edward Witten, un físico teórico que formuló la teoría M, que es un intento de describir la teoría de cuerdas supersimétrica. La teoría M postula que nuestro espacio-tiempo 4-dimensional aparente es, en realidad, un espacio-tiempo de 11 dimensiones que contiene 10 dimensiones espaciales y 1 dimensión temporal, aunque 7 de las dimensiones espaciales son, a energías inferiores, completamente "compactadas" (o infinitamente curvado) y no fácilmente susceptible de medición o sondeo. que es un intento de describir la teoría de cuerdas supersimétrica basada. La teoría M postula que nuestro espacio-tiempo 4-dimensional aparente es, en realidad, un espacio-tiempo de 11 dimensiones que contiene 10 dimensiones espaciales y 1 dimensión temporal, aunque 7 de las dimensiones espaciales son, a energías inferiores, completamente "compactadas" (o infinitamente curvado) y no fácilmente susceptible de medición o sondeo. que es un intento de describir la teoría de cuerdas supersimétrica basada. La teoría M postula que nuestro espacio-tiempo 4-dimensional aparente es, en realidad, un espacio-tiempo de 11 dimensiones que contiene 10 dimensiones espaciales y 1 dimensión temporal, aunque 7 de las dimensiones espaciales son, a energías inferiores, completamente "compactadas" (o infinitamente curvado) y no fácilmente susceptible de medición o sondeo.
Otra teoría popular es la gravedad cuántica de lazo (LQG), una teoría propuesta por primera vez por Carlo Rovelli que describe las propiedades cuánticas de la gravedad. También es una teoría del espacio cuántico y del tiempo cuántico, porque en la relatividad general, la geometría del espaciotiempo es una manifestación de la gravedad. LQG es un intento de fusionar y adaptar la mecánica cuántica estándar y la relatividad general estándar. El resultado principal de la teoría es una imagen física del espacio donde el espacio es granular. La granularidad es una consecuencia directa de la cuantificación. Tiene la misma naturaleza de la granularidad de los fotones en la teoría cuántica del electromagnetismo o los niveles discretos de la energía de los átomos. Pero aquí está el espacio en sí, que es discreto. Más precisamente, el espacio puede verse como un tejido extremadamente fino o una red "tejida" de bucles finitos. Estas redes de bucles se llaman redes spin. La evolución de una red de espín a lo largo del tiempo se llama espuma de espín. El tamaño predicho de esta estructura es la longitud de Planck, que es aproximadamente 1.616 × 10 m. De acuerdo con la teoría, no hay ningún significado para la longitud más corta que esto (véase la energía de la escala de Planck). Por lo tanto, LQG predice que no solo la materia, sino también el espacio mismo, tiene una estructura atómica.
Implicaciones filosóficas
Desde su inicio, los muchos aspectos y resultados contraintuitivos de la mecánica cuántica han provocado fuertes debates filosóficos y muchas interpretaciones. Incluso cuestiones fundamentales, como las reglas básicas de Max Born sobre amplitudes de probabilidad y distribuciones de probabilidad, tardaron décadas en ser apreciadas por la sociedad y muchos científicos destacados. Richard Feynman dijo una vez: "Creo que puedo decir con seguridad que nadie entiende la mecánica cuántica". Según Steven Weinberg, "ahora, en mi opinión, no hay una interpretación totalmente satisfactoria de la mecánica cuántica".
La interpretación de Copenhague, debido en gran parte a Niels Bohr y Werner Heisenberg, sigue siendo la más aceptada entre los físicos, unos 75 años después de su enunciación. De acuerdo con esta interpretación, la naturaleza probabilística de la mecánica cuántica no es una característica temporal que eventualmente será reemplazada por una teoría determinista, sino que debe ser considerada como una renuncia final a la idea clásica de "causalidad". También se cree que cualquier aplicación bien definida del formalismo mecánico cuántico siempre debe hacer referencia a la disposición experimental, debido a la naturaleza conjugada de la evidencia obtenida en diferentes situaciones experimentales.
Albert Einstein, uno de los fundadores de la teoría cuántica, no aceptó algunas de las interpretaciones más filosóficas o metafísicas de la mecánica cuántica, como el rechazo del determinismo y de la causalidad. Es célebremente citado diciendo que, en respuesta a este aspecto, "Dios no juega con los dados". Rechazó el concepto de que el estado de un sistema físico depende de la disposición experimental para su medición. Sostuvo que un estado de naturaleza ocurre por derecho propio, independientemente de si se observa o no. Desde ese punto de vista, él está respaldado por la definición actualmente aceptada de un estado cuántico, que permanece invariable bajo la elección arbitraria del espacio de configuración para su representación, es decir, modo de observación. También sostuvo que la mecánica cuántica subyacente debería ser una teoría que expresa completa y directamente la regla contra la acción a distancia; en otras palabras, insistió en el principio de localidad. Consideró, pero rechazó por razones teóricas, una propuesta particular de variables ocultas para obviar el indeterminismo o acausalidad de la medición de la mecánica cuántica. Consideró que la mecánica cuántica era una teoría actualmente válida, pero no definitiva para los fenómenos cuánticos. Pensó que su reemplazo en el futuro requeriría profundos avances conceptuales, y que no llegaría de manera rápida o fácil. Los debates de Bohr-Einstein proporcionan una crítica vibrante de la Interpretación de Copenhague desde un punto de vista epistemológico. Al defender sus puntos de vista, presentó una serie de objeciones,
John Bell demostró que esta paradoja EPR llevó a diferencias experimentalmente comprobables entre la mecánica cuántica y las teorías que se basan en las variables ocultas adicionales. Se han realizado experimentos que confirman la precisión de la mecánica cuántica, lo que demuestra que la mecánica cuántica no puede mejorarse mediante la adición de variables ocultas. Los experimentos iniciales de Alain Aspect en 1982, y muchos experimentos posteriores desde entonces, han verificado definitivamente el enredo cuántico. A principios de los años ochenta, los experimentos habían demostrado que tales desigualdades efectivamente se violaban en la práctica, de modo que en realidad había correlaciones del tipo sugerido por la mecánica cuántica. Al principio, parecían efectos esotéricos aislados, pero a mediados de la década de 1990 se codificaron en el campo de la teoría de la información cuántica.
El enredo, como se demostró en los experimentos tipo Bell, no viola la causalidad, ya que no ocurre transferencia de información. El enredo cuántico forma la base de la criptografía cuántica, que se propone para su uso en aplicaciones comerciales de alta seguridad en banca y gobierno.
La interpretación de muchos mundos de Everett, formulada en 1956, sostiene que todas las posibilidades descritas por la teoría cuántica ocurren simultáneamente en un multiverso compuesto por universos paralelos mayoritariamente independientes. Esto no se logra introduciendo un "nuevo axioma" para la mecánica cuántica, sino por el contrario, eliminando el axioma del colapso del paquete de ondas. Todos los posibles estados consistentes del sistema medido y el aparato de medición (incluido el observador) están presentes en un real físico, no solo formalmente matemático, como en otras interpretaciones, superposición cuántica. Tal superposición de combinaciones de estado consistentes de diferentes sistemas se llama un estado enredado. Mientras que el multiverso es determinista, percibimos un comportamiento no determinista gobernado por probabilidades, porque solo podemos observar el universo (es decir, la contribución consistente del estado a la superposición antes mencionada) que nosotros, como observadores, habitamos. La interpretación de Everett es perfectamente consistente con los experimentos de John Bell y los hace intuitivamente comprensibles. Sin embargo, de acuerdo con la teoría de la decoherencia cuántica, estos "universos paralelos" nunca serán accesibles para nosotros. La inaccesibilidad se puede entender de la siguiente manera: una vez que se realiza una medición, el sistema medido se enreda con ambos el físico que lo midió y una gran cantidad de otras partículas, algunas de las cuales son fotones volando a la velocidad de la luz hacia el otro extremo del universo. Para demostrar que la función de onda no colapsó, uno tendría que recuperar todas estas partículas y medirlas de nuevo, junto con el sistema que se midió originalmente. Esto no es completamente práctico, pero incluso si uno pudiera teóricamente hacer esto, tendría que destruir cualquier evidencia de que la medición original tuvo lugar (incluida la memoria del físico). A la luz de estas pruebas de Bell, Cramer (1986) formuló su interpretación transaccional que es única al proporcionar una explicación física de la regla de Born. La mecánica cuántica relacional apareció a finales de la década de 1990 como la derivada moderna de la Interpretación de Copenhague.
Aplicaciones
La mecánica cuántica ha tenido un enorme éxito al explicar muchas de las características de nuestro universo. La mecánica cuántica es a menudo la única teoría que puede revelar los comportamientos individuales de las partículas subatómicas que componen todas las formas de la materia (electrones, protones, neutrones, fotones y otros). La mecánica cuántica ha influido fuertemente en las teorías de cuerdas, candidatas a una Teoría del Todo (ver reduccionismo).
La mecánica cuántica también es críticamente importante para comprender cómo se unen los átomos individuales mediante un enlace covalente para formar moléculas. La aplicación de la mecánica cuántica a la química se conoce como química cuántica. La mecánica cuántica también puede proporcionar una visión cuantitativa de los procesos de enlace iónico y covalente al mostrar explícitamente qué moléculas son energéticamente favorables a las otras y las magnitudes de las energías involucradas. Además, la mayoría de los cálculos realizados en la química computacional moderna se basan en la mecánica cuántica.
En muchos aspectos, la tecnología moderna opera a una escala donde los efectos cuánticos son significativos.
Electrónica
Muchos dispositivos electrónicos modernos están diseñados con mecánica cuántica. Los ejemplos incluyen el láser, el transistor (y por lo tanto el microchip), el microscopio electrónico y la resonancia magnética (MRI). El estudio de los semiconductores condujo a la invención del diodo y el transistor, que son partes indispensables de los sistemas modernos de electrónica, computadoras y dispositivos de telecomunicación. Otra aplicación es para fabricar diodos láser y diodos emisores de luz, que son una fuente de luz de alta eficiencia.
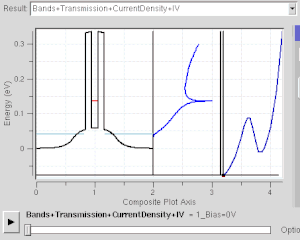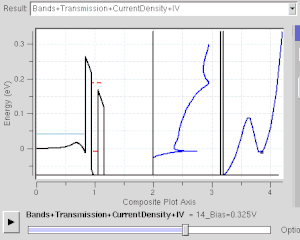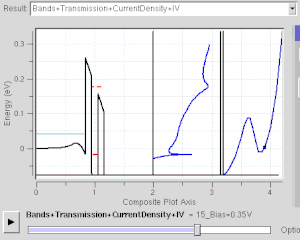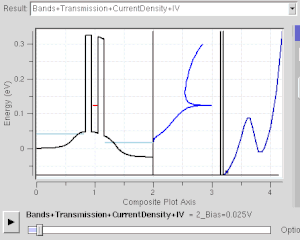
Muchos dispositivos electrónicos funcionan bajo el efecto del túnel cuántico. Incluso existe en el interruptor de luz simple. El interruptor no funcionaría si los electrones no pudieran hacer un túnel cuántico a través de la capa de oxidación en las superficies de contacto del metal. Los chips de memoria flash que se encuentran en las unidades USB utilizan el túnel cuántico para borrar sus celdas de memoria. Algunos dispositivos de resistencia diferencial negativa también utilizan el efecto de efecto túnel cuántico, como el diodo túnel resonante. A diferencia de los diodos clásicos, su corriente se transmite mediante un túnel resonante a través de dos o más barreras potenciales (ver figura derecha). Su comportamiento de resistencia negativa solo puede entenderse con la mecánica cuántica: a medida que el estado confinado se acerca al nivel de Fermi, la corriente del túnel aumenta. A medida que se aleja, la corriente disminuye. La mecánica cuántica es necesaria para comprender y diseñar dichos dispositivos electrónicos.
Criptografía
Los investigadores actualmente están buscando métodos sólidos para manipular directamente estados cuánticos. Se están realizando esfuerzos para desarrollar de forma más completa la criptografía cuántica, que teóricamente permitirá la transmisión de información garantizada y segura.
Una ventaja inherente producida por la criptografía cuántica en comparación con la criptografía clásica es la detección de escuchas pasivas. Este es un resultado natural del comportamiento de los bits cuánticos; debido al efecto del observador, si se observara un bit en un estado de superposición, el estado de superposición colapsaría en un estado propio. Debido a que el destinatario previsto esperaba recibir el bit en un estado de superposición, el destinatario previsto sabría que hubo un ataque, porque el estado del bit ya no estaría en una superposición.
Computación cuántica
Otro objetivo es el desarrollo de computadoras cuánticas, que se espera que realicen ciertas tareas computacionales de forma exponencialmente más rápida que las computadoras clásicas. En lugar de utilizar bits clásicos, las computadoras cuánticas usan qubits, que pueden estar en superposiciones de estados. Los programadores cuánticos pueden manipular la superposición de qubits para resolver problemas que la informática clásica no puede hacer de manera efectiva, como buscar bases de datos sin clasificar o factorizar enteros. IBM afirma que el advenimiento de la computación cuántica puede avanzar en los campos de la medicina, la logística, los servicios financieros, la inteligencia artificial y la seguridad en la nube.
Otro tema de investigación activo es la teleportación cuántica, que trata de técnicas para transmitir información cuántica a distancias arbitrarias.
Efectos cuánticos a escala macroscópica
Si bien la mecánica cuántica se aplica principalmente a los regímenes atómicos más pequeños de la materia y la energía, algunos sistemas muestran efectos mecánicos cuánticos a gran escala. La superfluidez, el flujo sin fricción de un líquido a temperaturas cercanas al cero absoluto, es un ejemplo bien conocido. También lo es el fenómeno estrechamente relacionado de la superconductividad, el flujo sin fricción de un gas de electrones en un material conductor (una corriente eléctrica) a temperaturas suficientemente bajas. El efecto Hall cuántico fraccionario es un estado ordenado topológico que corresponde a patrones de enredo cuántico de largo alcance. Los estados con diferentes órdenes topológicos (o diferentes patrones de enredos de largo alcance) no pueden cambiarse entre sí sin una transición de fase.
Teoría cuántica
La teoría cuántica también proporciona descripciones precisas para muchos fenómenos previamente inexplicados, como la radiación del cuerpo negro y la estabilidad de los orbitales de los electrones en los átomos. También ha dado una idea del funcionamiento de muchos sistemas biológicos diferentes, incluidos los receptores de olores y las estructuras de proteínas. El trabajo reciente sobre la fotosíntesis ha proporcionado evidencia de que las correlaciones cuánticas juegan un papel esencial en este proceso fundamental de las plantas y muchos otros organismos. Aun así, la física clásica a menudo puede proporcionar buenas aproximaciones a los resultados obtenidos de otra manera por la física cuántica, típicamente en circunstancias con un gran número de partículas o grandes números cuánticos. Dado que las fórmulas clásicas son mucho más simples y fáciles de calcular que las fórmulas cuánticas,
Ejemplos
Partícula libre
Por ejemplo, considera una partícula libre. En la mecánica cuántica, una materia libre se describe mediante una función de onda. Las propiedades de las partículas de la materia se vuelven aparentes cuando medimos su posición y velocidad. Las propiedades de onda de la materia se vuelven aparentes cuando medimos sus propiedades de onda como la interferencia. La característica de dualidad onda-partícula se incorpora en las relaciones de coordenadas y operadores en la formulación de la mecánica cuántica. Como el asunto es libre (no está sujeto a ninguna interacción), su estado cuántico se puede representar como una onda de forma arbitraria y se extiende sobre el espacio como una función de onda. La posición y el momento de la partícula son observables. El Principio de Incertidumbre establece que tanto la posición como el momento no se pueden medir simultáneamente con total precisión. Sin embargo, uno puede mida la posición (solo) de una partícula libre en movimiento, creando un estado propio de posición con una función de onda que es muy grande (un delta Dirac) en una posición particular x , y cero en cualquier otro lugar. Si se realiza una medición de posición en dicha función de onda, la x resultante se obtendrá con 100% de probabilidad (es decir, con total certeza o precisión completa). Esto se llama un estado propio de posición o, dicho en términos matemáticos, un estado propio de posición generalizada (eigendistribución). Si la partícula está en un estado propio de posición, entonces su momento es completamente desconocido. Por otro lado, si la partícula está en un estado propio de momento, entonces su posición es completamente desconocida. En un estado propio de momento que tiene una forma de onda plana, se puede demostrar que la longitud de onda es igual a h / p , donde h es la constante de Planck y p es el momento del estado propio.
Partícula en una caja
La partícula en una caja de energía potencial unidimensional es el ejemplo más matemáticamente simple donde las restricciones conducen a la cuantificación de los niveles de energía. La caja se define como que tiene energía potencial cero en todas partes dentro de una región determinada y, por lo tanto, energía potencial infinita fuera de esa región. Para el caso unidimensional en la dirección, se puede escribir la ecuación de Schrödinger independiente del tiempo
Con el operador diferencial definido por
la ecuación anterior evoca el análogo clásico de la energía cinética,
con estado en este caso que tiene energía coincidente con la energía cinética de la partícula.
Las soluciones generales de la ecuación de Schrödinger para la partícula en una caja son
o, de la fórmula de Euler,
Las paredes potenciales infinitos de la caja de determinar los valores de C , D , y k en x = 0 y x = L donde ψ debe ser cero. Por lo tanto, en x = 0 ,
y D = 0 . En x = L ,
en el cual C no puede ser cero ya que esto entraría en conflicto con la interpretación de Born. Por lo tanto, dado que sin ( kL ) = 0 , kL debe ser un múltiplo entero de π,
La cuantificación de los niveles de energía se sigue de esta restricción en k , ya que
- La energía de estado fundamental de las partículas es E 1 para n = 1.
- La energía de la partícula en el estado n es E n = nE 1 , n = 2,3,4, .....
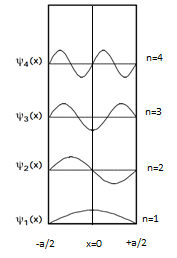
- Partícula en una caja con condición límite V (x) = 0 -a / 2 <x <+ a / 2
- En esta condición, la solución general será la misma, habrá un pequeño cambio en el resultado final, ya que las condiciones de contorno se cambian.
- En x = 0, la función de onda no es realmente cero en todo el valor de n.
- Claramente, del gráfico de variación de la función de onda que tenemos,
- En n = 1,3,4, ...... la función de onda sigue una curva de coseno con x = 0 como origen
- En n = 2,4,6, ...... la función de onda sigue una curva sinusoidal con x = 0 como origen
- A partir de esta observación, podemos concluir que la función de onda es alternativamente seno y coseno.
- Entonces, en este caso, la ecuación de onda resultante es
- ψ n (x) = Acos (k n x) n = 1,3,5, .............
- = Bsin (k n x) n = 2,4,6, .............
Potencial finito bien
Un pozo de potencial finito es la generalización del problema del pozo potencial infinito para pozos potenciales que tienen profundidad finita.
El problema del pozo potencial finito es matemáticamente más complicado que el problema infinito de partículas en una caja ya que la función de onda no está fijada a cero en las paredes del pozo. En cambio, la función de onda debe satisfacer condiciones de frontera matemática más complicadas ya que es distinta de cero en regiones fuera del pozo.
Barrera de potencial rectangular
Este es un modelo para el efecto de efecto túnel cuántico que desempeña un papel importante en el rendimiento de las tecnologías modernas, como la memoria flash y la microscopía de efecto túnel de barrido. La tunelización cuántica es fundamental para los fenómenos físicos implicados en superredes.
Oscilador armónico
Como en el caso clásico, el potencial para el oscilador armónico cuántico está dado por
Este problema puede tratarse resolviendo directamente la ecuación de Schrödinger, que no es trivial, o usando el "método de escalera" más elegante propuesto por primera vez por Paul Dirac. Los estados propios están dados por
donde H n son los polinomios de Hermite
y los niveles de energía correspondientes son
Este es otro ejemplo que ilustra la cuantificación de la energía para estados vinculados.
Potencial de paso
El potencial en este caso viene dado por:
Las soluciones son superposiciones de ondas en movimiento hacia la izquierda y hacia la derecha:
y
- ,
con los coeficientes A y B determinados a partir de las condiciones de contorno e imponiendo una derivada continua en la solución, y donde los vectores de onda están relacionados con la energía a través de
y
- .
Cada término de la solución se puede interpretar como un componente incidente, reflejado o transmitido de la onda, lo que permite el cálculo de los coeficientes de transmisión y reflexión. Notablemente, en contraste con la mecánica clásica, las partículas incidentes con energías mayores que el paso potencial se reflejan parcialmente.