Onda
Definición
En física, una onda es una perturbación que transfiere energía a través de la materia o el espacio, con poco o ningún transporte de masa asociado. Las ondas consisten en oscilaciones o vibraciones de un medio físico o un campo, alrededor de ubicaciones relativamente fijas.
Hay dos tipos principales de ondas: mecánica y electromagnética. Las ondas mecánicas se propagan a través de una materia física, cuya sustancia se está deformando. Las fuerzas de restauración invierten la deformación. Por ejemplo, las ondas de sonido se propagan a través de moléculas de aire colisionando con sus vecinos. Cuando las moléculas colisionan, también se alejan una de la otra (una fuerza restauradora). Esto evita que las moléculas continúen viajando en la dirección de la ola. Las ondas electromagnéticas no requieren un medio. En cambio, consisten en oscilaciones periódicas de campos eléctricos y magnéticos generados originalmente por partículas cargadas, y por lo tanto pueden viajar a través del vacío. Estos tipos varían en longitud de onda e incluyen ondas de radio, microondas, radiación infrarroja, luz visible, radiación ultravioleta, rayos X y rayos gamma.
Las olas se describen mediante una ecuación de onda que establece cómo se produce la perturbación a lo largo del tiempo. La forma matemática de esta ecuación varía según el tipo de onda. Además, el comportamiento de las partículas en la mecánica cuántica se describe mediante ondas. Además, las ondas gravitacionales también viajan a través del espacio, que son el resultado de una vibración o movimiento en los campos gravitacionales.
Una onda puede ser transversal, donde una perturbación crea oscilaciones que son perpendiculares a la propagación de la transferencia de energía, o longitudinal: las oscilaciones son paralelas a la dirección de propagación de la energía. Mientras que las ondas mecánicas pueden ser tanto transversales como longitudinales, todas las ondas electromagnéticas son transversales en el espacio libre.
Características generales
Una definición única y completa para el término onda no es sencilla. Una vibración se puede definir como un movimiento de ida y vuelta alrededor de un valor de referencia. Sin embargo, una vibración no es necesariamente una ola. Un intento de definir las características necesarias y suficientes que califican un fenómeno como una ola resulta en una línea borrosa.
El término onda A menudo se entiende intuitivamente que se refiere a un transporte de perturbaciones espaciales que generalmente no están acompañadas por un movimiento de un medio que ocupa este espacio como un todo. En una onda, la energía de una vibración se aleja de la fuente en forma de una perturbación dentro del medio circundante (Hall 1982, p.8). Sin embargo, este movimiento es problemático para una onda estacionaria (por ejemplo, una onda en una cuerda), donde la energía se mueve en ambas direcciones por igual, o para ondas electromagnéticas (por ejemplo, luz) en un vacío, donde el concepto de medio no aplicar y la interacción con un objetivo es la clave para la detección de olas y las aplicaciones prácticas. Hay olas de agua en la superficie del océano; ondas gamma y ondas de luz emitidas por el Sol; microondas utilizados en hornos de microondas y en equipos de radar; ondas de radio transmitidas por estaciones de radio;
Puede parecer que la descripción de las olas está estrechamente relacionada con su origen físico para cada instancia específica de un proceso de onda. Por ejemplo, la acústica se distingue de la óptica en que las ondas de sonido están relacionadas con una transferencia de onda mecánica en lugar de una onda electromagnética causada por la vibración. Conceptos tales como la masa, el momento, la inercia o la elasticidad se vuelven, por lo tanto, cruciales para describir los procesos de ondas acústicas (a diferencia de las ópticas). Esta diferencia de origen introduce ciertas características de onda particulares a las propiedades del medio involucrado. Por ejemplo, en el caso del aire: vórtices, presión de radiación, ondas de choque, etc .; en el caso de los sólidos: ondas de Rayleigh, dispersión; y así.
Sin embargo, otras propiedades, aunque generalmente se describen en términos de origen, pueden generalizarse a todas las ondas. Por tales razones, la teoría ondulatoria representa una rama particular de la física que se ocupa de las propiedades de los procesos de las ondas independientemente de su origen físico. Por ejemplo, en función del origen mecánico de las ondas acústicas, puede existir una perturbación en movimiento en el espacio-tiempo si y solo si el medio involucrado no es ni infinitamente rígido ni infinitamente flexible. Si todas las partes que componen un medio estuvieran rígidamente unidas, entonces todos vibrarían como uno solo, sin demora en la transmisión de la vibración y, por lo tanto, sin movimiento ondulatorio. Por otro lado, si todas las partes fueran independientes, entonces no habría transmisión de la vibración y tampoco movimiento de onda. Aunque las afirmaciones anteriores no tienen sentido en el caso de ondas que no requieren un medio, revelan una característica que es relevante para todas las ondas independientemente del origen: dentro de una onda, la fase de una vibración (es decir, su posición dentro de la vibración) ciclo) es diferente para los puntos adyacentes en el espacio porque la vibración alcanza estos puntos en diferentes momentos repetidamente.
Descripción matemática de ondas unidimensionales
Ecuación de onda
Considere una onda transversal móvil (que puede ser un pulso) en una cuerda (el medio). Considere que la cadena tiene una única dimensión espacial. Considera esta ola como viajar
- en la dirección en el espacio. Por ejemplo, deje que la dirección positiva sea hacia la derecha, y la dirección negativa hacia la izquierda.
- con amplitud constante
- con velocidad constante , donde está
- independiente de la longitud de onda (sin dispersión)
- independiente de la amplitud (medios lineales, no no lineales).
- con forma de onda constante o forma
Esta onda puede ser descrita por las funciones bidimensionales
- (forma de onda que viaja hacia la derecha)
- (forma de onda que viaja hacia la izquierda)
o, más generalmente, por la fórmula de d'Alembert:
representando dos formas de onda componentes y viajando a través del medio en direcciones opuestas. Una representación generalizada de esta onda se puede obtener como la ecuación diferencial parcial
Las soluciones generales se basan en el principio de Duhamel.
Formas de onda
La forma o forma de F en la fórmula de d'Alembert implica el argumento x - vt . Los valores constantes de este argumento corresponden a valores constantes de F, y estos valores constantes ocurren si x aumenta a la misma velocidad que vt . Es decir, la onda con forma de función F se moverá en la dirección x positiva a la velocidad v (y G se propagará a la misma velocidad en la dirección x negativa ).
En el caso de una función periódica F con período λ , es decir, F ( x + λ - vt ) = F ( x - vt ), la periodicidad de F en el espacio significa que una instantánea de la onda en un momento dado t encuentra la onda varía periódicamente en el espacio con el período λ (la longitud de onda de la onda). De manera similar, esta periodicidad de F también implica una periodicidad en el tiempo: F ( x - v (t + T) ) = F ( x - vt) siempre que vT = λ , por lo que una observación de la onda en una ubicación fija x encuentre la onda ondulando periódicamente en el tiempo con el período T = λ / v .
Amplitud y modulación
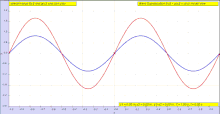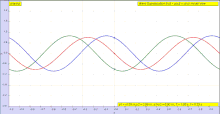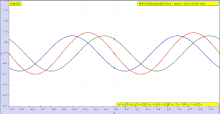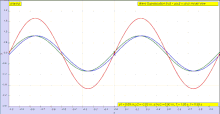
La amplitud de una onda puede ser constante (en cuyo caso la onda es una cw o de onda continua ), o puede ser modulada de manera que varíe con el tiempo y / o posición. El contorno de la variación en amplitud se llama envolvente de la onda. Matemáticamente, la onda modulada se puede escribir en la forma:
dónde está la envolvente de amplitud de la onda, es el número de onda y es la fase . Si la velocidad del grupo (ver abajo) es independiente de la longitud de onda, esta ecuación se puede simplificar como:
mostrando que la envolvente se mueve con la velocidad del grupo y conserva su forma. De lo contrario, en los casos en que la velocidad del grupo varía con la longitud de onda, la forma del pulso cambia de una manera a menudo descrita usando una ecuación de envolvente .
Velocidad de fase y velocidad de grupo
Hay dos velocidades que están asociadas con las ondas, la velocidad de fase y la velocidad del grupo.
La velocidad de fase es la velocidad a la que la fase de la onda se propaga en el espacio: cualquier fase dada de la onda (por ejemplo, la cresta) parecerá viajar a la velocidad de fase. La velocidad de fase se da en términos de la longitud de onda λ (lambda) y el período T como
La velocidad de grupo es una propiedad de las ondas que tienen una envolvente definida, que mide la propagación a través del espacio (es decir, la velocidad de fase) de la forma general de las amplitudes de las ondas: modulación o envolvente de la onda.
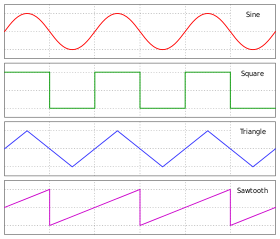
Ondas sinusoidales
Matemáticamente, la onda más básica es la onda sinusoidal(espacialmente) unidimensional (o onda armónica o sinusoide ) con una amplitud descrita por la ecuación:
dónde
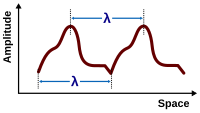
- es la amplitud máxima de la onda, la distancia máxima desde el punto más alto de la perturbación en el medio (la cresta) hasta el punto de equilibrio durante un ciclo de onda. En la ilustración de la derecha, esta es la distancia vertical máxima entre la línea de base y la onda.
- es el espacio coordinado
- es la coordenada del tiempo
- es el número de onda
- es la frecuencia angular
- es la fase constante.
Las unidades de la amplitud dependen del tipo de onda. Las ondas mecánicas transversales (p. Ej., Una onda en una cuerda) tienen una amplitud expresada como distancia (p. Ej., Metros), ondas mecánicas longitudinales (p. Ej., Ondas de sonido) utilizan unidades de presión (por ejemplo, pascales) y ondas electromagnéticas (una forma de onda de vacío transversal) expresa la amplitud en términos de su campo eléctrico (por ejemplo, voltios / metro).
La longitud de onda es la distancia entre dos crestas o valles secuenciales (u otros puntos equivalentes), generalmente se mide en metros. Un número de onda , la frecuencia espacial de la onda en radianes por unidad de distancia (típicamente por metro), puede asociarse con la longitud de onda por la relación
El período es el tiempo para un ciclo completo de una oscilación de una onda. La frecuencia es el número de períodos por unidad de tiempo (por segundo) y se mide típicamente en hertz denotado como Hz. Estos están relacionados por:
En otras palabras, la frecuencia y el período de una onda son recíprocos.
La frecuencia angular representa la frecuencia en radianes por segundo. Está relacionado con la frecuencia o el período por
La longitud de onda de una onda sinusoidal que viaja a velocidad constante viene dada por:
donde se llama velocidad de fase (magnitud de la velocidad de fase) de la onda y es la frecuencia de la onda.
La longitud de onda puede ser un concepto útil incluso si la onda no es periódica en el espacio. Por ejemplo, en una ola oceánica que se acerca a la costa, la onda entrante se ondula con una longitud de onda local variable que depende en parte de la profundidad del fondo marino en comparación con la altura de la ola. El análisis de la ola puede basarse en la comparación de la longitud de onda local con la profundidad del agua local.
Aunque las formas de onda arbitrarias se propagarán sin cambios en los sistemas invariantes de tiempo lineales sin pérdidas, en presencia de dispersión la onda sinusoidal es la única forma que se propagará sin cambios, excepto por la fase y la amplitud, lo que facilita el análisis. Debido a las relaciones Kramers-Kronig, un medio lineal con dispersión también presenta pérdida, por lo que la onda sinusoidal que se propaga en un medio dispersivo se atenúa en ciertos rangos de frecuencia que dependen del medio. La función seno es periódica, por lo que la onda senoidal o sinusoidal tiene una longitud de onda en el espacio y un período de tiempo.
La sinusoide se define para todos los tiempos y distancias, mientras que en situaciones físicas generalmente tratamos con ondas que existen para un lapso de tiempo limitado en el espacio y la duración. Afortunadamente, una forma de onda arbitraria se puede descomponer en un conjunto infinito de ondas sinusoidales mediante el uso del análisis de Fourier. Como resultado, el caso simple de una sola onda sinusoidal se puede aplicar a casos más generales. En particular, muchos medios son lineales, o casi, de modo que el cálculo del comportamiento de onda arbitrario se puede encontrar sumando respuestas a ondas sinusoidales individuales utilizando el principio de superposición para encontrar la solución para una forma de onda general. Cuando un medio no es lineal, la respuesta a ondas complejas no puede determinarse a partir de una descomposición de onda sinusoidal.
Ondas planas
Ondas estacionarias
Una onda estacionaria, también conocida como onda estacionaria , es una onda que permanece en una posición constante. Este fenómeno puede ocurrir porque el medio se mueve en la dirección opuesta a la onda, o puede surgir en un medio estacionario como resultado de la interferencia entre dos ondas que viajan en direcciones opuestas.
La suma de dos ondas contrapropagantes (de igual amplitud y frecuencia) crea una onda estacionaria . Las ondas estacionarias surgen comúnmente cuando un límite bloquea la propagación adicional de la onda, lo que provoca la reflexión de la onda y, por lo tanto, la introducción de una onda que se propaga en sentido contrario. Por ejemplo, cuando se desplaza una cuerda de violín, las ondas transversales se propagan hacia donde la cuerda se mantiene en su lugar en el puente y la tuerca, donde las ondas se reflejan hacia atrás. En el puente y la tuerca, las dos ondas opuestas están en antifase y se cancelan mutuamente, produciendo un nodo. A medio camino entre dos nodos hay un antinodo, donde las dos ondas que se propagan en sentido contrario se potencian mutuamente. No hay propagación neta de energía en el tiempo.
 Ondas estables unidimensionales; el modo fundamental y los primeros 5 armónicos.
Ondas estables unidimensionales; el modo fundamental y los primeros 5 armónicos. Una onda estacionaria bidimensional en un disco; este es el modo fundamental.
Una onda estacionaria bidimensional en un disco; este es el modo fundamental. Una onda estacionaria en un disco con dos líneas nodales cruzadas en el centro; esto es un sobretono.
Una onda estacionaria en un disco con dos líneas nodales cruzadas en el centro; esto es un sobretono.
Propiedades físicas
Las ondas exhiben comportamientos comunes bajo una serie de situaciones estándar, por ejemplo
Transmisión y medios
Las ondas normalmente se mueven en línea recta (es decir, rectilíneamente) a través de un medio de transmisión . Dichos medios se pueden clasificar en una o más de las siguientes categorías:
- Un medio delimitado si es de extensión finita, de lo contrario un medio sin límites
- Un medio lineal si se pueden agregar las amplitudes de diferentes ondas en cualquier punto particular del medio
- Un medio uniforme u homogéneo si sus propiedades físicas no se modifican en diferentes lugares del espacio
- Un medio anisotrópico si una o más de sus propiedades físicas difieren en una o más direcciones
- Un medio isotrópico si sus propiedades físicas son las mismas en todas las direcciones
Absorción
La absorción de las olas significa que si un tipo de onda golpea una materia, será absorbida por la materia. Cuando una onda con esa misma frecuencia natural incide sobre un átomo, entonces los electrones de ese átomo se pondrán en movimiento vibratorio. Si una onda de una frecuencia dada choca contra un material con electrones que tienen las mismas frecuencias vibratorias, entonces esos electrones absorberán la energía de la onda y la transformarán en movimiento vibratorio.
Reflexión
Cuando una onda golpea una superficie reflectante, cambia de dirección, de modo que el ángulo formado por la onda incidente y la línea normal a la superficie es igual al ángulo formado por la onda reflejada y la misma línea normal.
Refracción
La refracción es el fenómeno de una ola que cambia su velocidad. Matemáticamente, esto significa que el tamaño de la velocidad de fase cambia. Típicamente, la refracción ocurre cuando una onda pasa de un medio a otro. La cantidad por la cual una onda es refractada por un material viene dada por el índice de refracción del material. Las direcciones de incidencia y refracción están relacionadas con los índices de refracción de los dos materiales según la ley de Snell.
Difracción
Una onda presenta difracción cuando encuentra un obstáculo que dobla la onda o cuando se extiende después de emerger de una abertura. Los efectos de difracción son más pronunciados cuando el tamaño del obstáculo o abertura es comparable a la longitud de onda de la onda.
Interferencia
Las ondas que se encuentran se combinan a través de la superposición para crear una nueva onda llamada patrón de interferencia. Se producen patrones de interferencia importantes para las ondas que están en fase.
Polarización
El fenómeno de la polarización surge cuando el movimiento de la onda puede ocurrir simultáneamente en dos direcciones ortogonales. Las ondas transversales pueden estar polarizadas, por ejemplo. Cuando la polarización se usa como un descriptor sin calificación, generalmente se refiere al caso especial y simple de polarización lineal. Una onda transversal está polarizada linealmente si oscila en una sola dirección o plano. En el caso de la polarización lineal, a menudo es útil agregar la orientación relativa de ese plano, perpendicular a la dirección de desplazamiento, en la que se produce la oscilación, como "horizontal", por ejemplo, si el plano de polarización es paralelo al suelo. Las ondas electromagnéticas que se propagan en el espacio libre, por ejemplo, son transversales; pueden polarizarse mediante el uso de un filtro polarizador.
Las ondas longitudinales, como las ondas de sonido, no presentan polarización. Para estas ondas solo hay una dirección de oscilación, es decir, a lo largo de la dirección de desplazamiento.
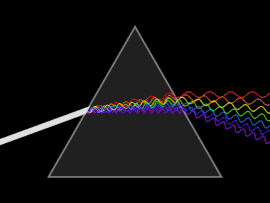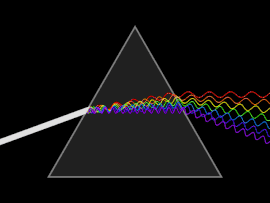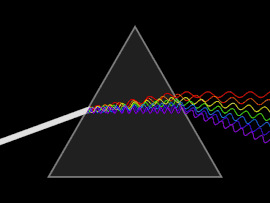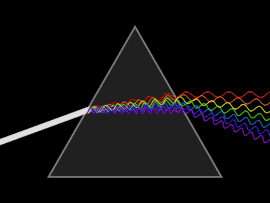
Dispersión
Una onda experimenta dispersión cuando la velocidad de fase o la velocidad de grupo depende de la frecuencia de onda. La dispersión se ve más fácilmente al dejar pasar la luz blanca a través de un prisma, cuyo resultado es producir el espectro de colores del arco iris. Isaac Newton realizó experimentos con luz y prismas, presentando sus hallazgos en Opticks (1704) que la luz blanca consiste en varios colores y que estos colores no se pueden descomponer más.
Ondas mecánicas
Waves en cuerdas
La velocidad de una onda transversal que viaja a lo largo de una cuerda vibratoria ( v ) es directamente proporcional a la raíz cuadrada de la tensión de la cuerda ( T ) sobre la densidad de masa lineal ( μ ):
donde la densidad lineal μ es la masa por unidad de longitud de la cuerda.
Ondas acústicas
Las ondas acústicas o de sonido viajan a la velocidad dada por
o la raíz cuadrada del módulo adiabático a granel dividido por la densidad del fluido ambiental (ver velocidad del sonido).
Olas de agua
- Las ondas en la superficie de un estanque son en realidad una combinación de ondas transversales y longitudinales; por lo tanto, los puntos en la superficie siguen caminos orbitales.
- Sonido: una onda mecánica que se propaga a través de gases, líquidos, sólidos y plasmas;
- Ondas inerciales, que ocurren en fluidos rotatorios y son restauradas por el efecto Coriolis;
- Ondas de superficie oceánica, que son perturbaciones que se propagan a través del agua.
Ondas sísmicas
Las ondas sísmicas son ondas de energía que viajan a través de las capas de la Tierra y son el resultado de terremotos, erupciones volcánicas, movimientos de magma, grandes derrumbes y grandes explosiones hechas por el hombre que producen energía acústica de baja frecuencia.
Ondas de choque

Una onda de choque es un tipo de perturbación que se propaga. Cuando una onda se mueve más rápido que la velocidad local del sonido en un fluido, es una onda de choque. Al igual que una onda ordinaria, una onda de choque transporta energía y puede propagarse a través de un medio; sin embargo, se caracteriza por un cambio abrupto, casi discontinuo en la presión, temperatura y densidad del medio.
Otro
- Ondas de tráfico, es decir, propagación de diferentes densidades de vehículos de motor, etc., que pueden modelarse como ondas cinemáticas
- La onda metacrónica se refiere a la aparición de una onda viajera producida por acciones secuenciales coordinadas.
Ondas electromagnéticas
Una onda electromagnética consiste en dos ondas que son oscilaciones de los campos eléctricos y magnéticos. Una onda electromagnética viaja en una dirección que está en ángulo recto con la dirección de oscilación de ambos campos. En el siglo XIX, James Clerk Maxwell demostró que, en el vacío, los campos eléctricos y magnéticos satisfacen la ecuación de onda con una velocidad igual a la de la velocidad de la luz. De esto surgió la idea de que la luz es una onda electromagnética. Las ondas electromagnéticas pueden tener diferentes frecuencias (y por lo tanto longitudes de onda), dando lugar a diversos tipos de radiación, como ondas de radio, microondas, infrarrojos, luz visible, ultravioleta, rayos X y rayos gamma.
Ondas mecánicas cuánticas
Ecuación de Schrödinger
La ecuación de Schrödinger describe el comportamiento ondulatorio de las partículas en la mecánica cuántica. Las soluciones de esta ecuación son funciones de onda que pueden usarse para describir la densidad de probabilidad de una partícula.
Ecuación de Dirac
La ecuación de Dirac es una ecuación de onda relativista que detalla las interacciones electromagnéticas. Las ondas de Dirac explicaron los detalles finos del espectro de hidrógeno de una manera completamente rigurosa. La ecuación de onda también implicaba la existencia de una nueva forma de materia, antimateria, previamente insospechada e inobservada y que fue confirmada experimentalmente. En el contexto de la teoría de campos cuánticos, la ecuación de Dirac se reinterpreta para describir campos cuánticos correspondientes a spin-½ partículas.
de Broglie olas
Louis de Broglie postuló que todas las partículas con impulso tienen una longitud de onda
donde h es la constante de Planck, y p es la magnitud del momento de la partícula. Esta hipótesis fue la base de la mecánica cuántica. Hoy en día, esta longitud de onda se denomina longitud de onda de Broglie. Por ejemplo, los electrones en una pantalla CRT tienen una longitud de onda de De Broglie de aproximadamente 10 m.
Una onda que representa una partícula de este tipo que viaja en la dirección k se expresa mediante la función de onda de la siguiente manera:
donde la longitud de onda está determinada por el vector de onda k como:
y el impulso por:
Sin embargo, una onda como esta con una longitud de onda definida no se localiza en el espacio, y por lo tanto no puede representar una partícula localizada en el espacio. Para localizar una partícula, de Broglie propuso una superposición de diferentes longitudes de onda que se extienden alrededor de un valor central en un paquete de ondas, una forma de onda utilizada a menudo en mecánica cuántica para describir la función de onda de una partícula. En un paquete de ondas, la longitud de onda de la partícula no es precisa, y la longitud de onda local se desvía en cualquier lado del valor de la longitud de onda principal.
Al representar la función de onda de una partícula localizada, a menudo se toma el paquete de onda para que tenga una forma gaussiana y se denomina paquete de onda gaussiano . Los paquetes de ondas gaussianas también se utilizan para analizar las ondas de agua.
Por ejemplo, una función de onda gaussiana ψ podría tomar la forma:
en algún momento inicial t = 0, donde la longitud de onda central está relacionada con el vector de onda central k 0 como λ 0 = 2π / k 0 . Es bien sabido de la teoría del análisis de Fourier, o del principio de incertidumbre de Heisenberg (en el caso de la mecánica cuántica) que se necesita un rango estrecho de longitudes de onda para producir un paquete de onda localizado, y cuanto más localizada es la envolvente, mayor se extendió en las longitudes de onda requeridas. La transformada de Fourier de un gaussiano es en sí misma gaussiana. Dado el Gaussian:
la transformada de Fourier es:
El gaussiano en el espacio por lo tanto está compuesto de ondas:
es decir, un número de ondas de longitudes de onda λ tales que k λ = 2 π.
El parámetro σ decide la dispersión espacial del gaussiano a lo largo del eje x , mientras que la transformada de Fourier muestra un margen en el vector de onda k determinado por 1 / σ. Es decir, cuanto menor es la extensión en el espacio, mayor es la extensión en ky , por lo tanto, en λ = 2π / k .
Ondas de gravedad
Las ondas de gravedad son ondas generadas en un medio fluido o en la interfaz entre dos medios cuando la fuerza de la gravedad o flotabilidad intenta restaurar el equilibrio. Una onda en un estanque es un ejemplo.
Ondas gravitacionales
Las ondas gravitacionales también viajan a través del espacio. La primera observación de ondas gravitacionales se anunció el 11 de febrero de 2016. Las ondas gravitacionales son perturbaciones en la curvatura del espacio-tiempo, predichas por la teoría de la relatividad general de Einstein.