0 (constantes matemáticas)
Definición
| ||||
|---|---|---|---|---|
-1 0 1 2 3 4 5 6 7 8 9 → Lista de números: enteros ← 0 10 20 30 40 50 60 70 80 90 → | ||||
| Cardenal | 0, cero, "oh" ( / oʊ / ) , nada, nada, nada | |||
| Ordinal | Zeroth, casi | |||
| Divisores | Todos los números | |||
| Binario | 0 2 | |||
| Ternario | 0 3 | |||
| Cuaternario | 0 4 | |||
| Quinario | 0 5 | |||
| Senario | 0 6 | |||
| Octal | 0 8 | |||
| Duodecimal | 0 12 | |||
| Hexadecimal | 0 16 | |||
| Vigesimal | 0 20 | |||
| Base 36 | 0 36 | |||
| Árabe y kurdo | 0 | |||
| Urdu | ||||
| bengalí | 0 | |||
| Números hindúes | 0 | |||
| chino | 零, 〇 | |||
| japonés | 零, 〇 | |||
| Khmer | 0 | |||
| tailandés | 0 | |||
Etimología
La palabra cero entró en el idioma inglés a través del zéro francés del cero italiano, contracción italiana de la forma zevero veneciana de ' zefiro italiano mediante ṣafira o ṣifr . En el tiempo preislámico, la palabra ṣifr (árabe صفر) tenía el significado "vacío". Sifr evolucionó para significar cero cuando se usó para traducir śūnya (sánscrito: शून्य) de la India. El primer uso conocido de cero en inglés fue en 1598.
The Italian mathematician Fibonacci (c. 1170–1250), who grew up in North Africa and is credited with introducing the decimal system to Europe, used the term zephyrum. This became zefiroin Italian, and was then contracted to zero in Venetian. The Italian word zefiro was already in existence (meaning "west wind" from Latin and Greek zephyrus) and may have influenced the spelling when transcribing Arabic ṣifr.
Modern usage
Hay diferentes palabras usadas para el número o concepto de cero dependiendo del contexto. Para la simple noción de falta, las palabras nada y ninguna se usan a menudo. A veces las palabras nada , nada y nada se usan. Varios deportes tienen palabras específicas para cero, como nulo en el fútbol de asociación (fútbol), el amor en el tenis y un pato en el cricket. A menudo se llama oh en el contexto de los números de teléfono. Las palabras de la jerga cero incluyen zip , zilch , naday scratch. Huevo de pato y el huevo de ganso también es jerga para cero.
Historia
Antiguo Cercano Oriente
| nfr | corazón con tráquea hermosa, agradable, buena |
|---|
A mediados del segundo milenio antes de Cristo, las matemáticas babilónicas tenían un sofisticado sistema de numeración posicional sexagesimal. La falta de un valor posicional (o cero) se indicó por un espacio entre los números sexagesimales. Para el año 300 a. C., un símbolo de puntuación (dos cuñas inclinadas) se cooptó como marcador de posición en el mismo sistema babilónico. En una tableta desenterrada en Kish (que data de alrededor del 700 aC), el escriba Bêl-bân-aplu escribió sus ceros con tres ganchos, en lugar de dos cuñas inclinadas.
El marcador de posición babilónico no era un cero verdadero porque no se usó solo. Tampoco se usó al final de un número. Por lo tanto, números como 2 y 120 (2 × 60), 3 y 180 (3 × 60), 4 y 240 (4 × 60), parecían iguales porque los números más grandes carecían de un marcador de posición final sexagesimal. Solo el contexto podría diferenciarlos.
América precolombina
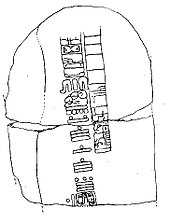
El calendario mesoamericano de la cuenta larga desarrollado en el centro-sur de México y América Central requirió el uso de cero como marcador de posición dentro de su sistema de numeración posicional vigesimal (base-20). Muchos glifos diferentes, incluido este cuatrifolio parcial, se  usaron como un símbolo cero para estas fechas de Cuenta larga, la primera de las cuales (en la estela 2 en Chiapa de Corzo, Chiapas) tiene una fecha de 36 a.
usaron como un símbolo cero para estas fechas de Cuenta larga, la primera de las cuales (en la estela 2 en Chiapa de Corzo, Chiapas) tiene una fecha de 36 a.
Dado que las primeras ocho fechas de la Cuenta Larga aparecen fuera de la tierra natal Maya, generalmente se cree que el uso del cero en las Américas es anterior a los Mayas y posiblemente fue la invención de los Olmecas. Muchas de las primeras fechas de la Cuenta Larga se encontraron dentro del corazón de los olmecas, aunque la civilización olmeca terminó en el siglo IV aC , varios siglos antes de las fechas más antiguas conocidas de la Cuenta Larga.
Aunque el cero se convirtió en una parte integral de los números mayas, con una "forma de concha" similar a una tortuga vacía diferente utilizada para muchas representaciones del número "cero", se supone que no ha influido en los sistemas de numeración del Viejo Mundo.
Quipu, un dispositivo de cordón anudado, utilizado en el Imperio Inca y sus sociedades predecesoras en la región andina para registrar datos contables y otros datos digitales, está codificado en un sistema de posición de base diez. Cero está representado por la ausencia de un nudo en la posición adecuada.
Antigüedad clásica
Los antiguos griegos no tenían ningún símbolo para cero (μηδέν), y no usaban un marcador de posición de dígitos para ello. Parecían inseguros sobre el estado de cero como número. Se preguntaban a sí mismos: "¿Cómo puede nada ser algo?", Lo que lleva a argumentos filosóficos y, en la época medieval, religiosos sobre la naturaleza y la existencia del cero y el vacío. Las paradojas de Zeno de Elea dependen en gran parte de la interpretación incierta del cero.
Hacia el 130 dC, Ptolomeo, influenciado por Hiparco y los babilonios, estaba usando un símbolo de cero (un pequeño círculo con una barra de arriba) en su trabajo sobre astronomía matemática llamado Syntaxis Mathematica , también conocido como el Almagesto.. La forma en que se usa se puede ver en su tabla de acordes en ese libro. El cero de Ptolomeo se usó dentro de un sistema de numeración sexagesimal, de lo contrario se usarían numerales griegos alfabéticos. Debido a que se usó solo, no solo como marcador de posición, este cero helenístico fue quizás el uso más antiguo documentado de un número que representa cero en el Viejo Mundo. Sin embargo, las posiciones generalmente se limitaban a la parte fraccional de un número (llamadas minutos, segundos, tercios, cuartos, etc.) - no se usaban para la parte integral de un número, lo que indica un concepto quizás mejor expresado como "ninguno" , en lugar de "cero" en el sentido moderno. En los manuscritos bizantinos posteriores del Almagesto de Ptolomeo , el cero helenístico se había transformado en la letra griega omicron (que significa 70).
Otro cero se utilizó en las tablas junto con los números romanos en 525 (primer uso conocido por Dionysius Exiguus), pero como una palabra, nulla que significa "nada", no como un símbolo. Cuando la división produjo cero como residuo , se usó nihil , que también significa "nada". Estos ceros medievales fueron utilizados por todas las futuras calculadoras medievales de Pascua. La inicial "N" fue usada como un símbolo cero en una tabla de números romanos por Bede o sus colegas alrededor del 725.
China
El Sūnzĭ Suànjīng , de fecha desconocida, pero se estima que data del siglo I al V dC , y los registros japoneses datan del siglo XVIII, describen cómo el c. El sistema de conteo de barras chino del siglo IV aC permite realizar cálculos decimales. Según A History of Mathematics , las varillas "dieron la representación decimal de un número, con un espacio vacío que denota cero". El sistema de varillas de conteo se considera un sistema de notación posicional.
En el año 690 DC, la Emperatriz Wǔ promulgó caracteres zetianos, uno de los cuales era "〇". La palabra ahora se usa como sinónimo del número cero.
Zero no fue tratado como un número en ese momento, sino como un "puesto vacante". El Tratado matemático 1247 de Qín Jiǔsháo en Nueve Secciones es el texto matemático chino más antiguo que sobrevive usando un símbolo redondo para cero. Los autores chinos habían estado familiarizados con la idea de los números negativos de la dinastía Han (siglo II dC) , como se ve en Los Nueve Capítulos sobre el Arte Matemático , mucho antes del siglo XV cuando se establecieron bien en Europa.
India
Pingala (hacia el 3º / 2º siglo aC), un erudito de prosodias sánscritas, usó números binarios en forma de sílabas cortas y largas (la última igual a dos sílabas cortas), una notación similar al código Morse. Pingala usó la palabra sánscrita śūnya explícitamente para referirse a cero.
Se consideró que el texto más antiguo para usar un sistema de valor de lugar decimal, incluyendo un cero, es el Lokavibhāga , un texto jainista sobre cosmología que sobrevive en una traducción sánscrita medieval del original de Prakrit, que data internamente del año 458 d. C. (Era de Saka 380). En este texto, śūnya ("vacío, vacío") también se usa para referirse a cero.
En todo el manuscrito de Bakhshali, un manual práctico sobre aritmética para comerciantes, cuya fecha era incierta, se utiliza un símbolo para cero, un gran punto que probablemente sea el precursor del símbolo hueco todavía en uso. En 2017, tres muestras del manuscrito se muestran por datación por radiocarbono que provienen de tres siglos diferentes: desde 224 hasta 383 dC, 680-779 dC y 885-993 dC, por lo que es el uso registrado más antiguo del símbolo cero en el mundo. No se sabe cómo los fragmentos de corteza de abedul de diferentes siglos que forman el manuscrito llegaron a ser empaquetados juntos.
El origen de la notación de valor de lugar basada en el decimal moderno se puede remontar a Aryabhatiya ( c.500 ), que establece sthānāt sthānaṁ daśaguṇaṁ syāt "de lugar en lugar, cada uno es diez veces el precedente". El concepto de cero como un dígito en la notación del valor del lugar decimal se desarrolló en la India, presumiblemente ya en el período Gupta (hacia el siglo V) , con la evidencia inequívoca más antigua que data del siglo VII.
Las reglas que rigen el uso del cero aparecieron por primera vez en Brahmagupta's Brahmasputha Siddhanta (siglo VII). Este trabajo considera no solo cero, sino números negativos, y las reglas algebraicas para las operaciones elementales de la aritmética con tales números. En algunos casos, sus reglas difieren del estándar moderno, específicamente la definición del valor de cero dividido por cero como cero.
Epigrafía
Hay numerosas inscripciones de placas de cobre, con el mismo pequeño o en ellas, algunas de ellas datadas posiblemente en el siglo VI, pero su fecha o autenticidad pueden estar en duda.
Una tableta de piedra encontrada en las ruinas de un templo cerca de Sambor en el Mekong, provincia de Kratié, Camboya, incluye la inscripción "605" en números jemeres (un conjunto de glifos numerales de la familia de los números hindúes). El número es el año de la inscripción en la era Saka, que corresponde a una fecha del año 683 DC.
El primer uso conocido de glifos especiales para los dígitos decimales que incluye la apariencia indudable de un símbolo para el dígito cero, un círculo pequeño, aparece en una inscripción de piedra hallada en el templo de Chaturbhuja en Gwalior, India, con fecha 876. También se usa cero. como marcador de posición en el manuscrito de Bakhshali, partes de las cuales datan de AD 224-383.
Edades medias
Transmisión a la cultura islámica
La herencia de la ciencia en lengua árabe fue en gran parte griega, seguida de influencias hindúes. En 773, a instancias de Al-Mansur, se hicieron traducciones de muchos tratados antiguos, incluidos griego, romano, indio y otros.
En el año 813, las tablas astronómicas fueron preparadas por un matemático persa, Muḥammad ibn Mūsā al-Khwārizmī, utilizando numerales hindúes; y alrededor de 825, publicó un libro que sintetiza el conocimiento griego e hindú y también contenía su propia contribución a las matemáticas, incluida una explicación del uso de cero. Este libro fue traducido al latín en el siglo XII bajo el título Algoritmi de numero Indorum . Este título significa "al-Khwarizmi en los Números de los Indios". La palabra "Algoritmi" era la latinización del traductor del nombre de Al-Khwarizmi, y la palabra "Algoritmo" o "Algorismo" comenzó a significar cualquier aritmética basada en decimales.
Muhammad ibn Ahmad al-Khwarizmi, en 976, declaró que si no aparece un número en lugar de decenas en un cálculo, se debe usar un pequeño círculo "para mantener las filas". Este círculo se llamaba ṣifr .
Transmisión a Europa
El sistema numérico hindú-árabe (base 10) llegó a Europa en el siglo XI, a través de la Península Ibérica a través de los musulmanes españoles, los moros, junto con el conocimiento de la astronomía y los instrumentos como el astrolabio, primero importado por Gerberto de Aurillac. Por esta razón, los números llegaron a ser conocidos en Europa como "números arábigos". El matemático italiano Fibonacci o Leonardo de Pisa fue instrumental en llevar el sistema a las matemáticas europeas en 1202, declarando:
Aquí, Leonardo de Pisa usa la frase "signo 0", que indica que es como un signo para realizar operaciones como la suma o la multiplicación. Desde el siglo XIII, los manuales de cálculo (suma, multiplicación, extracción de raíces, etc.) se volvieron comunes en Europa, donde se denominaron algorismus en honor al matemático persa al-Khwārizmī. El más popular fue escrito por Johannes de Sacrobosco, alrededor de 1235 y fue uno de los primeros libros científicos que se imprimirá en 1488. Hasta finales del siglo XV, los números hindúes-arábigos parecen haber predominado entre los matemáticos, mientras que los comerciantes prefirieron usar el romano numerales En el siglo XVI, llegaron a ser de uso común en Europa.
Matemáticas
0 es el entero inmediatamente anterior a 1. Cero es un número par porque es divisible por 2 sin resto. 0 no es ni positivo ni negativo. Según la mayoría de las definiciones, 0 es un número natural, y luego el único número natural que no es positivo. Cero es un número que cuantifica un recuento o una cantidad de tamaño nulo. En la mayoría de las culturas, 0 se identificó antes de que se aceptara la idea de cosas negativas o cantidades menores que cero.
El valor, o número , cero no es lo mismo que el dígito cero, que se usa en sistemas numéricos que usan notación posicional. Las posiciones sucesivas de los dígitos tienen pesos más altos, por lo que dentro de un número el dígito cero se usa para omitir una posición y dar los pesos adecuados a los dígitos anteriores y siguientes. Un dígito cero no siempre es necesario en un sistema numérico posicional, por ejemplo, en el número 02. En algunos casos, se puede usar un cero inicial para distinguir un número.
Álgebra elemental
El número 0 es el número entero no negativo más pequeño. El número natural después de 0 es 1 y ningún número natural precede 0. El número 0 puede o no considerarse un número natural, pero es un número entero y, por lo tanto, un número racional y un número real (así como un número algebraico y un número complejo).
El número 0 no es positivo ni negativo y generalmente se muestra como el número central en una recta numérica. No es ni un número primo ni un número compuesto. No puede ser primo porque tiene un número infinito de factores, y no puede ser compuesto porque no puede expresarse como un producto de números primos (0 siempre debe ser uno de los factores). Zero es, sin embargo, incluso (además de ser un múltiplo de cualquier otro número entero, racional o real).
Las siguientes son algunas reglas básicas (elementales) para tratar con el número 0. Estas reglas se aplican a cualquier número real o complejo x , a menos que se indique lo contrario.
- Adición: x + 0 = 0 + x = x . Es decir, 0 es un elemento de identidad (o elemento neutral) con respecto a la suma.
- Resta: x - 0 = x y 0 - x = - x .
- Multiplicación: x • 0 = 0 • x = 0.
- División: 0x = 0, para distinto de cero x . Pero x0 no está definido, porque 0 no tiene inversión multiplicativa (ningún número real multiplicado por 0 produce 1), una consecuencia de la regla anterior.
- Exponenciación: x = xx = 1, excepto que el caso x = 0 puede quedar indefinido en algunos contextos. Para todo positivo real x , 0 = 0 .
La expresión 00 , que se puede obtener en un intento de determinar el límite de una expresión de la forma f ( x )g ( x ) como resultado de aplicar el operador lim independientemente para los dos operandos de la fracción, es una la llamada "forma indeterminada". Eso no significa simplemente que el límite buscado sea necesariamente indefinido; más bien, significa que el límite de f ( x )g ( x ) , si existe, debe encontrarse por otro método, como la regla de l'Hôpital.
La suma de 0 números (la suma vacía ) es 0, y el producto de 0 números (el producto vacío ) es 1. ¡El factorial 0! evalúa a 1, como un caso especial del producto vacío.
Otras ramas de las matemáticas
- En la teoría de conjuntos, 0 es la cardinalidad del conjunto vacío: si uno no tiene manzanas, entonces uno tiene 0 manzanas. De hecho, en ciertos desarrollos axiomáticos de las matemáticas a partir de la teoría de conjuntos, 0 se define como el conjunto vacío. Cuando se hace esto, el conjunto vacío es la asignación cardinal de Von Neumann para un conjunto sin elementos, que es el conjunto vacío. La función de cardinalidad, aplicada al conjunto vacío, devuelve el conjunto vacío como un valor, asignándole de ese modo 0 elementos.
- También en la teoría de conjuntos, 0 es el número ordinal más bajo, que corresponde al conjunto vacío visto como un conjunto bien ordenado.
- En la lógica proposicional, 0 puede usarse para denotar el valor de verdad como falso.
- En álgebra abstracta, 0 se usa comúnmente para denotar un elemento cero, que es un elemento neutral para la suma (si se define en la estructura considerada) y un elemento absorbente para la multiplicación (si está definido).
- En la teoría de celosía, 0 puede denotar el elemento inferior de un enrejado delimitado.
- En la teoría de categorías, 0 a veces se usa para denotar un objeto inicial de una categoría.
- En la teoría de la recursión, 0 puede usarse para denotar el grado de Turing de las funciones computables parciales.
Términos matemáticos relacionados
- Un cero de una función f es un punto x en el dominio de la función tal que f ( x ) = 0 . Cuando hay un número finito de ceros, se llaman raíces de la función. Esto está relacionado con ceros de una función holomórfica.
- La función de cero (o mapa cero) en un dominio D es la función constante con 0 como su único valor de salida posible, es decir, la función f definida por f ( x ) = 0 para todas las x en D . La función cero es la única función que es par e impar. Una función cero particular es un morfismo cero en la teoría de categorías; por ejemplo, un mapa cero es la identidad en el grupo aditivo de funciones. El determinante en matrices cuadradas no invertibles es un mapa cero.
- Varias ramas de las matemáticas tienen cero elementos, que generalizan la propiedad 0 + x = x , o la propiedad 0 • x = 0, o ambas.
Física
El valor cero juega un papel especial para muchas cantidades físicas. Para algunas cantidades, el nivel cero se distingue naturalmente de todos los otros niveles, mientras que para otros se elige de forma más o menos arbitraria. Por ejemplo, para una temperatura absoluta (medida en kelvins), cero es el valor más bajo posible (las temperaturas negativas están definidas, pero los sistemas de temperatura negativa en realidad no son más fríos). Esto está en contraste con, por ejemplo, las temperaturas en la escala Celsius, donde el cero se define arbitrariamente para estar en el punto de congelación del agua. Al medir la intensidad del sonido en decibelios o infones, el nivel cero se establece arbitrariamente en un valor de referencia, por ejemplo, en un valor para el umbral de audición. En física,
Química
Zero ha sido propuesto como el número atómico del elemento teórico tetraneutron. Se ha demostrado que un grupo de cuatro neutrones puede ser lo suficientemente estable como para ser considerado un átomo por derecho propio. Esto crearía un elemento sin protones y sin carga en su núcleo.
Ya en 1926, Andreas von Antropoff acuñó el término neutronio para una forma conjeturada de materia compuesta de neutrones sin protones, que colocó como el elemento químico del número atómico cero en la cabecera de su nueva versión de la tabla periódica. Posteriormente se colocó como un gas noble en el medio de varias representaciones espirales del sistema periódico para clasificar los elementos químicos.
Ciencias de la Computación
La práctica más común en toda la historia de la humanidad ha sido comenzar a contar en uno, y esta es la práctica en los primeros lenguajes de programación de ciencias de la computación clásica como Fortran y COBOL. Sin embargo, a fines de la década de 1950 LISP introdujo numeración basada en cero para matrices, mientras que Algol 58 introdujo bases completamente flexibles para subíndices de matriz (permitiendo cualquier entero positivo, negativo o cero como base para subíndices de matriz), y la mayoría de los lenguajes de programación subsiguientes adoptaron una u otra de estas posiciones. Por ejemplo, los elementos de una matriz se numeran comenzando desde 0 en C, de modo que para una matriz de n elementos la secuencia de índices de matriz se ejecuta de 0 a n -1. Esto permite que se calcule la ubicación de un elemento de matriz al agregar el índice directamente a la dirección de la matriz, mientras que los lenguajes basados en 1 precalculan la dirección base de la matriz para que sea la posición un elemento antes que la primera.
Puede haber confusión entre la indexación basada en 0 y 1, por ejemplo, los parámetros de los índices JDBC de Java desde 1, aunque Java usa la indexación basada en 0.
En las bases de datos, es posible que un campo no tenga un valor. Entonces se dice que tiene un valor nulo. Para campos numéricos, no es el valor cero. Para los campos de texto, esto no está en blanco ni la cadena vacía. La presencia de valores nulos conduce a una lógica de tres valores. Ya no es una condición verdadera o falsa , pero puede ser indeterminada . Cualquier cálculo que incluya un valor nulo entrega un resultado nulo.
Un puntero nulo es un puntero en un programa de computadora que no apunta a ningún objeto o función. En C, la constante 0 entera se convierte en el puntero nulo en el momento de la compilación cuando aparece en un contexto de puntero, por lo que 0 es una forma estándar de referirse al puntero nulo en el código. Sin embargo, la representación interna del puntero nulo puede ser cualquier patrón de bit (posiblemente valores diferentes para diferentes tipos de datos).
En matemáticas -0 = +0 = 0; ambos -0 y +0 representan exactamente el mismo número, es decir, no existe un "cero positivo" o un "cero negativo" distinto de cero. Sin embargo, en algunas representaciones de números firmados de hardware, cero tiene dos representaciones distintas, una positiva agrupada con los números positivos y una negativa agrupada con los negativos; este tipo de representación dual se conoce como cero firmado, con la última forma a veces llamada cero negativo. Estas representaciones incluyen la magnitud firmada y las representaciones enteras binarias del complemento (pero no la forma binaria complementaria de los dos utilizada en la mayoría de las computadoras modernas) y la mayoría de las representaciones numéricas de coma flotante (como IEEE 754 e IBM S / 390 formatos de coma flotante).
En binario, 0 representa el valor de "apagado", lo que significa que no hay flujo de electricidad.
Cero es el valor de falso en muchos lenguajes de programación.
La época de Unix (la fecha y hora asociadas con una marca de tiempo cero) comienza la medianoche anterior al primero de enero de 1970.
La época de MacOS y la época de Palm OS (la fecha y hora asociadas a una marca de tiempo cero) comienza la medianoche anterior al primero de enero de 1904.
Muchas API y sistemas operativos que requieren que las aplicaciones devuelvan un valor entero como estado de salida suelen usar cero para indicar valores correctos y distintos de cero para indicar un error específico o condiciones de advertencia.
Otros campos
- En telefonía, presionar 0 se usa a menudo para marcar fuera de una red de la compañía o a una ciudad o región diferente, y 00 se usa para marcar en el extranjero. En algunos países, marcar 0 hace una llamada para obtener asistencia del operador.
- Los DVD que se pueden reproducir en cualquier región a veces se denominan "región 0"
- Las ruedas de ruleta suelen tener un espacio "0" (y algunas veces también un espacio "00"), cuya presencia se ignora al calcular los pagos (lo que permite que la casa gane a largo plazo).
- En la Fórmula Uno, si el actual Campeón del Mundo ya no compite en la Fórmula Uno en el año siguiente a su victoria en la carrera por el título, 0 se le otorga a uno de los pilotos del equipo con el que el campeón reinante ganó el título. Esto sucedió en 1993 y 1994, con Damon Hill conduciendo el auto 0, debido a que el actual Campeón del Mundo (Nigel Mansell y Alain Prostrespectively) no compite en el campeonato.
- En el sistema de autopistas interestatales de los EE. UU., En la mayoría de los estados, las salidas están numeradas según el poste de millas más cercano al extremo occidental o meridional de la carretera dentro de ese estado. Varios que están a menos de media milla (800 m) de los límites del estado en esa dirección se numeran como Salida 0.
Símbolos y representaciones
El dígito numérico moderno 0 generalmente se escribe como un círculo o elipse. Tradicionalmente, muchos tipos de letras de imprenta hacían que la letra mayúscula O fuera más redondeada que el dígito elíptico más angosto 0. Las máquinas de escribir originalmente no distinguían en forma entre O y 0; algunos modelos ni siquiera tenían una clave separada para el dígito 0. La distinción adquirió importancia en las pantallas de personajes modernos.
Se puede usar un cero reducido para distinguir el número de la letra. El dígito 0 con un punto en el centro parece haberse originado como una opción en las pantallas IBM 3270 y ha continuado con algunos tipos modernos de computadora como Andalé Mono y en algunos sistemas de reserva de líneas aéreas. Una variación usa una barra vertical corta en lugar del punto. Algunas fuentes diseñadas para usarse con computadoras hicieron que uno de los pares capital-O-digit-0 fuera más redondeado y el otro más angular (más cercano a un rectángulo). Se hace una distinción adicional en el tipo de letra que obstaculiza la falsificación, tal como se usa en las matrículas de automóviles alemanas, al abrir el dígito 0 en el lado superior derecho. A veces, el dígito 0 se usa exclusivamente o no se usa para evitar la confusión por completo.
Etiqueta del año
En la era del calendario de BC, el año 1 aC es el primer año antes de AD 1; no hay un año cero. Por el contrario, en la numeración astronómica de años, el año 1 aC está numerado 0, el año 2 aC está numerado -1, y así sucesivamente.