Teoría de los números
Definición
La teoría de números (o la aritmética o la aritmética superior en el uso de mayores), es una rama de las matemáticas puras dedicados principalmente al estudio de los números enteros. El matemático alemán Carl Friedrich Gauss (1777-1855) dijo: "Las matemáticas son la reina de las ciencias, y la teoría de los números es la reina de las matemáticas". Los teóricos numéricos estudian los números primos así como las propiedades de los objetos formados por enteros (por ejemplo, números racionales) o definidos como generalizaciones de los enteros (por ejemplo, enteros algebraicos).
Los enteros pueden considerarse en sí mismos o como soluciones a ecuaciones (geometría diofántica). Las preguntas en la teoría de números a menudo se entienden mejor mediante el estudio de objetos analíticos (por ejemplo, la función zeta de Riemann) que codifican propiedades de los enteros, primos u otros objetos teóricos numéricos de alguna manera (teoría del número analítico). También se pueden estudiar los números reales en relación con los números racionales, por ejemplo, aproximados por el último (aproximación diofántica).
El término más antiguo para teoría de números es la aritmética . A principios del siglo XX, había sido reemplazada por la "teoría de los números". (La palabra "aritmética" es usada por el público general para significar "cálculos elementales", también ha adquirido otros significados en lógica matemática, como en la aritmética de Peano , y en ciencias de la computación, como en la aritmética de punto flotante .) El uso del término la aritmética para la teoría de números recuperó algo de terreno en la segunda mitad del siglo XX, posiblemente en parte debido a la influencia francesa. En particular, se prefiere el aritméticocomo un adjetivo para teórico de números .
Historia
Orígenes
Amanecer de la aritmética
El primer hallazgo histórico de naturaleza aritmética es un fragmento de una tabla: la tableta de arcilla rota Plimpton 322 (Larsa, Mesopotamia, alrededor de 1800 aC) contiene una lista de "triples pitagóricos", es decir, enteros tales que . Los triples son demasiados y demasiado grandes para ser obtenidos por la fuerza bruta. El encabezado sobre la primera columna dice: "El takiltum de la diagonal que se ha restado de modo que el ancho ..."
El diseño de la tabla sugiere que fue construido por medio de lo que equivale, en lenguaje moderno, a la identidad
que está implícito en los viejos ejercicios de Babilonia. Si se usó algún otro método, las tripletas se construyeron primero y luego se reordenaron , presumiblemente para su uso real como una "tabla", es decir, con vistas a las aplicaciones.
No se sabe qué aplicaciones pueden haber sido o si podría haber sido alguna; La astronomía babilónica, por ejemplo, realmente se hizo realidad solo más tarde. En cambio, se sugirió que la mesa era una fuente de ejemplos numéricos para problemas escolares.
Mientras que la teoría de los números babilónicos -o lo que sobrevive de las matemáticas babilónicas que se puede llamar así- consiste en este único y sorprendente fragmento, el álgebra babilónica (en el sentido de "álgebra" de la escuela secundaria) estaba excepcionalmente bien desarrollada. Las fuentes neoplatónicas tardías afirman que Pitágoras aprendió las matemáticas de los babilonios. Muchas fuentes anteriores afirman que Tales y Pitágoras viajaron y estudiaron en Egipto.
Euclides IX 21-34 es muy probablemente pitagórico; es un material muy simple ("tiempos impares incluso es par", "si un número impar mide [= divide] un número par, entonces también mide [= divide] la mitad"), pero es todo lo que se necesita para demostrar que es irracional. Los místicos pitagóricos dieron gran importancia a lo extraño y lo par. El descubrimiento que es irracional se atribuye a los primeros pitagóricos (pre-Theodorus). Al revelar (en términos modernos) que los números pueden ser irracionales, este descubrimiento parece haber provocado la primera crisis fundacional en la historia matemática; su prueba o su divulgación se acreditan a veces a Hippasus, que fue expulsado o separado de la secta pitagórica. Esto forzó una distinción entre los números(enteros y los racionales, los sujetos de la aritmética), por una parte, y longitudes y proporciones (que identificaríamos con números reales, sean racionales o no), por otra parte.
La tradición pitagórica también habló de los llamados números poligonales o figurados. Mientras que los números cuadrados, números cúbicos, etc., se consideran ahora más naturales que los números triangulares, pentagonales, etc., el estudio de las sumas de números triangulares y pentagonales sería fructífero en el período moderno temprano (del siglo XVII al siglo XIX) )
No conocemos ningún material claramente aritmético en fuentes egipcias antiguas o védicas, aunque hay algo de álgebra en ambos. El teorema del resto chino aparece como un ejercicio en Sunzi Suanjing (3 °, 4 ° o 5 ° siglo EC). (Hay un paso importante pasado por alto en la solución de Sunzi: es el problema que luego fue resuelto por el Kuṭṭaka de Āryabhaṭa - ver abajo).
También hay algo de misticismo numérico en las matemáticas chinas, pero, a diferencia de los pitagóricos, parece que no condujo a ninguna parte. Al igual que los números perfectos de los pitagóricos, los cuadrados mágicos han pasado de la superstición a la recreación.
Grecia clásica y el período helenístico temprano
Aparte de unos pocos fragmentos, las matemáticas de la Grecia clásica son conocidas por nosotros a través de los informes de los no matemáticos contemporáneos o de las obras matemáticas del período helenístico temprano. En el caso de la teoría de números, esto significa, en general, Platón y Euclides , respectivamente.
Mientras que las matemáticas asiáticas influyeron en el aprendizaje griego y helenístico, parece ser el caso de que las matemáticas griegas también son una tradición indígena.
Eusebio, PE X, capítulo 4 menciona a Pitágoras:
Aristóteles afirmó que la filosofía de Platón siguió de cerca las enseñanzas de los pitagóricos, y Cicerón repite esta afirmación: Platonem ferunt didicisse Pythagorea omnia ("Dicen que Platón aprendió todas las cosas pitagóricas").
Platón tenía un gran interés en las matemáticas y distinguía claramente entre aritmética y cálculo. (Por aritmética quiso decir, en parte, teorizar sobre el número, más que lo que la aritmética o la teoría de los números han llegado a significar). Es a través de uno de los diálogos de Platón -a saber, Teeteto- que sabemos que Teodoro demostró que son irracionales. Teeteto era, como Platón, un discípulo de Teodoro; trabajó en la distinción de diferentes tipos de inconmensurables y, por lo tanto, podría decirse que fue un pionero en el estudio de los sistemas numéricos. (El libro X de los Elementos de Euclides es descrito por Pappus como basado en gran medida en el trabajo de Teeteto).
Euclides dedicó parte de sus Elementos a números primos y divisibilidad, temas que pertenecen sin ambigüedad a la teoría de números y que son básicos para ella (Libros VII a IX de los Elementos de Euclides). En particular, dio un algoritmo para calcular el mayor divisor común de dos números (el algoritmo euclidiano, Elementos , Prop. VII.2) y la primera prueba conocida de la infinitud de primos ( Elementos , Prop. IX.20).
En 1773, Lessing publicó un epigrama que había encontrado en un manuscrito durante su trabajo como bibliotecario; decía ser una carta enviada por Arquímedes a Eratóstenes. El epigrama propuso lo que se conoce como el problema del ganado de Arquímedes; su solución (ausente del manuscrito) requiere resolver una ecuación cuadrática indeterminada (que se reduce a lo que más tarde se llamaría incorrectamente la ecuación de Pell). Hasta donde sabemos, tales ecuaciones fueron tratadas con éxito por primera vez por la escuela india. No se sabe si el propio Archimedes tenía un método de solución.
Diofanto
Se sabe muy poco acerca de Diofanto de Alejandría; probablemente vivió en el siglo III EC, es decir, unos quinientos años después de Euclides. Seis de los trece libros de la Arithmetica de Diofanto sobreviven en el griego original; Cuatro libros más sobreviven en una traducción al árabe. La Aritmética es una colección de problemas resueltos donde la tarea consiste invariablemente en encontrar soluciones racionales a un sistema de ecuaciones polinómicas, generalmente de la forma o . Por lo tanto, hoy en día, hablamos de ecuaciones diofánticas cuando hablamos de ecuaciones polinomiales a las cuales se deben encontrar soluciones racionales o enteras.
Se puede decir que Diofanto estaba estudiando puntos racionales, es decir, puntos cuyas coordenadas son racionales, en curvas y variedades algebraicas; sin embargo, a diferencia de los griegos del período clásico, que hicieron lo que ahora llamaríamos álgebra básica en términos geométricos, Diofante hizo lo que ahora llamaríamos geometría algebraica básica en términos puramente algebraicos. En lenguaje moderno, lo que Diophantus hizo fue encontrar parametrizaciones racionales de las variedades; es decir, dada una ecuación de la forma (por ejemplo) , su objetivo era encontrar (en esencia) tres funciones racionales tales que, para todos los valores de y , establecer para da una solución a
Diophantus también estudió las ecuaciones de algunas curvas no racionales, para las cuales no es posible una parametrización racional. Se las arregló para encontrar algunos puntos racionales sobre estas curvas (curvas elípticas, como es el caso, en lo que parece ser su primera aparición conocida) por medio de lo que equivale a una construcción tangente: traducido en la geometría de coordenadas (que no existía en la época de Diofanto ), su método se visualizaría dibujando una tangente a una curva en un punto racional conocido, y luego encontrando el otro punto de intersección de la tangente con la curva; ese otro punto es un nuevo punto racional. (Diofanto también recurrió a lo que podría llamarse un caso especial de construcción secante).
Mientras que Diofanto estaba preocupado en gran medida con soluciones racionales, asumió algunos resultados en números enteros, en particular que cada entero es la suma de cuatro cuadrados (aunque nunca lo declaró explícitamente).
Āryabhaṭa, Brahmagupta, Bhāskara
Si bien la astronomía griega probablemente influyó en el aprendizaje indio, hasta el punto de introducir la trigonometría, parece ser el caso de que las matemáticas indias sean una tradición indígena; en particular, no hay evidencia de que los Elementos de Euclides llegaron a la India antes del siglo XVIII.
Āryabhaṭa (476-550 CE) mostró que los pares de congruencias simultáneas , podían ser resueltos por un método que él llamó kuṭṭaka , o pulverizador ; este es un procedimiento cercano a (una generalización de) el algoritmo euclidiano, que probablemente se descubrió independientemente en la India. Āryabhaṭa parece haber tenido en mente las aplicaciones a los cálculos astronómicos.
Brahmagupta (628 EC) comenzó el estudio sistemático de ecuaciones cuadráticas indefinidas, en particular, la mal llamada ecuación de Pell, en la que Arquímedes pudo haber estado interesado por primera vez, y que no comenzó a resolverse en Occidente hasta la época de Fermat y Euler. Los autores sánscritos posteriores seguirían, usando la terminología técnica de Brahmagupta. Un procedimiento general (el chakravala, o "método cíclico") para resolver la ecuación de Pell fue finalmente encontrado por Jayadeva (citado en el siglo XI, su trabajo se pierde de otra manera); la exposición más antigua que sobrevive aparece en Bīja-gaṇita de Bhāskara II (siglo XII).
Las matemáticas indias permanecieron en gran medida desconocidas en Europa hasta finales del siglo XVIII; El trabajo de Brahmagupta y Bhāskara fue traducido al inglés en 1817 por Henry Colebrooke.
Aritmética en la edad de oro islámica
A principios del siglo IX, el califa Al-Ma'mun ordenó traducciones de muchas obras matemáticas griegas y al menos una obra sánscrita (el Sindhind , que puede o no ser el Brāhmasphuṭasiddhānta de Brahmagupta). El trabajo principal de Diophantus, el Arithmetica , fue traducido al árabe por Qusta ibn Luqa (820-912). Parte del tratado al-Fakhri (por al-Karajī, 953 - alrededor de 1029) se basa en él hasta cierto punto. Según Rashed Roshdi, el contemporáneo de Al-Karajī Ibn al-Haytham sabía lo que más tarde se llamaría el teorema de Wilson.
Europa occidental en la Edad Media
Aparte de un tratado sobre cuadrados en la progresión aritmética de Fibonacci, que vivió y estudió en el norte de África y Constantinopla durante sus años formativos, ca. 1175-1200: no se habló de teoría de números para hablar de Europa occidental durante la Edad Media. Las cosas comenzaron a cambiar en Europa a finales del Renacimiento, gracias a un estudio renovado de las obras de la antigüedad griega. Un catalizador fue la corrección textual y la traducción al latín de la Arithmetica de Diofanto (Bachet, 1621, tras un primer intento de Xylander, 1575).
La teoría de los números modernos iniciales
Fermat
Pierre de Fermat (1601-1665) nunca publicó sus escritos; en particular, su trabajo sobre teoría de números está contenido casi en su totalidad en cartas a matemáticos y en notas marginales privadas. Escribió casi ninguna prueba en teoría de números; él no tenía modelos en el área. Hizo uso repetido de la inducción matemática, introduciendo el método del descenso infinito.
Uno de los primeros intereses de Fermat fueron los números perfectos (que aparecen en Euclides, Elementos IX) y los números amistosos; esto lo llevó a trabajar en divisores enteros, que fueron desde el principio entre los temas de la correspondencia (1636 en adelante) que lo pusieron en contacto con la comunidad matemática del momento. Ya había estudiado cuidadosamente la edición de Diofanto de Bachet; hacia 1643, sus intereses se habían desplazado en gran parte a problemas diofánticos y sumas de cuadrados (también tratados por Diofanto).
Los logros de Fermat en aritmética incluyen:
- El pequeño teorema de Fermat (1640), que establece que, si a no es divisible por un primo p , entonces
- Si a y b son coprime, entonces no es divisible por ningún primo congruente a -1 módulo 4; y cada primo congruente a 1 módulo 4 se puede escribir en la forma . Estas dos declaraciones también datan de 1640; en 1659, Fermat declaró a Huygens que había demostrado la última declaración por el método de la descendencia infinita. Fermat y Frenicle también hicieron algo de trabajo (algunos de ellos erróneos) en otras formas cuadráticas.
- Fermat planteó el problema de la resolución como un desafío para los matemáticos ingleses (1657). El problema fue resuelto en unos pocos meses por Wallis y Brouncker. Fermat consideró que su solución era válida, pero señaló que habían proporcionado un algoritmo sin una prueba (como lo habían hecho Jayadeva y Bhaskara, aunque Fermat nunca lo sabría). Él declara que una prueba se puede encontrar por descendencia.
- Fermat desarrolló métodos para (hacer lo que en nuestros términos equivale a) encontrar puntos en las curvas de los géneros 0 y 1. Al igual que en Diofanto, hay muchos procedimientos especiales y lo que equivale a una construcción tangente, pero no se usa una construcción secante.
- Fermat declara y prueba (por descenso) en el apéndice de Observaciones sobre Diophantus (Obs. XLV) que no tiene soluciones no triviales en los enteros. Fermat también mencionó a sus corresponsales que no tiene soluciones no triviales, y que esto podría ser probado por descendencia. La primera prueba conocida se debe a Euler (1753, de hecho por descendencia).
La afirmación de Fermat ("último teorema de Fermat") de haber demostrado que no hay soluciones para todos aparece solo en sus anotaciones al margen de su copia de Diofanto.
Euler
El interés de Leonhard Euler (1707-1783) en la teoría de los números se estimuló por primera vez en 1729, cuando un amigo suyo, el aficionado Goldbach, lo dirigió hacia algunos de los trabajos de Fermat sobre el tema. Esto se ha llamado el "renacimiento" de la teoría numérica moderna, después de la relativa falta de éxito de Fermat en llamar la atención de sus contemporáneos sobre el tema. El trabajo de Euler en teoría de números incluye lo siguiente:
- Pruebas para las declaraciones de Fermat. Esto incluye el pequeño teorema de Fermat (generalizado por Euler a módulos no primos); el hecho de que si y solo si ; trabajo inicial hacia una prueba de que cada entero es la suma de cuatro cuadrados (la primera prueba completa es de Joseph-Louis Lagrange (1770), pronto mejorado por el propio Euler); la falta de soluciones enteras distintas de cero (lo que implica el caso n = 4 del último teorema de Fermat, el caso n = 3 del cual Euler también lo demostró mediante un método relacionado).
- La ecuación de Pell , primera mal llamada por Euler. Escribió sobre el vínculo entre fracciones continuas y la ecuación de Pell.
- Primeros pasos hacia la teoría del número analítico. En su trabajo de sumas de cuatro cuadrados, particiones, números pentagonales y la distribución de números primos, Euler fue pionero en el uso de lo que se puede ver como análisis (en particular, series infinitas) en la teoría de números. Como vivió antes del desarrollo del análisis complejo, la mayor parte de su trabajo se limita a la manipulación formal de series de poder. Sin embargo, hizo algunos trabajos iniciales muy notables (aunque no totalmente rigurosos) sobre lo que más tarde se llamaría la función zeta de Riemann.
- Formas cuadráticas . Siguiendo el ejemplo de Fermat, Euler investigó más sobre la cuestión de qué primos se pueden expresar en la forma , algunos de ellos prefigurando la reciprocidad cuadrática.
- Ecuaciones diofánticas . Euler trabajó en algunas ecuaciones diofánticas de los géneros 0 y 1. En particular, estudió la obra de Diofanto; Trató de sistematizarlo, pero aún no era el momento adecuado para tal empeño: la geometría algebraica todavía estaba en su infancia. Se dio cuenta de que había una conexión entre los problemas diofánticos y las integrales elípticas, cuyo estudio él mismo había iniciado.
Lagrange, Legendre y Gauss
Joseph-Louis Lagrange (1736-1813) fue el primero en dar pruebas completas de algunos de los trabajos y observaciones de Fermat y Euler, por ejemplo, el teorema de cuatro cuadrados y la teoría básica de la mal llamada "ecuación de Pell" (para la cual un algoritmo solución fue encontrada por Fermat y sus contemporáneos, y también por Jayadeva y Bhaskara II antes que ellos.) También estudió las formas cuadráticas en generalidad completa (en oposición a ) - definiendo su relación de equivalencia, mostrando cómo ponerlas en forma reducida, etc.
Adrien-Marie Legendre (1752-1833) fue el primero en establecer la ley de la reciprocidad cuadrática. También conjeturó lo que equivale al teorema del número primo y el teorema de Dirichlet sobre las progresiones aritméticas. Dio un tratamiento completo de la ecuación y trabajó en formas cuadráticas a lo largo de las líneas desarrolladas posteriormente por Gauss. En su vejez, fue el primero en probar "el último teorema de Fermat" (completando el trabajo de Peter Gustav Lejeune Dirichlet, y acreditándolo a él y a Sophie Germain).
En su Disquisitiones Arithmeticae (1798), Carl Friedrich Gauss (1777-1855) demostró la ley de la reciprocidad cuadrática y desarrolló la teoría de las formas cuadráticas (en particular, definiendo su composición). También introdujo una notación básica (congruencias) y dedicó una sección a cuestiones computacionales, incluidas las pruebas de primalidad. La última sección de las Disquisitiones estableció un vínculo entre las raíces de la unidad y la teoría de los números:
De esta manera, se podría decir que Gauss hizo una primera incursión tanto en el trabajo de Évariste Galois como en la teoría de números algebraicos.
Madurez y división en subcampos
Comenzando a principios del siglo diecinueve, gradualmente ocurrieron los siguientes desarrollos:
- El aumento a la autoconciencia de la teoría de números (o aritmética superior ) como un campo de estudio.
- El desarrollo de gran parte de las matemáticas modernas necesarias para la teoría de números moderna básica: análisis complejo, teoría de grupos, teoría de Galois, acompañado por un mayor rigor en el análisis y la abstracción en álgebra.
- La subdivisión aproximada de la teoría de números en sus subcampos modernos, en particular, la teoría numérica analítica y algebraica.
Se puede decir que la teoría de los números algebraicos comienza con el estudio de la reciprocidad y la ciclotomía, pero realmente se hizo propia con el desarrollo del álgebra abstracta y la teoría ideal temprana y la teoría de la valoración; vea abajo. Un punto de partida convencional para la teoría del número analítico es el teorema de Dirichlet sobre las progresiones aritméticas (1837), cuya demostración introdujo funciones L e involucró algunos análisis asintóticos y un proceso limitante sobre una variable real. El primer uso de ideas analíticas en la teoría de números en realidad se remonta a Euler (1730), que utilizó series de poder formales y argumentos limitantes no rigurosos (o implícitos). El uso de complejo el análisis en la teoría de los números viene después: el trabajo de Bernhard Riemann (1859) sobre la función zeta es el punto de partida canónico; El teorema de cuatro cuadrados de Jacobi (1839), que lo antecede, pertenece a una cadena inicialmente diferente que ahora ha asumido un papel principal en la teoría del número analítico (formas modulares).
La historia de cada subcampo se aborda brevemente en su propia sección a continuación; ver el artículo principal de cada subcampo para tratamientos más completos. Muchas de las preguntas más interesantes en cada área permanecen abiertas y se están trabajando activamente en ellas.
Subdivisiones principales
Herramientas elementales
El término elemental generalmente denota un método que no usa análisis complejo. Por ejemplo, el teorema del número primo se probó por primera vez mediante análisis complejos en 1896, pero Erdős y Selberg encontraron una prueba elemental solo en 1949. El término es un tanto ambiguo: por ejemplo, las pruebas basadas en teoremas de Tauberian complejos (p. Ej., Wiener-Ikehara) a menudo se consideran esclarecedoras pero no elementales, a pesar de utilizar análisis de Fourier, en lugar de análisis complejos como tales. Aquí como en otros lugares, una prueba elementalpuede ser más larga y más difícil para la mayoría de los lectores que para una no elemental.
La teoría de los números tiene la reputación de ser un campo del que muchos de los resultados se pueden expresar al lego. Al mismo tiempo, las pruebas de estos resultados no son particularmente accesibles, en parte porque la gama de herramientas que utilizan es, en todo caso, inusualmente amplia dentro de las matemáticas.
Teoría analítica de números
La teoría de los números analíticos puede definirse
- en términos de sus herramientas, como el estudio de los enteros por medio de herramientas de análisis real y complejo; o
- en términos de sus preocupaciones, como el estudio dentro de la teoría numérica de estimaciones sobre el tamaño y la densidad, en oposición a las identidades.
Algunos temas generalmente considerados como parte de la teoría del número analítico, por ejemplo, la teoría tamizada, se cubren mejor con la segunda definición que con la primera: parte de la teoría tamiz, por ejemplo, usa poco análisis, pero pertenece a la teoría analítica de números.
Los siguientes son ejemplos de problemas en la teoría del número analítico: el teorema del número primo, la conjetura de Goldbach (o la conjetura de la gemela prima, o las conjeturas de Hardy-Littlewood), el problema de Waring y la hipótesis de Riemann. Algunas de las herramientas más importantes de la teoría del número analítico son el método del círculo, los métodos de tamizado y las funciones L (o, más bien, el estudio de sus propiedades). La teoría de las formas modulares (y, más en general, las formas automórficas) también ocupa un lugar cada vez más central en la caja de herramientas de la teoría de los números analíticos.
Uno puede hacer preguntas analíticas sobre números algebraicos, y usar medios analíticos para responder tales preguntas; es así como la teoría de números algebraicos y analíticos se cruzan. Por ejemplo, uno puede definir ideales primarios (generalizaciones de números primos en el campo de números algebraicos) y preguntar cuántos ideales primarios hay hasta cierto tamaño. Esta pregunta puede responderse mediante un examen de las funciones zeta de Dedekind, que son generalizaciones de la función zeta de Riemann, un objeto analítico clave en las raíces del sujeto. Este es un ejemplo de un procedimiento general en la teoría de números analíticos: derivar información sobre la distribución de una secuencia (aquí, ideales primos o números primos) del comportamiento analítico de una función de valores complejos construida apropiadamente.
Teoría de números algebraicos
Un número algebraico es cualquier número complejo que es una solución a alguna ecuación polinomial con coeficientes racionales; por ejemplo, cada solución de (digamos) es un número algebraico. Los campos de números algebraicos también se llaman campos de números algebraicos, o campos de números cortos . La teoría de números algebraicos estudia campos de números algebraicos. Por lo tanto, la teoría numérica analítica y algebraica puede y se superponen: la primera se define por sus métodos, la segunda por sus objetos de estudio.
Podría argumentarse que el tipo más simple de campos numéricos (viz., Campos cuadráticos) ya fue estudiado por Gauss, ya que la discusión de las formas cuadráticas en Disquisitiones arithmeticae puede replantearse en términos de ideales y normas en campos cuadráticos. (Un campo cuadrático consiste en todos los números de la forma , donde y son números racionales y es un número racional fijo cuya raíz cuadrada no es racional.) Por lo demás, el método chakravala del siglo XI asciende -en términos modernos- a un algoritmo para encontrar las unidades de un campo de número cuadrático real. Sin embargo, ni Bhāskara ni Gauss sabían de campos numéricos como tales.
Los fundamentos del tema tal como lo conocemos se establecieron a fines del siglo XIX, cuando se desarrollaron los números ideales , la teoría de los ideales y la teoría de la valoración ; Estas son tres formas complementarias de lidiar con la falta de factorización única en los campos de números algebraicos. (Por ejemplo, en el campo generado por los números racionales y , el número puede ser factorised tanto como y , todos , , y son irreducible, y por lo tanto, en un sentido ingenuo, análoga a primos entre los números enteros). El impulso inicial para el desarrollo de los números ideales (por Kummer) parece provenir del estudio de leyes de reciprocidad superiores, es decir, generalizaciones de la reciprocidad cuadrática.
Los campos numéricos se estudian a menudo como extensiones de campos de números más pequeños: un campo L se dice que es una extensión de un campo K Si L contiene K . (Por ejemplo, los números complejos C son una extensión de los reales R , y los reales R son una extensión de los racionales Q ). La clasificación de las posibles extensiones de un campo numérico dado es un problema difícil y parcialmente abierto. Extensiones abelianas, es decir, extensiones L de K tales que el grupo Galois Gal ( L / K ) de L sobre K es un grupo abeliano, son relativamente bien entendidos. Su clasificación fue el objeto del programa de teoría de campos de clase, que se inició a fines del siglo XIX (en parte por Kronecker y Eisenstein) y se llevó a cabo en gran parte en 1900-1950.
Un ejemplo de un área activa de investigación en teoría de números algebraicos es la teoría Iwasawa. El programa Langlands, uno de los principales planes actuales de investigación a gran escala en matemáticas, se describe a veces como un intento de generalizar la teoría de campos de clase a extensiones no abelianas de campos numéricos.
Geometría diofántica
El problema central de la geometría diofántica es determinar cuándo una ecuación de Diofantina tiene soluciones, y si lo hace, cuántas. El enfoque adoptado consiste en pensar en las soluciones de una ecuación como un objeto geométrico.
Por ejemplo, una ecuación en dos variables define una curva en el plano. De manera más general, una ecuación, o sistema de ecuaciones, en dos o más variables define una curva, una superficie o algún otro objeto en n -espacio dimensional. En la geometría diofántica, uno pregunta si hay puntos racionales (puntos cuyas coordenadas son racionales) o puntos integrales (puntos cuyas coordenadas son enteros) en la curva o superficie. Si hay tales puntos, el siguiente paso es preguntar cuántos hay y cómo se distribuyen. Una pregunta básica en esta dirección es: ¿hay finitos o infinitos puntos racionales en una curva (o superficie) dada? ¿Qué pasa con los puntos enteros?
Un ejemplo aquí puede ser útil. Considera la ecuación de Pitágoras ; nos gustaría estudiar sus soluciones racional, es decir, sus soluciones de tal manera que x y y son ambos racional. Esto es lo mismo que pedir todas las soluciones enteras ; cualquier solución a la última ecuación nos da una solución , a la primera. También es lo mismo que pedir todos los puntos con coordenadas racionales en la curva descrita por . (Esta curva pasa a ser un círculo de radio 1 alrededor del origen).
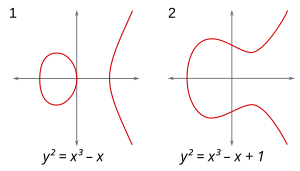
La reformulación de preguntas sobre ecuaciones en términos de puntos en curvas resulta afortunada. La finitud o no del número de puntos racionales o enteros en una curva algebraica, es decir, soluciones racionales o enteras para una ecuación , donde es un polinomio en dos variables, depende fundamentalmente del género de la curva. El género se puede definir de la siguiente manera: permite que las variables sean números complejos; luego define una superficie bidimensional en un espacio (proyectivo) de 4 dimensiones (ya que dos variables complejas pueden descomponerse en cuatro variables reales, es decir, cuatro dimensiones). Cuente el número de agujeros (rosarios) en la superficie; llamar a este número el género de . Otras nociones geométricas resultan ser tan cruciales.
También está el área estrechamente relacionada de las aproximaciones diofánticas: dado un número , ¿cuán bien pueden aproximarlo los racionales? (Estamos buscando aproximaciones que son buenas en relación con la cantidad de espacio que se necesita para escribir el racional: llamada (con ) una buena aproximación a si , donde es grande.) Esta pregunta es de especial interés si es un número algebraico. Si no se puede aproximar bien, entonces algunas ecuaciones no tienen soluciones enteras o racionales. Además, varios conceptos (especialmente el de la altura) resultan cruciales tanto en la geometría diofántica como en el estudio de las aproximaciones diofánticas. Esta pregunta también es de especial interés en la teoría de números trascendental: si un número se puede aproximar mejor que cualquier número algebraico, entonces es un número trascendental. Es por este argumento que
π y e han demostrado ser trascendentales.
π y e han demostrado ser trascendentales.
La geometría diofántica no debe confundirse con la geometría de los números, que es una colección de métodos gráficos para responder ciertas preguntas en la teoría de números algebraicos. La geometría aritmética , por otro lado, es un término contemporáneo para casi el mismo dominio que el cubierto por el término geometría diofántica . El término geometría aritmética se puede usar con más frecuencia cuando se desea enfatizar las conexiones con la geometría algebraica moderna (como, por ejemplo, el teorema de Faltings) más que con las técnicas en las aproximaciones diofánticas.
Enfoques y subcampos recientes
Las áreas que se muestran a continuación no datan de antes de mediados del siglo XX, incluso si se basan en material más antiguo. Por ejemplo, como se explica a continuación, la cuestión de los algoritmos en la teoría de los números es muy antigua, en cierto sentido más antigua que el concepto de prueba; al mismo tiempo, el estudio moderno de la computabilidad data solo de los años treinta y cuarenta, y la teoría de la complejidad computacional de los años setenta.
Teoría de números probabilísticos
Tome un número al azar entre uno y un millón. ¿Qué tan probable es ser primo? Esta es solo otra forma de preguntar cuántos primos hay entre uno y un millón. Además: ¿cuántos divisores principales tendrá, en promedio? ¿Cuántos divisores tendrá en total, y con qué probabilidad? ¿Cuál es la probabilidad de que tenga muchos o muchos menos divisores o divisores principales que el promedio?
Gran parte de la teoría probabilística de los números se puede considerar como un importante caso especial del estudio de variables que son casi, pero no exactamente, mutuamente independientes. Por ejemplo, el evento de que un entero aleatorio entre uno y un millón sea divisible por dos y el hecho de que sea divisible por tres sea casi independiente, pero no del todo.
A veces se dice que la combinatoria probabilística utiliza el hecho de que pase lo que pase con una probabilidad mayor que la que a veces ocurre; uno puede decir con igual justicia que muchas aplicaciones de la teoría de números probabilísticos dependen del hecho de que lo que sea inusual debe ser raro. Si ciertos objetos algebraicos (por ejemplo, soluciones racionales o enteras a ciertas ecuaciones) pueden mostrarse en la cola de ciertas distribuciones definidas con sensatez, se deduce que debe haber pocas; esta es una declaración no probabilística muy concreta seguida de una probabilística.
A veces, un enfoque probabilístico no riguroso conduce a una serie de algoritmos heurísticos y problemas abiertos, en particular la conjetura de Cramér.
Combinatoria aritmética
Deje A ser un conjunto de N enteros. Considere el conjunto A + A = { m + n | m , n ∈ A } que consiste en todas las sumas de dos elementos de A . ¿Es A + A mucho más grande que A ? ¿Apenas más grande? Si A + A es apenas más grande que A , debe A tener una gran cantidad de estructura aritmética, por ejemplo, ¿ A se asemeja a una progresión aritmética?
Si empezamos desde una bastante "gruesa" conjunto infinito , ¿contiene muchos elementos en progresión aritmética: , , digamos? ¿Debería ser posible escribir enteros grandes como sumas de elementos de ?
Estas preguntas son características de la combinatoria aritmética . Este es un campo actualmente coalescente; subsume la teoría del número aditivo (que se refiere a ciertos conjuntos muy específicos de significación aritmética, como los primos o los cuadrados) y, podría decirse, parte de la geometría de los números , junto con algún material nuevo de rápido desarrollo. Su enfoque en cuestiones de crecimiento y distribución se explica en parte por sus vínculos en desarrollo con la teoría ergódica, la teoría de grupos finitos, la teoría de modelos y otros campos. El término combinatoria aditiva también se usa; Sin embargo, los conjuntos no es necesario estudiar conjuntos de enteros, sino más bien subconjuntos de grupos no conmutativos, para los cuales se usa tradicionalmente el símbolo de multiplicación, no el símbolo de suma; también pueden ser subconjuntos de anillos, en cuyo caso el crecimiento de • y puede ser comparado.
Cálculos en teoría de números
Mientras que la palabra algoritmo se remonta solo a ciertos lectores de al-Khwārizmī, las descripciones cuidadosas de los métodos de solución son más antiguas que las pruebas: tales métodos (es decir, algoritmos) son tan antiguos como cualquier matemática reconocible: antiguo egipcio, babilónico, védico, chino -Siempre que las pruebas aparecieron solo con los griegos del período clásico. Un caso temprano interesante es el de lo que ahora llamamos el algoritmo euclidiano. En su forma básica (es decir, como un algoritmo para calcular el mayor divisor común) aparece como Proposición 2 del Libro VII en Elementos , junto con una prueba de corrección. Sin embargo, en la forma que se usa a menudo en teoría de números (a saber, como un algoritmo para encontrar soluciones enteras a una ecuación) , o, lo que es lo mismo, para encontrar las cantidades cuya existencia está asegurada por el teorema del resto chino) aparece por primera vez en los trabajos de Āryabhaṭa (siglo 5º-VI dC) como un algoritmo llamado kuṭṭaka("pulverizador"), sin una prueba de corrección
Hay dos preguntas principales: "¿podemos calcular esto?" y "¿podemos calcularlo rápidamente?". Cualquiera puede probar si un número es primo o, si no lo es, dividirlo en factores primos; hacerlo tan rápido es otro asunto. Ahora conocemos algoritmos rápidos para probar la primalidad, pero, a pesar de mucho trabajo (tanto teórico como práctico), no existe un algoritmo verdaderamente rápido para factorizar.
La dificultad de un cálculo puede ser útil: los protocolos modernos para cifrar mensajes (por ejemplo, RSA) dependen de funciones que son conocidas por todos, pero cuyas inversas (a) son conocidas solo por unos pocos elegidos, y (b) también lo tomarían. mucho tiempo para descubrirlo por cuenta propia. Por ejemplo, estas funciones pueden ser tales que sus inversas se pueden calcular solo si se han factorizado ciertos enteros grandes. Si bien se conocen muchos problemas de computación difíciles fuera de la teoría numérica, la mayoría de los protocolos de cifrado que funcionan hoy en día se basan en la dificultad de algunos problemas teóricos numéricos.
En una nota diferente: algunas cosas pueden no ser computables en absoluto; de hecho, esto puede ser probado en algunos casos. Por ejemplo, en 1970, se demostró, como solución al décimo problema de Hilbert, que no existe una máquina de Turing que pueda resolver todas las ecuaciones diofánticas. En particular, esto significa que, dado un conjunto computable de axiomas, existen ecuaciones diofánticas para las cuales no hay pruebas, a partir de los axiomas, de si el conjunto de ecuaciones tiene o no soluciones enteras. (Necesariamente estaríamos hablando de ecuaciones diofánticas para las cuales no hay soluciones enteras, ya que, dada una ecuación diofántica con al menos una solución, la solución en sí misma proporciona una prueba del hecho de que existe una solución. No podemos probar, por supuesto, que una ecuación diofántica particular es de este tipo,
Aplicaciones
El teórico de los números Leonard Dickson (1874-1954) dijo "Gracias a Dios que la teoría de los números no está mancillada por ninguna aplicación". Tal visión ya no es aplicable a la teoría de números. En 1974, Donald Knuth dijo: "... prácticamente cada teorema de la teoría de números elemental surge de una manera natural y motivada en relación con el problema de hacer que las computadoras realicen cálculos numéricos de alta velocidad". La teoría de los números elementales se enseña en cursos discretos de matemáticas para científicos informáticos; por otro lado, la teoría de números también tiene aplicaciones al continuo en el análisis numérico. Además de las conocidas aplicaciones para la criptografía, también existen aplicaciones para muchas otras áreas de las matemáticas.
Premios
La Sociedad Americana de Matemáticas otorga el Premio Cole en Teoría de Números . Además, la teoría de números es una de las tres subdisciplinas matemáticas premiadas por el Premio Fermat .