Wikiblog Cultulandia [es]

Un número complejo se puede representar visualmente como un par de números

(a, b) que

forman un vector en un diagrama llamado diagrama Argand, que representa el plano complejo. "Re" es el eje real, "Im" es el eje imaginario, y

i

satisface

i = -1

.

Un número complejo es un número que se puede expresar en la forma

a + bi

, donde

a

y

b

son números reales, y

i

es una solución de la ecuación

x = -1

. Debido a que ningún número real satisface esta ecuación,

i

se llama un número imaginario. Para el número complejo

a + bi

,

a

se llama la parte real , y

b

se llama la parte imaginaria. A pesar de la nomenclatura histórica "imaginaria", los números complejos son considerados en las ciencias matemáticas tan "reales" como los números reales, y son fundamentales en muchos aspectos de la descripción científica del mundo natural.

El sistema numérico complejo se puede definir como la extensión algebraica de los números reales ordinarios mediante un número imaginario

i

. Esto significa que los números complejos se pueden sumar, restar y multiplicar, como polinomios en la variable

i

, con la regla

i = -1

impuesta. Además, los números complejos también se pueden dividir por números complejos distintos de cero. En general, el sistema de números complejos es un campo.

Lo más importante es que los números complejos dan lugar al teorema fundamental del álgebra: toda ecuación polinomial no constante con coeficientes complejos tiene una solución compleja. Esta propiedad es verdadera de los números complejos, pero no de los reales. Al matemático italiano del siglo XVI, Gerolamo Cardano, se le acredita la introducción de números complejos en sus intentos de encontrar soluciones a las ecuaciones cúbicas.

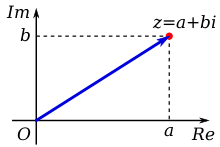
Geométricamente, los números complejos extienden el concepto de la línea numérica unidimensional al plano complejo bidimensional utilizando el eje horizontal para la parte real y el eje vertical para la parte imaginaria. El número complejo

a + bi

se puede identificar con el punto

(a, b)

en el plano complejo. Se dice que un número complejo cuya parte real es cero es puramente imaginario; los puntos para estos números se encuentran en el eje vertical del plano complejo. Un número complejo cuya parte imaginaria es cero se puede ver como un número real; su punto se encuentra en el eje horizontal del plano complejo. Los números complejos también se pueden representar en forma polar, que asocia cada número complejo con su distancia desde el origen (su magnitud) y con un ángulo particular conocido como el argumento de este número complejo.

Visión de conjunto

Los números complejos permiten soluciones a ciertas ecuaciones que no tienen soluciones en números reales. Por ejemplo, la ecuación

{\ displaystyle (x + 1) ^ {2} = - 9}

no tiene una solución real, ya que el cuadrado de un número real no puede ser negativo. Los números complejos proporcionan una solución a este problema. La idea es extender los números reales con una

i

indeterminada (a veces llamada la unidad imaginaria) que se toma para satisfacer la relación

i = -1

, de modo que se puedan encontrar soluciones a ecuaciones como la anterior. En este caso, las soluciones son

-1 + 3 i

y

-1 - 3 i

, como se puede verificar utilizando el hecho de que

i = -1

:

((-1 + 3i) +1) ^ {2} = (3i) ^ {2} = (3 ^ {2}) (i ^ {2}) = 9 (-1) = - 9,

((-1-3i) +1) ^ {2} = (- 3i) ^ {2} = (- 3) ^ {2} (i ^ {2}) = 9 (-1) = - 9.

De acuerdo con el teorema fundamental del álgebra, todas las ecuaciones polinómicas con coeficientes reales o complejos en una sola variable tienen una solución en números complejos.

Definición

Una ilustración del plano complejo. La parte real de un número complejo

z = x + iy

es

x

, y su parte imaginaria es

y

.

Un número complejo es un número de la forma

a + bi

, donde

a

y

b

son números reales e

i

es una satisfacción indeterminada

i = -1

. Por ejemplo,

2 + 3 i

es un número complejo.

Por lo tanto, un número complejo puede definirse como un polinomio en el único indeterminado

i

, con la relación

i + 1 = 0

impuesto. A partir de esta definición, los números complejos se pueden agregar o multiplicar, usando la suma y la multiplicación para polinomios. Formalmente, el conjunto de números complejos es el anillo de cociente del anillo polinómico en el indeterminado

i

, por el ideal generado por el polinomio

i + 1

(ver abajo). El conjunto de todos los números complejos se denota con (verticalmente en negrita) o (pizarra negrita).

\ mathbf {C}

\ mathbb {C}

El número real

a

se llama la parte real del número complejo

a + bi

; el número real

b

se llama la parte imaginaria de

a + bi

. Según esta convención, la parte imaginaria no incluye un factor de

i

: por lo tanto ,

b

, no

bi

, es la parte imaginaria. La parte real de un número complejo

z

se denota por

Re (z)

o

ℜ (z)

; la parte imaginaria de un número complejo

z

se denota por

Im (z)

o

ℑ (z)

. Por ejemplo,

{\ displaystyle {\ begin {aligned} \ operatorname {Re} (2 + 3i) & = 2 \\\ operatorname {Im} (2 + 3i) & = 3. \ end {aligned}}}

Un número real

a

puede considerarse como un número complejo

a + 0 i

cuya parte imaginaria es 0. Un número puramente imaginario

bi

es un número complejo

0 + bi

cuya parte real es cero. Es común escribir

una

para

un + 0 i

y

bi

por

0 + bi

. Además, cuando la parte imaginaria es negativa, es común escribir

a - bi

con

b > 0 en

lugar de

a + (- b) i

, por ejemplo

3 - 4 i

en lugar de

3 + (-4) i

.

Forma cartesiana y definición a través de pares ordenados

Por lo tanto, un número complejo puede identificarse con un par ordenado

(Re (z), Im (z))

en el plano cartesiano, una identificación a veces conocida como la forma cartesiana de

z

. De hecho, un número complejo se puede definir como un par ordenado

(a, b)

, pero las reglas para la suma y la multiplicación también se deben incluir como parte de la definición (ver a continuación). William Rowan Hamilton introdujo este enfoque para definir el sistema numérico complejo.

Plano complejo

Figura 1: Un número complejo z , trazado como un punto (rojo) y vector de posición (azul) en un diagrama de Argand;

a + b i

es su expresión rectangular .

Un número complejo se puede ver como un punto o vector de posición en un sistema cartesiano bidimensional de coordenadas llamado plano complejo o diagrama Argand (ver Pedoe 1988 y Solomentsev 2001), llamado así por Jean-Robert Argand. Los números se trazan convencionalmente usando la parte real como componente horizontal y la parte imaginaria como vertical (ver Figura 1). Estos dos valores utilizados para identificar un número complejo dado se denominan, por lo tanto, su forma cartesiana , rectangular o algebraica .

Un vector de posición también se puede definir en términos de su magnitud y dirección con respecto al origen. Estos se enfatizan en la forma polar de un número complejo . Usar la forma polar del número complejo en los cálculos puede conducir a una interpretación más intuitiva de los resultados matemáticos. Notablemente, las operaciones de suma y multiplicación adquieren un carácter geométrico muy natural cuando los números complejos se consideran vectores de posición: la suma corresponde a la suma del vector, mientras que la multiplicación corresponde a multiplicar sus magnitudes y agregar sus argumentos (es decir, los ángulos que hacen con el eje x ) Visto de esta manera la multiplicación de un número complejo por

i

corresponde a girar el vector de posición en sentido antihorario por un cuarto de vuelta (90 °) sobre el origen:

(a + b i) i

=

a i + b i

=

-b + a i

.

Historia en breve

Sección principal: Historia

La solución en radicales (sin funciones trigonométricas) de una ecuación cúbica general contiene las raíces cuadradas de los números negativos cuando las tres raíces son números reales, una situación que no puede ser rectificada por factoraje ayudado por la prueba de raíz racional si el cúbico es irreductible (el llamado casus irreducibilis). Este enigma llevó al matemático italiano Gerolamo Cardano a concebir números complejos alrededor de 1545, aunque su comprensión era rudimentaria.

El trabajo sobre el problema de los polinomios generales finalmente condujo al teorema fundamental del álgebra, que muestra que con números complejos, existe una solución para cada ecuación polinómica de grado uno o más. Los números complejos forman así un campo algebraicamente cerrado, donde cualquier ecuación polinomial tiene una raíz.

Muchos matemáticos contribuyeron al desarrollo completo de números complejos. Las reglas para la suma, la resta, la multiplicación y la división de números complejos fueron desarrolladas por el matemático italiano Rafael Bombelli. Un formalismo más abstracto para los números complejos fue desarrollado por el matemático irlandés William Rowan Hamilton, quien extendió esta abstracción a la teoría de los cuaterniones.

Notación

Debido a que es un polinomio en la indeterminada

i

,

un + ib

puede escribirse en lugar de

un + bi

, que a menudo es conveniente cuando

b

es un radical. En algunas disciplinas, en particular electromagnetismand eléctrica ingeniería,

j

se utiliza en lugar de

i

, ya que

i

se utiliza con frecuencia para la corriente eléctrica. En estos casos, los números complejos se escriben como

a + bj

o

a + jb

.

Relaciones de igualdad y orden

Dos números complejos son iguales si y solo si ambas partes, real e imaginaria, son iguales. Es decir, números complejos y son iguales si y solo si y . Si los números complejos están escritos en forma polar, son iguales si y solo si tienen el mismo argumento y la misma magnitud.

z_ {1}

z_ {2}

{\ displaystyle \ operatorname {Re} (z_ {1}) = \ operatorname {Re} (z_ {2})}

{\ displaystyle \ operatorname {Im} (z_ {1}) = \ operatorname {Im} (z_ {2})}

Debido a que los números complejos se consideran naturalmente como existentes en un plano bidimensional, no existe un ordenamiento lineal natural en el conjunto de números complejos. Además, no existe un orden lineal en los números complejos que sea compatible con la suma y la multiplicación: los números complejos no pueden tener la estructura de un campo ordenado. Esto se debe a que cualquier cuadrado en un campo ordenado es al menos

0

, pero

i = -1

.

Operaciones elementales

Conjugado

Representación geométrica de

zy

su conjugado en el plano complejo

{\ overline {z}}

El complejo conjugado del número complejo

z = x + yi

se define como

x - yi

. Se denota por una o

z

*

.

{\ overline {z}}

Geométricamente, es el "reflejo" de

z

sobre el eje real. Conjugar dos veces da el número complejo original:

{\ overline {z}}

{\ displaystyle {\ overline {\ overline {z}}} = z.}

Las partes real e imaginaria de un número complejo

z

se pueden extraer utilizando el conjugado:

{\ displaystyle \ operatorname {Re} (z) = {\ dfrac {z + {\ overline {z}}} {2}},}

{\ displaystyle \ operatorname {Im} (z) = {\ dfrac {z - {\ overline {z}}} {2i}}.}

Además, un número complejo es real si y solo si es igual a su propio conjugado.

La conjugación se distribuye sobre las operaciones aritméticas estándar:

{\ displaystyle {\ overline {z + w}} = {\ overline {z}} + {\ overline {w}},}

{\ displaystyle {\ overline {zw}} = {\ overline {z}} - {\ overline {w}},}

{\ displaystyle {\ overline {z \ cdot w}} = {\ overline {z}} \ cdot {\ overline {w}},}

{\ displaystyle {\ overline {z / w}} = {\ overline {z}} / {\ overline {w}}.}

Adición y sustracción

La suma de dos números complejos se puede hacer geométricamente construyendo un paralelogramo.

Los números complejos se agregan al agregar por separado las partes real e imaginaria de los sumandos. Es decir:

(a + bi) + (c + di) = (a + c) + (b + d) i. \

Del mismo modo, la resta se define por

(a + bi) - (c + di) = (ac) + (bd) i. \

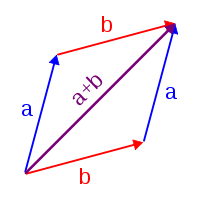
Usando la visualización de números complejos en el plano complejo, la suma tiene la siguiente interpretación geométrica: la suma de dos números complejos A y B , interpretados como puntos del plano complejo, es el punto X obtenido al construir un paralelogramo, tres de cuyos vértices son O , A y B . Equivalentemente, X es el punto tal que los triángulos con los vértices O , A , B y X , B , A , son congruentes.

Multiplicación y división

La multiplicación de dos números complejos se define por la siguiente fórmula:

(a + bi) (c + di) = (ac-bd) + (bc + ad) i. \

En particular, el cuadrado de

i

es -1:

i ^ {2} = i \ veces i = -1. \

La definición precedente de multiplicación de números complejos generales se deriva naturalmente de esta propiedad fundamental de

i

. En efecto, si

i

es tratado como un número de modo que

di

significa

d

veces

i

, la regla de la multiplicación anterior es idéntica a la regla habitual para la multiplicación de dos sumas de dos términos.

(a + bi) (c + di) = ac + bci + adi + bidi

(Propiedad distributiva)

= ac + bidi + bci + adi

(propiedad conmutativa de adición: el orden de los sumandos se puede cambiar)

= ac + bdi ^ {2} + (bc + ad) i

(propiedades conmutativas y distributivas)

{\ displaystyle = (ac-bd) + (bc + ad) i}

(propiedad fundamental de

i

).

La división de dos números complejos se define en términos de multiplicación compleja, que se describe arriba, y división real. Cuando al menos uno de

c

y

d

no es cero, tenemos

{\ displaystyle {\ frac {a + bi} {c + di}} = \ left ({ac + bd \ over c ^ {2} + d ^ {2}} \ right) + \ left ({bc-ad \ over c ^ {2} + d ^ {2}} \ right) i.}

La división se puede definir de esta manera debido a la siguiente observación:

{\ displaystyle {\ frac {a + bi} {c + di}} = {\ frac {\ left (a + bi \ right) \ cdot \ left (c-di \ right)} {\ left (c + di) \ right) \ cdot \ left (c-di \ right)}} = \ left ({ac + bd \ over c ^ {2} + d ^ {2}} \ right) + \ left ({bc-ad \ sobre c ^ {2} + d ^ {2}} \ right) i.}

Como se mostró anteriormente,

c - di

es el conjugado complejo del denominador

c + di

. Al menos una de la parte real

c

y la parte imaginaria

d

del denominador deben ser distintas de cero para que se defina la división. Esto se llama "racionalización" del denominador (aunque el denominador en la expresión final podría ser un número real irracional).

Recíproco

El recíproco de un número complejo distinto de cero

z = x + yi

viene dado por

{\ displaystyle {\ frac {1} {z}} = {\ frac {\ overline {z}} {z {\ overline {z}}}} = {\ frac {\ overline {z}} {x ^ { 2} + y ^ {2}}} = {\ frac {x} {x ^ {2} + y ^ {2}}} - {\ frac {y} {x ^ {2} + y ^ {2} }}yo.}

Esta fórmula se puede usar para calcular el inverso multiplicativo de un número complejo si se da en coordenadas rectangulares. La geometría inversa, una rama de la geometría que estudia reflexiones más generales que las de una línea, también se puede expresar en términos de números complejos. En el análisis de red de circuitos eléctricos, el conjugado complejo se usa para encontrar la impedancia equivalente cuando se usa el teorema de transferencia máxima de potencia.

Raíz cuadrada

Las raíces cuadradas de

a + bi

(con

b \neq 0

) son , donde

\ pm (\ gamma + \ delta i)

\ gamma = {\ sqrt {\ frac {a + {\ sqrt {a ^ {2} + b ^ {2}}}} {2}}}

y

\ delta = \ operatorname {sgn} (b) {\ sqrt {\ frac {-a + {\ sqrt {a ^ {2} + b ^ {2}}}} {2}}},

donde sgn es la función signum. Esto se puede ver al cuadrar para obtener

a

+

bi

. Aquí se llama el módulo de

a

+

bi

, y el signo de raíz cuadrada indica la raíz cuadrada con una parte real no negativa, llamada raíz cuadrada principal ; también donde

\ pm (\ gamma + \ delta i)

{\ sqrt {a ^ {2} + b ^ {2}}}

{\ displaystyle {\ sqrt {a ^ {2} + b ^ {2}}} = {\ sqrt {z {\ overline {z}}}},}

{\ displaystyle z = a + bi.}

Forma polar

Figura 2: El argumento

φ

y el módulo

r

ubican un punto en un diagrama de Argand; o son expresiones polares del punto.

r (\ cos \ varphi + i \ sin \ varphi)

re ^ {i \ varphi}

Valor y argumento absolutos

Una forma alternativa de definir un punto P en el plano complejo, además de usar las coordenadas x e y , es usar la distancia del punto desde O , el punto cuyas coordenadas son

(0, 0)

(el origen), junto con el ángulo subtendido entre el eje real positivo y el segmento de línea OP en sentido antihorario. Esta idea conduce a la forma polar de números complejos.

El valor absoluto (o módulo o magnitud ) de un número complejo

z = x + yi

es

{\ displaystyle r = | z | = {\ sqrt {x ^ {2} + y ^ {2}}}.}

Si

z

es un número real (es decir, si

y = 0

), entonces

r = | x |

. Es decir, el valor absoluto de un número real es igual a su valor absoluto como un número complejo.

Según el teorema de Pitágoras, el valor absoluto del número complejo es la distancia al origen del punto que representa el número complejo en el plano complejo.

El cuadrado del valor absoluto es

{\ displaystyle | z | ^ {2} = z {\ overline {z}} = x ^ {2} + y ^ {2}.}

¿Dónde está el complejo conjugado de

{\ overline {z}}

z

El argumento de

z

(en muchas aplicaciones referido como la "fase") es el ángulo del radio OP con el eje real positivo, y se escribe como . Al igual que con el módulo, el argumento se puede encontrar desde la forma rectangular :

\ arg (z)

x + yi

{\ displaystyle \ varphi = \ arg (z) = {\ begin {cases} \ arctan \ left ({\ dfrac {y} {x}} \ right) & {\ text {if}} x> 0 \\\ arctan \ left ({\ dfrac {y} {x}} \ right) + \ pi & {\ text {if}} x <0 {\ text {and}} y \ geq 0 \\\ arctan \ left ({ \ dfrac {y} {x}} \ right) - \ pi & {\ text {if}} x <0 {\ text {and}} y <0 \\ {\ dfrac {\ pi} {2}} & {\ text {if}} x = 0 {\ text {and}} y> 0 \\ - {\ dfrac {\ pi} {2}} & {\ text {if}} x = 0 {\ text {y }} y <0 \\ {\ text {indeterminate}} & {\ text {if}} x = 0 {\ text {and}} y = 0. \ end {cases}}}

Visualización de las raíces cuadradas a sextas de un número complejo z , en forma polar re donde φ = arg z y r = | z | - si z es real, φ = 0 o

π

. Las raíces principales están en negro.

Normalmente, como se indicó anteriormente, se elige el valor principal en el intervalo

(-π, π)

. Los valores en el rango

[0,2π)

se obtienen sumando

2π

si el valor es negativo. El valor de

φ

se expresa en radianes en este artículo. Puede aumentar en cualquier múltiplo entero de

2π

y aún así dar el mismo ángulo. Por lo tanto, la función arg a veces se considera multivalorada. El ángulo polar para el número complejo 0 es indeterminado, pero la elección arbitraria del ángulo 0 es común.

El valor de

φ

es igual al resultado de atan2:

{\ displaystyle \ varphi = \ operatorname {atan2} \ left (\ operatorname {Im} (z), \ operatorname {Re} (z) \ right).}

Juntos,

r

y

φ

dan otra forma de representar números complejos, la forma polar , ya que la combinación de módulo y argumento especifica completamente la posición de un punto en el plano. La recuperación de las coordenadas rectangulares originales de la forma polar se realiza mediante la fórmula llamada forma trigonométrica

{\ displaystyle z = r (\ cos \ varphi + i \ sin \ varphi).}

Usando la fórmula de Euler esto puede escribirse como

{\ displaystyle z = re ^ {i \ varphi}.}

Usando la función cis, esto a veces se abrevia a

{\ displaystyle z = r \ operatorname {cis} \ varphi.}

En la notación de ángulo, que se usa a menudo en electrónica para representar un fasor con amplitud

r

y fase

φ

, se escribe como

{\ displaystyle z = r \ angle \ varphi.}

Multiplicación y división en forma polar

Multiplicación de

2 + i

(triángulo azul) y

3 + i

(triángulo rojo). El triángulo rojo se gira para que coincida con el vértice del azul y se estira con
√
5 , la longitud de la hipotenusa del triángulo azul.

Las fórmulas para la multiplicación, división y exponenciación son más simples en forma polar que las fórmulas correspondientes en coordenadas cartesianas. Dado dos números complejos

z 1 = r 1 (cos φ 1 + i sen φ 1)

y

z 2 = r 2 (cos φ 2 + i sen φ 2)

, debido a las bien conocidas identidades trigonométricas

\ cos (a) \ cos (b) - \ sin (a) \ sin (b) = \ cos (a + b)

\ cos (a) \ sin (b) + \ sin (a) \ cos (b) = \ sin (a + b)

podemos derivar

{\ displaystyle z_ {1} z_ {2} = r_ {1} r_ {2} (\ cos (\ varphi _ {1} + \ varphi _ {2}) + i \ sin (\ varphi _ {1} + \ varphi _ {2})).}

En otras palabras, los valores absolutos se multiplican y los argumentos se agregan para producir la forma polar del producto. Por ejemplo, multiplicar por

i

corresponde a un cuarto de vuelta en sentido antihorario, que devuelve

i = -1

. La imagen de la derecha ilustra la multiplicación de

{\ displaystyle (2 + i) (3 + i) = 5 + 5i.}

Como la parte real e imaginaria de

5 + 5 i

es igual, el argumento de ese número es 45 grados, o π / 4 (en radianes). Por otro lado, también es la suma de los ángulos en el origen de los triángulos rojo y azul arctan (1/3) y arctan (1/2), respectivamente. Por lo tanto, la fórmula

{\ frac {\ pi} {4}} = \ arctan {\ frac {1} {2}} + \ arctan {\ frac {1} {3}}

sostiene. Como la función arctan se puede aproximar de manera altamente eficiente, fórmulas como esta, conocidas como fórmulas tipo Machin, se usan para aproximaciones de alta precisión de π.

Del mismo modo, la división está dada por

{\ frac {z_ {1}} {z_ {2}}} = {\ frac {r_ {1}} {r_ {2}}} \ left (\ cos (\ varphi _ {1} - \ varphi _ { 2}) + i \ sin (\ varphi _ {1} - \ varphi _ {2}) \ right).

Exponenciación

Fórmula de Euler

La fórmula de Euler establece que, para cualquier número real

x

,

e ^ {ix} = \ cos x + i \ sin x \

,

donde

e

es la base del logaritmo natural. Esto puede demostrarse por inducción al observar que

{\ begin {aligned} i ^ {0} & {} = 1, \ quad & i ^ {1} & {} = i, \ quad & i ^ {2} & {} = - 1, \ quad & i ^ {3 } & {} = - i, \\ i ^ {4} & = {} 1, \ quad & i ^ {5} & = {} i, \ quad & i ^ {6} & {} = - 1, \ quad & i ^ {7} & {} = - i, \ end {aligned}}

y así sucesivamente, y al considerar las expansiones de la serie Taylor de

e

,

cos x

y

sin x

:

{\ begin {aligned} e ^ {ix} & {} = 1 + ix + {\ frac {(ix) ^ {2}} {2!}} + {\ frac {(ix) ^ {3}} {3 !}} + {\ frac {(ix) ^ {4}} {4!}} + {\ frac {(ix) ^ {5}} {5!}} + {\ frac {(ix) ^ {6 }} {6!}} + {\ Frac {(ix) ^ {7}} {7!}} + {\ Frac {(ix) ^ {8}} {8!}} + \ Cdots \\ [8pt ] & {} = 1 + ix - {\ frac {x ^ {2}} {2!}} - {\ frac {ix ^ {3}} {3!}} + {\ Frac {x ^ {4} } {4!}} + {\ Frac {ix ^ {5}} {5!}} - {\ frac {x ^ {6}} {6!}} - {\ frac {ix ^ {7}} { 7!}} + {\ Frac {x ^ {8}} {8!}} + \ Cdots \\ [8pt] & {} = \ left (1 - {\ frac {x ^ {2}} {2! }} + {\ frac {x ^ {4}} {4!}} - {\ frac {x ^ {6}} {6!}} + {\ frac {x ^ {8}} {8!}} - \ cdots \ right) + i \ left (x - {\ frac {x ^ {3}} {3!}} + {\ frac {x ^ {5}} {5!}} - {\ frac {x ^ {7}} {7!}} + \ Cdots \ right) \\ [8pt] & {} = \ cos x + i \ sin x \. \ End {aligned}}

La reorganización de términos se justifica porque cada serie es absolutamente convergente.

Logaritmo natural

De la fórmula de Euler se deduce que, para cualquier número complejo z escrito en forma polar,

{\ displaystyle z = r (\ cos \ varphi + i \ sin \ varphi)}

donde r es un número real no negativo, un posible valor para el logaritmo complejo de z es

{\ displaystyle \ ln (z) = \ ln (r) + \ varphi i.}

Debido a que el coseno y el seno son funciones periódicas, se pueden obtener otros valores posibles. Por ejemplo,, entonces ambos y son dos valores posibles para el logaritmo natural de .

{\ displaystyle e ^ {i \ pi} = e ^ {3i \ pi} = - 1}

{\ displaystyle i \ pi}

{\ displaystyle 3i \ pi}

-1

Para tratar con la existencia de más de un valor posible para una entrada dada, el logaritmo complejo puede considerarse una función multivaluada, con

{\ displaystyle \ ln (z) = \ left \ {\ ln (r) + (\ varphi +2 \ pi k) i \; | \; k \ in \ mathbb {Z} \ right \}.}

Alternativamente, se puede usar un corte de rama para definir una "rama" de un solo valor del logaritmo complejo.

Exponentes enteros y fraccionarios

Podemos usar la identidad

\ ln (a ^ {b}) = b \ ln (a)

para definir la exponenciación compleja, que también tiene múltiples valores:

{\ displaystyle {\ begin {aligned} \ ln (z ^ {n}) & = \ ln ((r (\ cos \ varphi + i \ sin \ varphi)) ^ {n}) \\ & = n \ ln (r (\ cos \ varphi + i \ sin \ varphi)) \\ & = \ {n (\ ln (r) + (\ varphi + k2 \ pi) i) \ | \ k \ in \ mathbb {Z} \} \\ & = \ {n \ ln (r) + n \ varphi i + nk2 \ pi i \ | \ k \ in \ mathbb {Z} \}. \ end {aligned}}}

Cuando n es un número entero, esto simplifica a la fórmula de De Moivre:

{\ displaystyle z ^ {n} = (r (\ cos \ varphi + i \ sen \ varphi)) ^ {n} = r ^ {n} \ cdot (\ cos n \ varphi + i \ sen n \ varphi) .}

Las raíces

n

de

z

están dadas por

{\ sqrt [{n}] {z}} = {\ sqrt [{n}] {r}} \ left (\ cos \ left ({\ frac {\ varphi + 2k \ pi} {n}} \ right ) + i \ sin \ left ({\ frac {\ varphi + 2k \ pi} {n}} \ right) \ right)

para cualquier entero

k que

satisfaga

0 \leq k \leq n - 1

. Aquí n √ r es el habitual (positivo)

n

raíz ª del número real positivo

r

. Mientras que el

n

º raíz de un número real positivo

r

se elige para ser el positivo número real

c

satisfacer

c = r

no hay manera natural de distinguir un complejo particular,

n

º raíz de un número complejo. Por lo tanto, la raíz

n

de

z

se considera una función multivaluada (en

z

), a diferencia de una función usual

f

, para la cual

f (z)

es un número único definido. Fórmulas tales como

{\ sqrt [{n}] {z ^ {n}}} = z

(que es válido para números reales positivos), en general no es válido para números complejos.

Propiedades

Estructura de campo

El conjunto C de números complejos es un campo. Brevemente, esto significa que los siguientes hechos son válidos: primero, se pueden agregar y multiplicar dos números complejos para obtener otro número complejo. En segundo lugar, para cualquier número complejo

z

, su inversa aditiva

- z

también es un número complejo; y tercero, cada número complejo distinto de cero tiene un número complejo recíproco. Además, estas operaciones satisfacen una serie de leyes, por ejemplo, la ley de conmutatividad de suma y multiplicación para cualesquiera dos números complejos

z 1

y

z 2

:

z_ {1} + z_ {2} = z_ {2} + z_ {1},

z_ {1} z_ {2} = z_ {2} z_ {1}.

Estas dos leyes y los otros requisitos en un campo pueden ser probados por las fórmulas dadas anteriormente, usando el hecho de que los números reales forman un campo.

A diferencia de los reales, C no es un campo ordenado, es decir, no es posible definir una relación

z 1 < z 2

que sea compatible con la suma y la multiplicación. De hecho, en cualquier campo ordenado, el cuadrado de cualquier elemento es necesariamente positiva, por lo que

i = -1

opone a la existencia de un ordenamiento en C .

Cuando el campo subyacente de un tema o construcción matemática es el campo de números complejos, el nombre del tema generalmente se modifica para reflejar ese hecho. Por ejemplo: análisis complejo, matriz compleja, polinomio complejo y álgebra de Lie compleja.

Soluciones de ecuaciones polinómicas

Dado cualquier número complejo (llamado coeficientes)

a 0, ..., a n

, la ecuación

a_ {n} z ^ {n} + \ dotsb + a_ {1} z + a_ {0} = 0

tiene al menos una solución compleja z , siempre que al menos uno de los coeficientes más altos

a 1, ..., a n

no sea nulo. Esta es la afirmación del teorema fundamental del álgebra , de Carl Friedrich Gauss y Jean le Rond d'Alembert. Debido a este hecho, C se denomina campo algebraicamente cerrado. Esta propiedad no es válida para el campo de los números racionales Q (el polinomio

x - 2

no tiene una raíz racional, ya que
√
2 no es un número racional) ni los números reales R (el polinomio

x + a

no tiene una raíz real para

a > 0

, ya que el cuadrado de

x

es positivo para cualquier número real

x

).

Hay varias pruebas de este teorema, ya sea por métodos analíticos como el teorema de Liouville, o topológicos como el número de cuerda, o una prueba que combina la teoría de Galois y el hecho de que cualquier polinomio real de grado impar tiene al menos una raíz real.

Debido a este hecho, los teoremas que mantienen para cualquier campo algebraico cerrado , se aplican a C . Por ejemplo, cualquier matriz cuadrada compleja no vacía tiene al menos un valor propio (complejo).

Caracterización algebraica

El campo C tiene las siguientes tres propiedades: primero, tiene la característica 0. Esto significa que

1 + 1 + \dots + 1 \neq 0

para cualquier cantidad de sumandos (todos los cuales equivalen a uno). Segundo, su grado de trascendencia sobre Q , el campo principal de C , es la cardinalidad del continuo. En tercer lugar, está algebraicamente cerrado (ver arriba). Se puede demostrar que cualquier campo que tiene estas propiedades es isomorfo (como un campo) para C . Por ejemplo, el cierre algebraica de Q
p también satisface estas tres propiedades, por lo que estos dos campos son isomorfos (como campos, pero no como campos topológicas). Además, C es isomorfo al campo de la serie compleja Puiseux. Sin embargo, especificar un isomorfismo requiere el axioma de elección. Otra consecuencia de esta caracterización algebraica es que C contiene muchos subcampos adecuados que son isomorfo a C .

Caracterización como campo topológico

La caracterización anterior de C describe sólo los aspectos algebraicas de C . Es decir, las propiedades de proximidad y continuidad, que importan en áreas como el análisis y la topología, no se tratan. La siguiente descripción de C como un campo topológico (es decir, un campo que está equipado con una topología, que permite la noción de convergencia) tiene en cuenta las propiedades topológicas. C contiene un subconjunto

P

(es decir, el conjunto de números reales positivos) de elementos distintos de cero que cumplen las tres condiciones siguientes:

$P$ se cierra bajo suma, multiplicación y tomando inversas.
Si $x$ y $y$ son elementos distintos de $P$ , entonces o bien $x - y$ o $y - x$ está en $P$ .
Si $S$ es cualquier subconjunto no vacío de $P$ , entonces $S + P = x + P$ para algunos $x$ en C .

Por otra parte, C tiene un automorfismo involutivo no trivial

x \mapsto x *

(es decir, la conjugación compleja), tal que

x x *

es en

P

para cualquier distintos de cero

x

en C .

Cualquier campo

F

con estas propiedades puede dotarse de una topología tomando los conjuntos

B (x, p) = {y | p - (y - x) (y - x) * \in P}

como base, donde

x

oscila sobre el campo y

p

rangos de más de

P

. Con esta topología

F

es isomorfo como topológico campo para C .

Los campos topológicos localmente compactos solamente conectados son R y C . Esto proporciona otra caracterización de C como campo topológico, ya que C se puede distinguir de R porque los números complejos distintos de cero están conectados, mientras que los números reales distintos de cero no lo son.

Construcción formal

Construcción como pares ordenados

El conjunto

C

de números complejos se puede definir como el conjunto

R

de pares ordenados

(a, b)

de números reales, en el que se imponen las siguientes reglas para la suma y la multiplicación:

{\ begin {aligned} (a, b) + (c, d) & = (a + c, b + d) \\ (a, b) \ cdot (c, d) & = (ac-bd, bc + anuncio). \ end {aligned}}

Es solo una cuestión de notación expresar

(a, b)

como

a + bi

.

La construcción como campo de cociente

Aunque esta construcción de bajo nivel describe con precisión la estructura de los números complejos, la siguiente definición equivalente revela la naturaleza algebraica de

C

más inmediatamente. Esta caracterización se basa en la noción de campos y polinomios. Un campo es un conjunto dotado de operaciones de suma, resta, multiplicación y división que se comportan como es familiar a partir de, digamos, números racionales. Por ejemplo, la ley distributiva

(x + y) z = xz + yz

debe contener para cualquier tres elementos

x

,

y

y

z

de un campo. El conjunto

R

de números reales forma un campo. Un polinomio

p (X)

con coeficientes reales es una expresión de la forma

a_ {n} X ^ {n} + \ dotsb + a_ {1} X + a_ {0}

,

donde

a 0, ..., a n

son números reales. La adición y multiplicación habitual de polinomios dota al conjunto

R [X

de todos esos polinomios con una estructura de anillo. Este anillo se llama anillo polinomial sobre los números reales.

El conjunto de números complejos se define como el anillo del cociente

R [X] / (X + 1)

. Este campo de extensión contiene dos raíces cuadradas de

-1

, es decir (los conjuntos de)

X

y

- X

, respectivamente. (Las cosets de)

1

y

X

forman una base de

R [X] / (X + 1)

como un espacio vectorial real, lo que significa que cada elemento del campo de extensión puede escribirse de manera única como una combinación lineal en estos dos elementos. De forma equivalente, los elementos del campo de extensión pueden escribirse como pares ordenados

(a, b)

de números reales. El anillo del cociente es un campo, porque el

(X + 1)

es un ideal primordial en

R [X

, un dominio ideal principal, y por lo tanto es un ideal máximo.

Las fórmulas para la suma y la multiplicación en el anillo

R [X

, módulo la relación

(X = 1

corresponden a las fórmulas de suma y multiplicación de números complejos definidos como pares ordenados. Entonces las dos definiciones del campo

C

son isomórficas (como campos) .

Aceptando que

C

es algebraicamente cerrado, ya que es una extensión algebraica de

R

en este enfoque,

C

es por lo tanto el cierre algebraica de

R

.

Representación matricial de números complejos

Los números complejos

a + bi

también se pueden representar mediante matrices

2 \times 2

que tienen la siguiente forma:

{\ displaystyle {\ begin {pmatrix} a & -b \\ b & \; \; a \ end {pmatrix}}}

Aquí las entradas

a

y

b

son números reales. La suma y el producto de dos de tales matrices es nuevamente de esta forma, y la suma y el producto de los números complejos corresponde a la suma y el producto de tales matrices, siendo el producto:

{\ displaystyle {\ begin {pmatrix} a & -b \\ b & \; \; a \ end {pmatrix}} {\ begin {pmatrix} c & -d \\ d & \; \; c \ end {pmatrix}} = {\ begin {pmatrix} ac-bd & -ad-bc \\ bc + ad & \; \; - bd + ac \ end {pmatrix}}}

La descripción geométrica de la multiplicación de números complejos también puede expresarse en términos de matrices de rotación utilizando esta correspondencia entre números complejos y tales matrices. Además, el cuadrado del valor absoluto de un número complejo expresado como una matriz es igual al determinante de esa matriz:

{\ displaystyle | z | ^ {2} = {\ begin {vmatrix} a & -b \\ b & a \ end {vmatrix}} = a ^ {2} + b ^ {2}.}

El conjugado corresponde a la transposición de la matriz.

{\ overline {z}}

Aunque esta representación de números complejos con matrices es la más común, muchas otras representaciones surgen de matrices que no sean cuadradas a negativas de la matriz de identidad. Vea el artículo sobre 2 × 2 matrices reales para otras representaciones de números complejos.

{\ bigl (} {\ begin {smallmatrix} 0 & -1 \\ 1 & 0 \ end {smallmatrix}} {\ bigr)}

Análisis complejo

Gráfico de rueda de color de

sin (1 / z)

. Las partes negras en el interior se refieren a números que tienen grandes valores absolutos.

El estudio de las funciones de una variable compleja se conoce como análisis complejo y tiene un enorme uso práctico en las matemáticas aplicadas, así como en otras ramas de las matemáticas. A menudo, las pruebas más naturales para las declaraciones en el análisis real o incluso la teoría de los números emplean técnicas de análisis complejo (véase el teorema del número primo para un ejemplo). A diferencia de las funciones reales, que comúnmente se representan como gráficos bidimensionales, las funciones complejas tienen gráficos cuatridimensionales y pueden ilustrarse útilmente mediante la codificación por colores de un gráfico tridimensional para sugerir cuatro dimensiones, o animando la transformación dinámica de la función compleja del avión complejo.

Funciones exponenciales complejas y relacionadas

Las nociones de series convergentes y funciones continuas en el análisis (real) tienen análogos naturales en el análisis complejo. Se dice que una secuencia de números complejos converge si y solo si sus partes real e imaginaria lo hacen. Esto es equivalente a la definición (ε, δ) de límites, donde el valor absoluto de los números reales se reemplaza por el de los números complejos. Desde un punto de vista más abstracto, C , dotado de la métrica

{\ displaystyle \ operatorname {d} (z_ {1}, z_ {2}) = | z_ {1} -z_ {2} |}

es un espacio métrico completo, que incluye notablemente la desigualdad del triángulo

| z_ {1} + z_ {2} | \ leq | z_ {1} | + | z_ {2} |

para cualquier par de números complejos

z 1

y

z 2

.

Al igual que en el análisis real, esta noción de convergencia se utiliza para construir una serie de funciones elementales: la función exponencial

exp (z)

, también escrita

e

, se define como la serie infinita.

{\ displaystyle \ exp (z): = 1 + z + {\ frac {z ^ {2}} {2 \ cdot 1}} + {\ frac {z ^ {3}} {3 \ cdot 2 \ cdot 1} } + \ cdots = \ sum _ {n = 0} ^ {\ infty} {\ frac {z ^ {n}} {n!}}}}}

La serie que define las funciones trigonométricas reales seno y coseno, así como las funciones hiperbólicas sinh y cosh, también se transfieren a argumentos complejos sin cambios. Para las otras funciones trigonométricas e hiperbólicas, como la tangente, las cosas son un poco más complicadas, ya que las series definitorias no convergen para todos los valores complejos. Por lo tanto, uno debe definirlos en términos de seno, coseno y exponencial, o, de manera equivalente, utilizando el método de continuación analítica.

La fórmula de Euler dice:

{\ displaystyle \ exp (i \ varphi) = \ cos (\ varphi) + i \ sin (\ varphi)}

para cualquier número real φ , en particular

{\ displaystyle \ exp (i \ pi) = - 1}

A diferencia de la situación de los números reales, hay una infinitud de soluciones complejas

z

de la ecuación

{\ displaystyle \ exp (z) = w}

para cualquier número complejo

w \neq 0

. Se puede demostrar que cualquier solución

z

-llamada logaritmo complejo de

w

-satisface

{\ displaystyle \ log (w) = \ ln | w | + i \ arg (w),}

donde arg es el argumento definido anteriormente, y en el logaritmo natural (real). Como arg es una función multivaluada, única solo hasta un múltiplo de 2 π , log también tiene varios valores . El valor principal del registro a menudo se toma al restringir la parte imaginaria al intervalo

(-π, π)

.

La exponenciación compleja

z

se define como

{\ displaystyle z ^ {\ omega} = \ exp (\ omega \ log z),}

y tiene múltiples valores, excepto cuando es un número entero. Para

ω

= 1 /

n

, para un número natural

n

, esto recupera la no singularidad de

n las

raíces mencionadas anteriormente.

\omega

Los números complejos, a diferencia de los números reales, en general no satisfacen las identidades de poder y logaritmo no modificadas, particularmente cuando se tratan ingenuamente como funciones de un solo valor; ver falla de las identidades de poder y logaritmo. Por ejemplo, no satisfacen

{\ displaystyle a ^ {bc} = (a ^ {b}) ^ {c}.}

Ambos lados de la ecuación están multivariados por la definición de exponenciación compleja dada aquí, y los valores de la izquierda son un subconjunto de los de la derecha.

Funciones Holomorphic

Una función f : C → C se llama holomórfica si satisface las ecuaciones de Cauchy-Riemann. Por ejemplo, cualquier mapa R lineal C → C se puede escribir en la forma

f (z) = az + b {\ overline {z}}

con coeficientes complejos

a

y

b

. Este mapa es holomorfo si y solo si

b = 0

. El segundo summand es real-differentiable, pero no satisface las ecuaciones de Cauchy-Riemann.

b {\ overline {z}}

El análisis complejo muestra algunas características no aparentes en el análisis real. Por ejemplo, cualquiera de las dos funciones holomorfas

f

y

g

que están de acuerdo en una arbitrariamente pequeño subconjunto abierto de C necesariamente están de acuerdo en todas partes. Las funciones meromórficas, funciones que pueden escribirse localmente como

f (z) / (z - z 0)

con una función holomórfica

f

, aún comparten algunas de las características de las funciones holomórficas. Otras funciones tienen singularidades esenciales, como

sin (1 / z)

en

z = 0

.

Aplicaciones

Los números complejos tienen aplicaciones concretas esenciales en una variedad de áreas científicas y relacionadas, tales como procesamiento de señales, teoría de control, electromagnetismo, dinámica de fluidos, mecánica cuántica, cartografía y análisis de vibración. Algunas aplicaciones de números complejos son:

Teoría de control

En la teoría de control, los sistemas se transforman a menudo del dominio de tiempo al dominio de frecuencia usando la transformada de Laplace. Los ceros y polos del sistema se analizan luego en el plano complejo . El locus de la raíz, la trama de Nyquist y las técnicas de la trama de Nichols hacen uso del plano complejo.

En el método de locus de raíz, es importante si los ceros y los polos están en los semiplanos izquierdo o derecho, es decir, tienen una parte real mayor que o menor que cero. Si un sistema lineal, invariante en el tiempo (LTI) tiene polos que son

en el medio plano derecho, será inestable,
todo en el medio plano izquierdo, será estable,
en el eje imaginario, tendrá estabilidad marginal.

Si un sistema tiene ceros en el semiplano derecho, es un sistema de fase no mínimo.

Integrales impropias

En los campos aplicados, los números complejos se utilizan a menudo para calcular ciertas integrales impropias de valores reales, mediante funciones de valores complejos. Existen varios métodos para hacer esto; ver métodos de integración de contornos.

Dinámica de fluidos

En la dinámica de fluidos, las funciones complejas se utilizan para describir el flujo potencial en dos dimensiones.

Ecuaciones dinámicas

En ecuaciones diferenciales, es común encontrar primero todas las raíces complejas

r

de la ecuación característica de una ecuación diferencial lineal o sistema de ecuaciones y luego intentar resolver el sistema en términos de funciones base de la forma

f (t) = e

. Asimismo, en ecuaciones de diferencia, se usan las raíces complejas

r

de la ecuación característica del sistema de ecuación de diferencia, para intentar resolver el sistema en términos de funciones base de la forma

f (t) = r

.

Electromagnetismo e ingeniería eléctrica

En ingeniería eléctrica, la transformada de Fourier se usa para analizar voltajes y corrientes variables. El tratamiento de las resistencias, condensadores e inductores se puede unificar introduciendo resistencias imaginarias dependientes de la frecuencia para los dos últimos y combinando los tres en un único número complejo llamado impedancia. Este enfoque se llama cálculo fasorial.

En ingeniería eléctrica, la unidad imaginaria se denota por

j

, para evitar confusiones con

I

, que generalmente se usa para denotar una corriente eléctrica o, más particularmente,

i

, que generalmente se usa para denotar una corriente eléctrica instantánea.

Dado que la tensión en un circuito de CA está oscilando, se puede representar como

V (t) = V_ {0} e ^ {j \ omega t} = V_ {0} \ left (\ cos \ omega t + j \ sin \ omega t \ derecha),

Para obtener la cantidad medible, se toma la parte real:

v (t) = \ mathrm {Re} (V) = \ mathrm {Re} \ left [V_ {0} e ^ {j \ omega t} \ right] = V_ {0} \ cos \ omega t.

La señal de valor complejo se denomina representación analítica de la señal medible de valor real .

Vermont)

Vermont)

Análisis de señal

Los números complejos se utilizan en el análisis de señal y otros campos para una descripción conveniente para señales que varían periódicamente. Para funciones reales dadas que representan cantidades físicas reales, a menudo en términos de senos y cosenos, se consideran las funciones complejas correspondientes de las cuales las partes reales son las cantidades originales. Para una onda sinusoidal de una frecuencia dada, el valor absoluto

| z |

de la

z

correspondiente es la amplitud y el argumento

arg (z)

es la fase.

Si se emplea el análisis de Fourier para escribir una señal dada de valor real como una suma de funciones periódicas, estas funciones periódicas a menudo se escriben como funciones de valor complejo de la forma

{\ displaystyle x (t) = \ operatorname {Re} \ {X (t) \}}

y

{\ displaystyle X (t) = Ae ^ {i \ omega t} = ae ^ {i \ phi} e ^ {i \ omega t} = ae ^ {i (\ omega t + \ phi)}}

donde ω representa la frecuencia angular y el número complejo A codifica la fase y la amplitud como se explicó anteriormente.

Este uso también se extiende al procesamiento de señales digitales y procesamiento de imágenes digitales, que utilizan versiones digitales de análisis de Fourier (y análisis wavelet) para transmitir, comprimir, restaurar y procesar señales de audio digital, imágenes fijas y señales de video.

Otro ejemplo, relevante para las dos bandas laterales de modulación de amplitud de la radio AM, es:

{\ displaystyle {\ begin {aligned} \ cos ((\ omega + \ alpha) t) + \ cos \ left ((\ omega - \ alpha) t \ right) & = \ operatorname {Re} \ left (e ^ {i (\ omega + \ alpha) t} + e ^ {i (\ omega - \ alpha) t} \ right) \\ & = \ operatorname {Re} \ left ((e ^ {i \ alpha t} + e ^ {- i \ alpha t}) \ cdot e ^ {i \ omega t} \ right) \\ & = \ operatorname {Re} \ left (2 \ cos (\ alpha t) \ cdot e ^ {i \ omega t} \ right) \\ & = 2 \ cos (\ alpha t) \ cdot \ operatorname {Re} \ left (e ^ {i \ omega t} \ right) \\ & = 2 \ cos (\ alpha t ) \ cdot \ cos \ left (\ omega t \ right). \ end {aligned}}}

Mecánica cuántica

El campo de números complejos es intrínseco a las formulaciones matemáticas de la mecánica cuántica, donde los espacios complejos de Hilbert proporcionan el contexto para una de esas formulaciones que es conveniente y quizás la más estándar. Las fórmulas básicas originales de la mecánica cuántica, la ecuación de Schrödinger y la mecánica de la matriz de Heisenberg, hacen uso de números complejos.

Relatividad

En la relatividad especial y general, algunas fórmulas para la métrica del espacio-tiempo se vuelven más simples si se toma el componente de tiempo del continuo del espacio-tiempo para que sea imaginario. (Este enfoque ya no es estándar en la relatividad clásica, pero se usa de manera esencial en la teoría cuántica de campos). Los números complejos son esenciales para los espintores, que son una generalización de los tensores utilizados en la relatividad.

Geometría

Formas

Tres puntos no colineales en el plano determinan la forma del triángulo . Ubicando los puntos en el plano complejo, esta forma de un triángulo puede expresarse mediante aritmética compleja como

u, v, w

{\ displaystyle \ {u, v, w \}}

{\ displaystyle S (u, v, w) = {\ frac {uw} {uv}}.}

La forma de un triángulo seguirá siendo la misma, cuando el plano complejo se transforma por traslación o dilatación (mediante una transformación afín), que corresponde a la noción intuitiva de forma y describe la similitud. Por lo tanto, cada triángulo está en una clase de similitud de triángulos con la misma forma.

S

{\ displaystyle \ {u, v, w \}}

Fractales

Ciertos fractales se trazan en el plano complejo, por ejemplo, el conjunto de Mandelbrot y los conjuntos de Julia.

triangulos

Cada triángulo tiene una insólita de Steiner única: una elipse dentro del triángulo y tangente a los puntos medios de los tres lados del triángulo. Los focos de la inelíptica Steiner de un triángulo se pueden encontrar de la siguiente manera, de acuerdo con el teorema de Marden: Denomine los vértices del triángulo en el plano complejo como

a = x A + y A i

,

b = x B + y B i

, y

c = x C + y C i

. Escribe la ecuación cúbica

\ scriptstyle (xa) (xb) (xc) = 0

, tome su derivada e iguale la derivada (cuadrática) a cero. El teorema de Marden dice que las soluciones de esta ecuación son los números complejos que denotan las ubicaciones de los dos focos de la inellipse de Steiner.

Teoría de números algebraicos

Construcción de un pentágono regular con regla y brújula.

Como se mencionó anteriormente, cualquier ecuación polinómica no constante (en coeficientes complejos) tiene una solución en C . A fortiori, lo mismo es cierto si la ecuación tiene coeficientes racionales. Las raíces de tales ecuaciones se llaman números algebraicos, son un objeto principal de estudio en la teoría de números algebraicos. En comparación con Q , el cierre algebraico de Q , que también contiene todos los números algebraicos, C tiene la ventaja de ser fácilmente comprensible en términos geométricos. De esta manera, los métodos algebraicos se pueden utilizar para estudiar preguntas geométricas y viceversa. Con los métodos algebraicos, aplicando más específicamente la maquinaria de la teoría de campos al campo numérico que contiene las raíces de la unidad, se puede demostrar que no es posible construir un nonágono regular utilizando solo brújula y regla, un problema puramente geométrico.

Otro ejemplo son enteros de Gauss, es decir, números de la forma

x + iy

, donde

x

y

y

son números enteros, que se puede utilizar para clasificar las sumas de cuadrados.

Teoría analítica de números

La teoría de números analíticos estudia números, a menudo enteros o racionales, aprovechando el hecho de que pueden considerarse como números complejos, en los que se pueden usar métodos analíticos. Esto se hace codificando la información teórica de números en funciones de valores complejos. Por ejemplo, la función

R (s) de

Riemann se relaciona con la distribución de los números primos.

Historia

La referencia efímera más temprana a raíces cuadradas de números negativos puede quizás decirse que ocurre en la obra del matemático griego Héroe de Alejandría en el siglo I dC, donde en su Stereometrica considera, aparentemente erróneamente, el volumen de un tronco trunco imposible. una pirámide para llegar al término en sus cálculos, aunque las cantidades negativas no se concibieron en las matemáticas helenísticas y Heron simplemente lo reemplazó por su positivo ( ).

\ scriptstyle {\ sqrt {81-144}} = 3i {\ sqrt {7}}

\ scriptstyle {\ sqrt {144-81}} = 3 {\ sqrt {7}}

El ímpetu por estudiar números complejos como un tema en sí mismo surgió por primera vez en el siglo XVI cuando los matemáticos italianos descubrieron soluciones algebraicas para las raíces de polinomios cúbicos y cuárticos (ver Niccolò Fontana Tartaglia, Gerolamo Cardano). Pronto se dio cuenta de que estas fórmulas, incluso si uno solo estaba interesado en soluciones reales, a veces requerían la manipulación de raíces cuadradas de números negativos. Como ejemplo, la fórmula de Tartaglia para una ecuación cúbica de la forma da la solución a la ecuación

x

=

x

como

\ scriptstyle x ^ {3} = px + q

{\ frac {1} {\ sqrt {3}}} \ left (({\ sqrt {-1}}) ^ {1/3} + {\ frac {1} {({\ sqrt {-1}} ) ^ {1/3}}} \ right).

A primera vista, esto parece una tontería. Sin embargo, los cálculos formales con números complejos muestran que la ecuación

z = i

tiene soluciones

- i

, y . Sustituyendo estos a su vez por la fórmula cúbica de Tartaglia y simplificando, uno obtiene 0, 1 y -1 como soluciones de

x

-

x

= 0

{\ scriptstyle {\ frac {\ sqrt {3}} {2}}} + {\ scriptstyle {\ frac {1} {2}}} i

{\ scriptstyle {\ frac {- {\ sqrt {3}}} {2}}} + {\ scriptstyle {\ frac {1} {2}}} i

{\ scriptstyle {\ sqrt {-1}} ^ {1/3}}

. Por supuesto, esta ecuación particular puede resolverse a primera vista, pero ilustra que cuando se usan fórmulas generales para resolver ecuaciones cúbicas con raíces reales, entonces, como los matemáticos posteriores mostraron rigurosamente, el uso de números complejos es inevitable. Rafael Bombelli fue el primero en abordar explícitamente estas soluciones aparentemente paradójicas de ecuaciones cúbicas y desarrolló las reglas para la aritmética compleja al tratar de resolver estos problemas.

El término "imaginario" para estas cantidades fue acuñado por René Descartes en 1637, aunque se esforzó por enfatizar su naturaleza imaginaria.

[...] a veces solo imaginario, es decir uno puede imaginar tantos como dije en cada ecuación, pero a veces no existe una cantidad que coincida con lo que imaginamos.
([...] quelquefois seulement imaginaires c'est-à-dire que l'on peut toujours en imaginer autant que j'ai dit en chaque équation, mais qu'il n'y a quelquefois aucune quantité qui corresponde à celle qu 'en imaginar.)

Otra fuente de confusión fue que la ecuación parecía ser categóricamente inconsistente con la identidad algebraica , que es válida para números reales no negativos

a

y

b

, y que también se usó en cálculos de números complejos con uno de

a

,

b

positivo y el otro negativo El uso incorrecto de esta identidad (y la identidad relacionada ) en el caso en que tanto

a

como

b

son negativos, incluso entorpece a Euler. Esta dificultad finalmente llevó a la convención de usar el símbolo especial

i

en lugar de √ -1

\ scriptstyle {\ sqrt {-1}} ^ {2} = {\ sqrt {-1}} {\ sqrt {-1}} = - 1

\ scriptstyle {\ sqrt {a}} {\ sqrt {b}} = {\ sqrt {ab}}

\ scriptstyle {\ frac {1} {\ sqrt {a}}} = {\ sqrt {\ frac {1} {a}}}

para evitar este error. Aun así, Euler consideró natural introducir a los estudiantes a números complejos mucho antes de lo que lo hacemos hoy. En su libro de texto de álgebra elemental, Elements of Algebra, introduce estos números casi a la vez y luego los utiliza de forma natural en todo.

En el siglo XVIII, los números complejos ganaron un uso más amplio, ya que se observó que la manipulación formal de expresiones complejas podía usarse para simplificar los cálculos que involucraban funciones trigonométricas. Por ejemplo, en 1730 Abraham de Moivre señaló que las identidades complicadas que relacionan las funciones trigonométricas de un múltiplo entero de un ángulo con las potencias de las funciones trigonométricas de ese ángulo podrían ser simplemente reexpresadas por la siguiente fórmula conocida que lleva su nombre, de La fórmula de Moivre:

{\ displaystyle (\ cos \ theta + i \ sin \ theta) ^ {n} = \ cos n \ theta + i \ sin n \ theta.}

En 1748 Leonhard Euler fue más allá y obtuvo la fórmula de Euler de análisis complejo:

{\ displaystyle \ cos \ theta + i \ sin \ theta = e ^ {i \ theta}}

al manipular formalmente series de poder complejas y observó que esta fórmula podría usarse para reducir cualquier identidad trigonométrica a identidades exponenciales mucho más simples.

La idea de un número complejo como un punto en el plano complejo (arriba) fue descrita por primera vez por Caspar Wessel en 1799, aunque se había anticipado ya en 1685 en el Tractatus De Algebra de Wallis .

Las memorias de Wessel aparecieron en los Procedimientos de la Academia de Copenhague, pero pasaron casi desapercibidas. En 1806, Jean-Robert Argand publicó de forma independiente un folleto sobre números complejos y proporcionó una prueba rigurosa del teorema fundamental del álgebra. Carl Friedrich Gauss había publicado anteriormente una prueba esencialmente topológica del teorema en 1797, pero expresó sus dudas en ese momento sobre "la verdadera metafísica de la raíz cuadrada de -1". No fue sino hasta 1831 que superó estas dudas y publicó su tratado sobre números complejos como puntos en el plano, estableciendo en gran parte la notación y la terminología modernas. A principios del siglo XIX, otros matemáticos descubrieron independientemente la representación geométrica de los números complejos: Buée, Mourey, Warren, Français y su hermano, Bellavitis.

El matemático inglés GH Hardy comentó que Gauss fue el primer matemático en usar números complejos de "una manera realmente segura y científica" aunque matemáticos como Niels Henrik Abel y Carl Gustav Jacob Jacobi necesariamente los usaban rutinariamente antes de que Gauss publicara su tratado de 1831. Augustin Louis Cauchy y Bernhard Riemann juntos llevaron las ideas fundamentales del análisis complejo a un alto nivel de cumplimiento, comenzando alrededor de 1825 en el caso de Cauchy.

Los términos comunes utilizados en la teoría se deben principalmente a los fundadores. Argand llamó el factor de dirección y el módulo ; Cauchy (1828) llamó a la forma reducida (l'expression réduite) y aparentemente introdujo el término argumento ; Gauss usó

i

for , introdujo el término número complejo para

a

+

bi

y llamó

a

+

b

la norma . El coeficiente de dirección de expresión , a menudo utilizado para , se debe a Hankel (1867) y al valor absoluto, para

\ scriptstyle \ cos \ phi + i \ sin \ phi

\ scriptstyle r = {\ sqrt {a ^ {2} + b ^ {2}}}

\ cos \ phi + i \ sin \ phi

\ scriptstyle {\ sqrt {-1}}

\ cos \ phi + i \ sin \ phi

módulo, se debe a Weierstrass.

Escritores clásicos posteriores sobre la teoría general incluyen Richard Dedekind, Otto Hölder, Felix Klein, Henri Poincaré, Hermann Schwarz, Karl Weierstrass y muchos otros.

Generalizaciones y nociones relacionadas

El proceso de extender el campo R de reales a C se conoce como la construcción de Cayley-Dickson. Se puede llevar más lejos a dimensiones más altas, produciendo los cuaterniones H y octoniones O que (como un espacio vectorial real) son de dimensión 4 y 8, respectivamente. En este contexto, los números complejos se han llamado binarios .

Del mismo modo que al aplicar la construcción a los valores reales, se pierde la propiedad de ordenar, las propiedades familiares de los números reales y complejos se desvanecen con cada extensión. Los cuaterniones pierden conmutatividad, es decir:

x • y \neq y • x

para algunos cuaterniones

x, y,

y la multiplicación de octoniones, además de no ser conmutativa, no es asociativa:

(x • y) • z \neq x • (y • z)

para algunos octonions

x, y, z .

Reals, números complejos, los cuaterniones y octoniones están normadas álgebra de división sobre R . Según el teorema de Hurwitz, son los únicos; las sedenions, el siguiente paso en la construcción de Cayley-Dickson, no tienen esta estructura.

La construcción de Cayley-Dickson está estrechamente relacionada con la representación regular de C , considerada como un R- álgebra (un espacio de R- vector con una multiplicación), con respecto a la base

(1, i)

. Esto significa lo siguiente: el mapa lineal R

\ mathbb {C} \ rightarrow \ mathbb {C}, z \ mapsto wz

para un número complejo fijo,

w

puede representarse con una matriz de

2 \times 2

(una vez que se ha elegido una base). Con respecto a la base

(1, i)

, esta matriz es

{\ begin {pmatrix} \ operatorname {Re} (w) & - \ operatorname {Im} (w) \\\ operatorname {Im} (w) & \; \; \ operatorname {Re} (w) \ end { pmatrix}}

es decir, el mencionado en la sección sobre la representación matricial de los números complejos anteriores. Si bien esta es una representación lineal de C en las matrices reales de 2 × 2, no es la única. Cualquier matriz

J = {\ begin {pmatrix} p & q \\ r & -p \ end {pmatrix}}, \ quad p ^ {2} + qr + 1 = 0

tiene la propiedad de que su cuadrado es el negativo de la matriz de identidad:

J = - I

. Entonces

{\ displaystyle \ {z = aI + bJ: a, b \ in \ mathbf {R} \}}

También es isomorfo al campo C , y da una compleja estructura alternativa en R . Esto se generaliza por la noción de una estructura compleja lineal.

Números hipercomplejos también generalizan R , C , H , y O . Por ejemplo, esta noción contiene los números del complejo dividido, que son elementos del anillo

R [x] / (x - 1)

(en oposición a

R [x] / (x + 1)

). En este anillo, la ecuación

a = 1

tiene cuatro soluciones.

El campo R es la terminación de Q , el campo de los números racionales, con respecto a la métrica de valor absoluto habitual. Otras opciones de métricas de Q conducen a los campos Q p de pnúmeros -adic (para cualquier número primo p ), que son de ese modo análogo a R . No hay otras formas no triviales de completar Q que R y Q p , según el teorema de Ostrowski. Los cierres algebraicos de Q p todavía tienen una norma, pero (a diferencia de C ) no están completos con respecto a ella. La finalización de

{\ overline {\ mathbf {Q} _ {p}}}

\ mathbf {C} _ {p}

{\ overline {\ mathbf {Q} _ {p}}}

resulta ser algebraicamente cerrado. Este campo se llama números complejos p -adic por analogía.

Los campos R y Q p y sus extensiones de campo finito, incluido C , son campos locales.

Buscar en este blog

Wikiblog Cultulandia [es]

Número complejo

Número complejo

Definición

Visión de conjunto

Definición

Forma cartesiana y definición a través de pares ordenados

Plano complejo

Historia en breve

Notación

Relaciones de igualdad y orden

Operaciones elementales

Conjugado

Adición y sustracción

Multiplicación y división

Recíproco

Raíz cuadrada

Forma polar

Valor y argumento absolutos

Multiplicación y división en forma polar

Exponenciación

Fórmula de Euler

Logaritmo natural

Exponentes enteros y fraccionarios

Propiedades

Estructura de campo

Soluciones de ecuaciones polinómicas

Caracterización algebraica

Caracterización como campo topológico

Construcción formal

Construcción como pares ordenados

La construcción como campo de cociente

Representación matricial de números complejos

Análisis complejo

Funciones exponenciales complejas y relacionadas

Funciones Holomorphic

Aplicaciones

Teoría de control

Integrales impropias

Dinámica de fluidos

Ecuaciones dinámicas

Electromagnetismo e ingeniería eléctrica

Análisis de señal

Mecánica cuántica

Relatividad

Geometría

Formas

Fractales

triangulos

Teoría de números algebraicos

Teoría analítica de números

Historia

Generalizaciones y nociones relacionadas

Contenidos Relacionados de Matemáticas ››