Wikiblog Cultulandia [es]

Un número entero (del entero latino que significa "entero") es un número que se puede escribir sin un componente fraccionario. Por ejemplo, 21, 4, 0 y -2048 son números enteros, mientras que 9,75, 5 1/2 , y

\sqrt 2

no lo son.

El conjunto de números enteros consiste en cero (0), los números naturales positivos (1, 2, 3, ...), también llamados números enteros o números de conteo , y sus inversas aditivas (los enteros negativos , es decir, -1, -2, -3, ...). El conjunto de enteros a menudo se denota con una negrita Z ("

Z

") o negrita en la pizarra (Unicode U + 2124 ℤ) representando la palabra alemana Zahlen (

\ mathbb {Z}

[Tsaːlən] , "números").

Z

es un subconjunto del conjunto de todos los números racionales

Q

, a su vez, un subconjunto de los números reales

R

. Al igual que los números naturales,

Z

es contablemente infinito.

Los enteros forman el grupo más pequeño y el anillo más pequeño que contiene los números naturales. En la teoría de números algebraicos, los enteros a veces se califican como enteros racionales para distinguirlos de los enteros algebraicos más generales. De hecho, los enteros (racionales) son los enteros algebraicos que también son números racionales.

Símbolo

El símbolo

Z

puede anotarse para denotar varios conjuntos, con uso variable entre diferentes autores:

Z

,

Z +

o

Z

para los enteros positivos,

Z

para enteros no negativos,

Z

para enteros distintos de cero. Algunos autores usan

Z

para enteros distintos de cero, otros lo usan para enteros no negativos, o para

{-1, 1}

. Además,

Z p

se usa para denotar el conjunto de enteros módulo

p

, es decir, un conjunto de clases de congruencia de enteros, o el conjunto de enteros

p

-adic.

Propiedades algebraicas

Los números enteros se pueden considerar puntos discretos e igualmente espaciados en una recta numérica infinitamente larga. En lo anterior, los enteros no negativos se muestran en números enteros morados y negativos en rojo.

Al igual que los números naturales,

Z

se cierra bajo las operaciones de suma y multiplicación, es decir, la suma y el producto de dos enteros es un número entero. Sin embargo, con la inclusión de los números naturales negativos, y, lo que es más importante, 0,

Z

(a diferencia de los números naturales) también se cierra por sustracción. Los enteros forman un anillo unitario que es el más básico, en el siguiente sentido: para cualquier anillo unitario, hay un único homomorfismo de anillo de los enteros en este anillo. Esta propiedad universal, a saber, ser un objeto inicial en la categoría de anillos, que caracteriza el anillo

Z

.

Z

no está cerrado por división, ya que el cociente de dos enteros (p. Ej., 1 dividido por 2) no necesita ser un número entero. Aunque los números naturales se cierran bajo exponenciación, los enteros no (dado que el resultado puede ser una fracción cuando el exponente es negativo).

A continuación se enumeran algunas de las propiedades básicas de la suma y la multiplicación para cualquier número entero

a

,

b

y

c

.

Propiedades de suma y multiplicación en enteros
	Adición	Multiplicación
Cierre:	$a + b$ es un número entero	$a \times b$ es un número entero
Asociatividad:	$a + (b + c) = (a + b) + c$	$a \times (b \times c) = (a \times b) \times c$
Conmutatividad	$a + b = b + a$	$a \times b = b \times a$
Existencia de un elemento de identidad:	$a + 0 = a$	$a \times 1 = a$
Existencia de elementos inversos:	$a + (- a) = 0$	Los únicos enteros racionales invertibles (unidades llamadas) son $-1$ y $1$ .
Distributividad:	$a \times (b + c) = (a \times b) + (a \times c)$ y $($ $a$ $+$ $b$ $) \times$ $c$ $= ($ $a$ $\times$ $c$ $) + ($ $b$ $\times$ $c$ $)$
Sin divisores cero		Si $a \times b = 0$ , entonces $a = 0$ o $b = 0$ (o ambos)

En el lenguaje del álgebra abstracta, las primeras cinco propiedades enumeradas anteriormente para la adición dicen que

Z

debajo de la suma es un grupo abeliano. También es un grupo cíclico, ya que cada entero distinto de cero se puede escribir como una suma finita 1 + 1 + ... + 1 o (-1) + (-1) + ... + (-1) . De hecho,

Z

bajo la adición es la única grupo cíclico infinito, en el sentido de que cualquier grupo cíclico infinito es isomorfo a

Z

.

Las primeras cuatro propiedades enumeradas anteriormente para la multiplicación dicen que

Z

bajo la multiplicación es un monoide conmutativo. Sin embargo, no todos los números tienen una inversa multiplicativa; por ejemplo, no hay un número entero

x

tal que

2 x = 1,

porque el lado izquierdo es par, mientras que el lado derecho es impar. Esto significa que

Z

bajo la multiplicación no es un grupo.

Todas las reglas de la tabla de propiedades anterior, excepto la última, tomadas juntas dicen que

Z

junto con la suma y la multiplicación es un anillo conmutativo con unidad. Es el prototipo de todos los objetos de dicha estructura algebraica. Solo esas igualdades de expresiones son verdaderas en

Z

para todos los valores de variables, que son verdaderas en cualquier anillo conmutativo unital. Tenga en cuenta que ciertos enteros distintos de cero se asignan a cero en ciertos anillos.

La falta de divisores cero en los enteros (última propiedad en la tabla) significa que el anillo conmutativo

Z

es un dominio integral.

La falta de inversas multiplicativas, que es equivalente al hecho de que

Z

no está cerrado por división, significa que

Z

no es un campo. El campo más pequeño que contiene los enteros como subring es el campo de los números racionales. El proceso de construcción de los racionales a partir de los enteros puede imitarse para formar el campo de fracciones de cualquier dominio integral. Y de regreso, comenzando desde un campo de número algebraico (una extensión de números racionales), se puede extraer su anillo de enteros, que incluye

Z

como subrrededor.

Aunque la división ordinaria no está definida en

Z

, la división "con resto" se define en ellas. Se llama división euclidiana y posee la siguiente propiedad importante: es decir, dados dos enteros

a

y

b

con

b \neq 0

, existen enteros únicos

q

y

r

tales que

a = q \times b + r

y

0 \leq r <| b |

, donde

| b |

denota el valor absoluto de

b

. El entero

q

se llama cociente y

r

se llama el resto de la división de

una

por

b

. El algoritmo euclidiano para calcular los mayores divisores comunes funciona mediante una secuencia de divisiones euclidianas.

De nuevo, en el lenguaje del álgebra abstracta, lo anterior dice que Z es un dominio euclidiano. Esto implica que

Z

es un dominio ideal principal y cualquier entero positivo se puede escribir como productos de primos de una manera esencialmente única. Este es el teorema fundamental de la aritmética.

Propiedades teóricas de orden

Z

es un conjunto totalmente ordenado sin límite superior o inferior. El orden de

Z

viene dado por::

... -3 <-2 <-1 <0 <1 <2 <3 <...

Un entero es positivo si es mayor que cero y negativo si es menor que cero. Cero se define como ni negativo ni positivo.

El orden de los enteros es compatible con las operaciones algebraicas de la siguiente manera:

si $a < b$ y $c < d$ , entonces $a + c < b + d$
si $a < b$ y $0 < c$ , entonces $ac < bc$ .

Se deduce que

Z

junto con el orden anterior es un anillo ordenado.

Los enteros son el único grupo abeliano no trivial totalmente ordenado cuyos elementos positivos están bien ordenados. Esto es equivalente a la afirmación de que cualquier anillo de valoración noetheriano es un campo o un anillo de valoración discreto.

Construcción

Los puntos rojos representan pares ordenados de números naturales. Los puntos rojos vinculados son clases de equivalencia que representan los enteros azules al final de la línea.

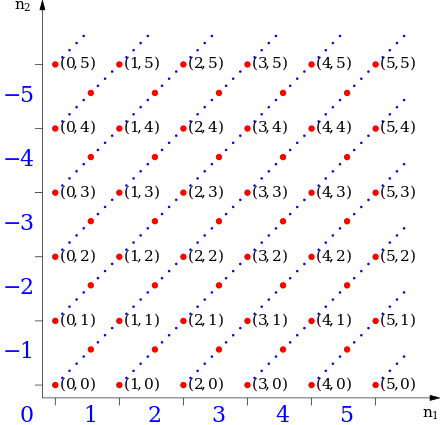
En la enseñanza primaria, los enteros a menudo se definen intuitivamente como los números naturales (positivos), cero y las negaciones de los números naturales. Sin embargo, este estilo de definición conduce a muchos casos diferentes (cada operación aritmética debe definirse en cada combinación de tipos de números enteros) y hace tedioso probar que estas operaciones obedecen a las leyes de la aritmética. Por lo tanto, en las matemáticas teóricas de conjuntos modernas, a menudo se usa una construcción más abstracta, que permite definir las operaciones aritméticas sin distinción de caso. Por lo tanto, los enteros pueden construirse formalmente como clases de equivalencia de pares ordenados de números naturales

(a, b)

.

La intuición es que

(a, b)

representa el resultado de restar

b

de

a

. Para confirmar nuestra expectativa de que 1 - 2 y 4 - 5 denotan el mismo número, definimos una relación de equivalencia

~

en estos pares con la siguiente regla:

{\ displaystyle (a, b) \ sim (c, d)}

precisamente cuando

{\ displaystyle a + d = b + c.}

La suma y multiplicación de enteros se puede definir en términos de operaciones equivalentes en los números naturales; que denota por

[(a, b)]

la clase de equivalencia que tiene

(a, b)

como miembro, uno tiene:

{\ displaystyle [(a, b)] + [(c, d)]: = [(a + c, b + d)].}

{\ displaystyle [(a, b)] \ cdot [(c, d)]: = [(ac + bd, ad + bc)].}

La negación (o inversión aditiva) de un entero se obtiene invirtiendo el orden del par:

{\ displaystyle - [(a, b)]: = [(b, a)].}

Por lo tanto, la resta se puede definir como la adición del inverso aditivo:

{\ displaystyle [(a, b)] - [(c, d)]: = [(a + d, b + c)].}

El orden estándar en los enteros viene dado por:

{\ displaystyle [(a, b)] <[(c, d)]}

iff

{\ displaystyle a + d <b + c.}

Se verifica fácilmente que estas definiciones son independientes de la elección de representantes de las clases de equivalencia.

Cada clase de equivalencia tiene un miembro único que tiene la forma

(n, 0)

o

(0, n)

(o ambos a la vez). El número natural

n

se identifica con la clase

[(n, 0)]

(en otras palabras, los números naturales se incrustan en los enteros mediante el envío de mapas

n

a

[(n, 0)]

), y la clase

[(0, n))]

se denota

- n

(esto cubre todas las clases restantes, y da la clase

[(0,0)]

una segunda vez desde

-0 = 0.

Por lo tanto,

[(a, b)]

se denota por

{\ begin {cases} ab, & {\ mbox {if}} a \ geq b \\ - (ba), & {\ mbox {if}} a <b. \ end {cases}}

Si los números naturales se identifican con los enteros correspondientes (utilizando la inserción mencionada anteriormente), esta convención no crea ambigüedad.

Esta notación recupera la representación familiar de los enteros como

{..., -2, -1, 0, 1, 2, ...

}.

Algunos ejemplos son:

{\ begin {aligned} 0 & = [(0,0)] & = [(1,1)] & = \ cdots && = [(k, k)] \\ 1 & = [(1,0)] & = [(2,1)] & = \ cdots && = [(k + 1, k)] \\ - 1 & = [(0,1)] & = [(1,2)] & = \ cdots && = [ (k, k + 1)] \\ 2 & = [(2,0)] & = [(3,1)] & = \ cdots && = [(k + 2, k)] \\ - 2 & = [( 0,2)] & = [(1,3)] & = \ cdots && = [(k, k + 2)]. \ End {aligned}}

En la informática teórica, otros enfoques para la construcción de enteros son utilizados por demostradores de teoremas automatizados y motores de reescritura de términos. Los enteros se representan como términos algebraicos construidos usando algunas operaciones básicas (como cero , succ , pred , etc.) y, posiblemente, usando números naturales, que se supone que ya están construidos (por ejemplo, usando el enfoque de Peano).

Existen al menos diez de tales construcciones de enteros con signo. Estas construcciones difieren de varias maneras: el número de operaciones básicas utilizadas para la construcción, el número (por lo general, entre 0 y 2) y los tipos de argumentos aceptados por estas operaciones; la presencia o ausencia de números naturales como argumentos de algunas de estas operaciones, y el hecho de que estas operaciones son constructores libres o no, es decir, que el mismo entero puede representarse utilizando solo uno o varios términos algebraicos.

La técnica para la construcción de enteros presentada anteriormente en esta sección corresponde al caso particular donde hay un único par de operaciones básicas que toma como argumentos dos números naturales y , y devuelve un número entero (igual a ). Esta operación no es gratuita ya que el número entero 0 puede escribirse par (0,0), o par (1,1), o par (2,2), etc. Esta técnica de construcción es utilizada por el asistente de pruebas Isabelle; sin embargo, muchas otras herramientas utilizan técnicas de construcción alternativas, destacando aquellas basadas en constructores libres, que son más simples y se pueden implementar de manera más eficiente en las computadoras.

(x, y)

X

y

xy

Ciencias de la Computación

Un entero es a menudo un tipo de datos primitivo en los lenguajes de computadora. Sin embargo, los tipos de datos enteros solo pueden representar un subconjunto de todos los enteros, ya que las computadoras prácticas son de capacidad finita. Además, en la representación complementaria de los dos comunes, la definición inherente de signo distingue entre "negativo" y "no negativo" en lugar de "negativo, positivo y 0". (Sin embargo, es ciertamente posible que una computadora determine si un valor entero es realmente positivo). Los tipos de datos de aproximación entera de longitud fija (o subconjuntos) se denotan int o Integer en varios lenguajes de programación (como Algol68, C, Java, Delphi, etc.).

Las representaciones de longitud variable de enteros, como bignums, pueden almacenar cualquier número entero que se ajuste a la memoria de la computadora. Otros tipos de datos enteros se implementan con un tamaño fijo, generalmente un número de bits que es una potencia de 2 (4, 8, 16, etc.) o un número memorable de dígitos decimales (por ejemplo, 9 o 10).

Cardinalidad

La cardinalidad del conjunto de enteros es igual a

ℵ 0

(aleph-null). Esto se demuestra fácilmente mediante la construcción de una biyección, es decir, una función que es inyectiva y sobreyectiva de

Z

a

N

. Si

N = {0, 1, 2, ...}

entonces considere la función:

f (x) = {\ begin {cases} 2 | x |, & {\ mbox {if}} x \ leq 0 \\ 2x-1, & {\ mbox {if}} x> 0. \ end {cases }}

{... (-4,8) (-3,6) (-2,4) (-1,2) (0,0) (1,1) (2,3) (3,5) ...}

Si

N = {1, 2, 3, ...}

entonces considere la función:

g (x) = {\ begin {cases} 2 | x |, & {\ mbox {if}} x <0 \\ 2x + 1, & {\ mbox {if}} x \ geq 0. \ end {cases }}

{... (-4,8) (-3,6) (-2,4) (-1,2) (0,1) (1,3) (2,5) (3,7) ...}

Si el dominio está restringido a

Z,

entonces cada miembro de

Z

tiene uno y solo un miembro correspondiente de N, y por la definición de igualdad cardinal, los dos conjuntos tienen la misma cardinalidad.

Buscar en este blog