Matemáticas
Definición
Matemáticas (del griego μάθημα máthēma , "conocimiento, estudio, aprendizaje") es el estudio de temas tales como cantidad, estructura, espacio y cambio. No tiene una definición generalmente aceptada.
Los matemáticos buscan y usan patrones para formular nuevas conjeturas; ellos resuelven la verdad o la falsedad de las conjeturas mediante una prueba matemática. Cuando las estructuras matemáticas son buenos modelos de fenómenos reales, el razonamiento matemático puede proporcionar información o predicciones sobre la naturaleza. Mediante el uso de la abstracción y la lógica, las matemáticas se desarrollaron a partir del conteo, el cálculo, la medición y el estudio sistemático de las formas y movimientos de los objetos físicos. Las matemáticas prácticas han sido una actividad humana desde la existencia de registros escritos. La investigación requerida para resolver problemas matemáticos puede llevar años o incluso siglos de indagaciones sostenidas.
Los argumentos rigurosos aparecieron por primera vez en las matemáticas griegas, sobre todo en los Elementos de Euclides . Desde el trabajo pionero de Giuseppe Peano (1858-1932), David Hilbert (1862-1943) y otros sobre sistemas axiomáticos a finales del siglo XIX, se ha convertido en costumbre considerar que la investigación matemática establece la verdad mediante la deducción rigurosa de los axiomas apropiadamente elegidos. y definiciones. Las matemáticas se desarrollaron a un ritmo relativamente lento hasta el Renacimiento, cuando las innovaciones matemáticas que interactúan con los nuevos descubrimientos científicos condujeron a un rápido aumento en la tasa de descubrimiento matemático que ha continuado hasta nuestros días.
Galileo Galilei (1564-1642) dijo: "El universo no se puede leer hasta que hayamos aprendido el idioma y nos hayamos familiarizado con los personajes en los que está escrito. Está escrito en lenguaje matemático, y las letras son triángulos, círculos y otras formas geométricas. figuras, sin lo cual significa que es humanamente imposible de comprender una sola palabra. Sin éstos, uno está deambulando en un oscuro laberinto ". Carl Friedrich Gauss (1777-1855) se refirió a las matemáticas como "la Reina de las Ciencias". Benjamin Peirce (1809-1880) llamó a las matemáticas "la ciencia que saca las conclusiones necesarias". David Hilbert dijo de las matemáticas: "No estamos hablando aquí de arbitrariedad en ningún sentido. Las matemáticas no son como un juego cuyas tareas están determinadas por reglas arbitrariamente estipuladas. es un sistema conceptual que posee una necesidad interna que solo puede serlo y de ninguna otra manera ". Albert Einstein (1879-1955) afirmó que" en la medida en que las leyes de las matemáticas se refieren a la realidad, no son ciertas; y en la medida en que están seguros, no se refieren a la realidad ".
Las matemáticas son esenciales en muchos campos, incluidas las ciencias naturales, la ingeniería, la medicina, las finanzas y las ciencias sociales. Las matemáticas aplicadas han llevado a disciplinas matemáticas completamente nuevas, como las estadísticas y la teoría de juegos. Los matemáticos se dedican a las matemáticas puras, o las matemáticas por sí mismas, sin tener ninguna aplicación en mente. Las aplicaciones prácticas para lo que comenzó como las matemáticas puras a menudo se descubren.
Historia
La historia de las matemáticas se puede ver como una serie de abstracciones cada vez mayor. La primera abstracción, compartida por muchos animales, fue probablemente la de los números: la constatación de que una colección de dos manzanas y una colección de dos naranjas (por ejemplo) tienen algo en común, a saber, la cantidad de sus miembros.
Como lo demuestran los recuentos encontrados en los huesos, además de reconocer cómo contar los objetos físicos, los pueblos prehistóricos también pueden haber reconocido cómo contar cantidades abstractas, como días, estaciones y años.
La evidencia de las matemáticas más complejas no aparece hasta alrededor de 3000 aC, cuando los babilonios y los egipcios comenzaron a utilizar la aritmética, el álgebra y la geometría para los impuestos y otros cálculos financieros, para la construcción y la construcción, y para la astronomía. Los usos más antiguos de las matemáticas fueron en el comercio, la medición de la tierra, la pintura y los patrones de tejido y el registro del tiempo.
En las matemáticas babilónicas, la aritmética elemental (suma, resta, multiplicación y división) aparece por primera vez en el registro arqueológico. Los sistemas numerales de escritura y numeración anteriores han sido muchos y diversos, con los primeros números escritos conocidos creados por egipcios en textos del Reino Medio como el Papiro Matemático Rhind.
Entre 600 y 300 aC, los antiguos griegos comenzaron un estudio sistemático de las matemáticas en sí mismas con las matemáticas griegas.
Durante la Edad de Oro del Islam, especialmente durante los siglos IX y X, las matemáticas vieron muchas innovaciones importantes basadas en las matemáticas griegas: la mayoría de ellas incluyen las contribuciones de los matemáticos persas como Al-Khwarismi, Omar Khayyam y Sharaf al-Dīn al-Ṭūsī .
Desde entonces, las matemáticas se han ampliado mucho, y ha habido una interacción fructífera entre las matemáticas y la ciencia, en beneficio de ambos. Los descubrimientos matemáticos se siguen haciendo hoy. Según Mikhail B. Sevryuk, en la edición de enero de 2006 del Boletín de la American Mathematical Society , "la cantidad de documentos y libros incluidos en la base de datos de Revisiones Matemáticas desde 1940 (el primer año de funcionamiento de MR) es ahora más de 1,9 millones y se agregan más de 75 mil artículos a la base de datos cada año. La abrumadora mayoría de las obras en este océano contienen nuevos teoremas matemáticos y sus pruebas ".
Etimología
La palabra matemática proviene del griego antiguo μάθημα ( máthēma ), que significa "lo que se aprende", "lo que uno llega a saber", de ahí también "estudio" y "ciencia". La palabra para "matemáticas" llegó a tener el significado más estricto y más técnico de "estudio matemático", incluso en tiempos clásicos. Su adjetivo es μαθηματικός ( mathēmatikós ), que significa "relacionado con el aprendizaje" o "estudioso", que también vino a significar "matemático". En particular, μαθηματικὴ τέχνη ( mathēmatikḗ tékhnē ), latín: ars mathematica , significaba "el arte matemático".
De manera similar, una de las dos escuelas principales de pensamiento en el pitagorismo era conocida como mathēmatikoi (μαθηματικοί), que en ese momento significaba "maestros" en lugar de "matemáticos" en el sentido moderno.
En latín, y en inglés hasta alrededor de 1700, el término matemáticas más comúnmente significaba "astrología" (o algunas veces "astronomía") en lugar de "matemáticas"; el significado cambió gradualmente al actual de aproximadamente 1500 a 1800. Esto ha resultado en varias traducciones erróneas. Por ejemplo, la advertencia de San Agustín de que los cristianos deben tener cuidado con los matemáticos , es decir, los astrólogos, a veces se traduce erróneamente como una condena de los matemáticos.
La forma plural aparente en inglés, como la forma francesa plural les mathématiques (y la derivada singular menos común la mathématique ), se remonta al latín neutro plural mathematica (Cicero), basado en el plural griego τα μαθηματικά ( ta mathēmatiká ), utilizado por Aristóteles (384-322 aC), y que significa aproximadamente "todas las cosas matemáticas"; aunque es verosímil que el inglés tomara prestado solamente el adjetivo matemático (al) y formara el sustantivo matemático de nuevo, según el patrón de la física y la metafísica , que se heredaron del griego. En inglés, el sustantivo matemático toma un verbo en singular A menudo se abrevia a las matemáticas o, en América del Norte, a las matemáticas .
Definiciones de Matemáticas
Aristóteles definió las matemáticas como "la ciencia de la cantidad", y esta definición prevaleció hasta el siglo XVIII. A partir del siglo XIX, cuando el estudio de las matemáticas aumentó en rigor y comenzó a abordar temas abstractos como teoría de grupos y geometría proyectiva, que no tienen una relación clara con la cantidad y la medición, los matemáticos y filósofos comenzaron a proponer una variedad de nuevas definiciones. Algunas de estas definiciones enfatizan el carácter deductivo de gran parte de las matemáticas, algunas enfatizan su abstracción, otras enfatizan ciertos temas dentro de las matemáticas. Hoy en día, ningún consenso sobre la definición de las matemáticas prevalece, incluso entre los profesionales. Ni siquiera hay consenso sobre si las matemáticas son un arte o una ciencia. Muchos matemáticos profesionales no se interesan en una definición de matemáticas, o lo consideran indefinible Algunos solo dicen: "Las matemáticas son lo que hacen los matemáticos".
Tres tipos principales de definición de las matemáticas se llaman logicista, intuicionista y formalista, cada uno reflejando una escuela filosófica de pensamiento diferente. Todos tienen problemas graves, ninguno tiene una aceptación generalizada y no parece posible la reconciliación.
Una definición temprana de las matemáticas en términos de lógica fue "la ciencia que saca conclusiones necesarias" de Benjamin Peirce (1870). En los Principia Mathematica , Bertrand Russell y Alfred North Whitehead avanzaron en el programa filosófico conocido como logicismo e intentaron demostrar que todos los conceptos matemáticos, enunciados y principios pueden definirse y demostrarse completamente en términos de lógica simbólica. Una definición logicista de las matemáticas es "Todas las matemáticas es una lógica simbólica" de Russell (1903).
Las definiciones intuicionistas, que se desarrollan a partir de la filosofía del matemático LEJ Brouwer, identifican las matemáticas con ciertos fenómenos mentales. Un ejemplo de definición intuicionista es "Las matemáticas son la actividad mental que consiste en llevar a cabo constructos uno después del otro". Una peculiaridad del intuicionismo es que rechaza algunas ideas matemáticas consideradas válidas de acuerdo con otras definiciones. En particular, mientras que otras filosofías de las matemáticas permiten que los objetos puedan demostrarse que existen aunque no se puedan construir, el intuicionismo solo permite objetos matemáticos que uno realmente puede construir.
Las definiciones formalistas identifican las matemáticas con sus símbolos y las reglas para operar en ellas. Haskell Curry definió las matemáticas simplemente como "la ciencia de los sistemas formales". Un sistema formal es un conjunto de símbolos, o tokens , y algunas reglas que indican cómo los tokens se pueden combinar en fórmulas . En los sistemas formales, la palabra axioma tiene un significado especial, diferente del significado ordinario de "una verdad evidente por sí misma". En los sistemas formales, un axioma es una combinación de tokens que se incluye en un sistema formal dado sin necesidad de derivarlo utilizando las reglas del sistema.
Matemáticas como ciencia
El matemático alemán Carl Friedrich Gauss se refirió a las matemáticas como "la Reina de las Ciencias". Más recientemente, Marcus du Sautoy ha llamado a las matemáticas "la Reina de la Ciencia ... la principal fuerza detrás del descubrimiento científico". En el latín original Regina Scientiarum , así como en el alemán Königin der Wissenschaften , la palabra correspondiente a la ciencia significa un "campo de conocimiento", y este fue también el significado original de "ciencia" en inglés; las matemáticas son en este sentido un campo de conocimiento. La especialización que restringe el significado de "ciencia" a las ciencias naturales sigue el auge de la ciencia baconiana, que contrastó la "ciencia natural" con la escolástica, el método aristotélico de indagar desde los primeros principios. El papel de la experimentación empírica y la observación es insignificante en matemáticas, en comparación con las ciencias naturales como la biología, la química o la física. Albert Einstein afirmó que "en la medida en que las leyes de las matemáticas se refieren a la realidad, no son ciertas y, en la medida en que son ciertas, no se refieren a la realidad".
Muchos filósofos creen que las matemáticas no son falsables experimentalmente, y por lo tanto no son una ciencia según la definición de Karl Popper. Sin embargo, en la década de 1930, los teoremas de incompletitud de Gödel convencieron a muchos matemáticos de que las matemáticas no pueden reducirse a la lógica, y Karl Popper concluyó que "la mayoría de las teorías matemáticas son, como las de la física y la biología, hipotético-deductivas: las matemáticas puras resultan ser mucho más cerca de las ciencias naturales, cuyas hipótesis son conjeturas, de lo que parecía hasta hace poco ". Otros pensadores, especialmente Imre Lakatos, han aplicado una versión del falsacionismo a las matemáticas mismas.
Una visión alternativa es que ciertos campos científicos (como la física teórica) son matemáticas con axiomas que pretenden corresponder a la realidad. Las matemáticas comparten mucho en común con muchos campos en las ciencias físicas, especialmente la exploración de las consecuencias lógicas de las suposiciones. La intuición y la experimentación también juegan un papel en la formulación de conjeturas tanto en las matemáticas como en las (otras) ciencias. Las matemáticas experimentales continúan creciendo en importancia dentro de las matemáticas, y la computación y la simulación están desempeñando un papel cada vez más importante tanto en las ciencias como en las matemáticas.
Las opiniones de los matemáticos sobre este tema son variadas. Muchos matemáticos sienten que llamar ciencia a su área es minimizar la importancia de su lado estético y su historia en las siete artes liberales tradicionales; otros sienten que ignorar su conexión con las ciencias es hacer la vista gorda ante el hecho de que la interfaz entre las matemáticas y sus aplicaciones en ciencia e ingeniería ha impulsado mucho el desarrollo en matemáticas. Una forma en que esta diferencia de punto de vista se manifiesta es en el debate filosófico sobre si las matemáticas se crean (como en el arte) o si se descubren (como en la ciencia). Es común ver las universidades divididas en secciones que incluyen una división de Ciencias y Matemáticas, lo que indica que los campos se ven como aliados pero que no coinciden. En la práctica, los matemáticos suelen agruparse con científicos en el nivel bruto, pero separados en niveles más finos. Este es uno de los muchos temas considerados en la filosofía de las matemáticas.
Inspiración, matemáticas puras y aplicadas, y estética
Las matemáticas surgen de muchos tipos diferentes de problemas. Al principio, estos se encontraron en el comercio, la medición de la tierra, la arquitectura y la astronomía posterior; hoy, todas las ciencias sugieren problemas estudiados por los matemáticos, y surgen muchos problemas dentro de las matemáticas mismas. Por ejemplo, el físico Richard Feynman inventó la formulación integral del camino de la mecánica cuántica usando una combinación de razonamiento matemático y perspicacia física, y la teoría de cuerdas de hoy, una teoría científica todavía en desarrollo que intenta unificar las cuatro fuerzas fundamentales de la naturaleza, continúa inspirando nuevas matemáticas.
Algunas matemáticas solo son relevantes en el área que las inspiró, y se aplican para resolver otros problemas en esa área. Pero a menudo las matemáticas inspiradas en un área resultan útiles en muchas áreas y se unen al conjunto general de conceptos matemáticos. A menudo se hace una distinción entre las matemáticas puras y las matemáticas aplicadas. Sin embargo, los temas puramente matemáticos suelen tener aplicaciones, por ejemplo, teoría de números en criptografía. Este hecho notable, que incluso las matemáticas "más puras" a menudo resultan tener aplicaciones prácticas, es lo que Eugene Wigner ha llamado "la efectividad irrazonable de las matemáticas". Como en la mayoría de las áreas de estudio, la explosión de conocimiento en la era científica ha llevado a la especialización: ahora hay cientos de áreas especializadas en matemáticas y la última Clasificación de materias de Matemáticas tiene una extensión de 46 páginas. Varias áreas de las matemáticas aplicadas se han fusionado con tradiciones relacionadas fuera de las matemáticas y se han convertido en disciplinas por derecho propio, que incluyen estadísticas, investigación operativa y ciencias de la computación.
Para aquellos que están matemáticamente inclinados, a menudo hay un aspecto estético definido en gran parte de las matemáticas. Muchos matemáticos hablan sobre la elegancia de las matemáticas, su estética intrínseca y su belleza interior. Simplicidad y generalidad son valorados. Hay belleza en una prueba simple y elegante, como la prueba de Euclides de que hay infinitos números primos, y en un elegante método numérico que acelera el cálculo, como la transformada rápida de Fourier. GH Hardy en la disculpa de un matemático expresó la creencia de que estas consideraciones estéticas son, en sí mismas, suficientes para justificar el estudio de las matemáticas puras. Identificó criterios tales como significancia, inesperado, inevitabilidad y economía como factores que contribuyen a una estética matemática. Los matemáticos a menudo se esfuerzan por encontrar pruebas que sean particularmente elegantes, pruebas del "Libro" de Dios según Paul Erdős. La popularidad de las matemáticas recreativas es otro signo del placer que muchos encuentran al resolver preguntas matemáticas.
Notación, lenguaje y rigor
La mayor parte de la notación matemática en uso hoy en día no se inventó hasta el siglo XVI. Antes de eso, las matemáticas se escribían con palabras, lo que limitaba el descubrimiento matemático. Euler (1707-1783) fue responsable de muchas de las anotaciones actualmente en uso. La notación moderna hace que las matemáticas sean mucho más fáciles para el profesional, pero a los principiantes a menudo les resulta desalentador. Según Barbara Oakley, esto se puede atribuir al hecho de que las ideas matemáticas son más abstractas y más encriptadas que las del lenguaje natural. A diferencia del lenguaje natural, donde las personas a menudo pueden equiparar una palabra (como vaca) con el objeto físico al que corresponde, los símbolos matemáticos son abstractos, carecen de cualquier análogo físico. Los símbolos matemáticos también están más altamente encriptados que las palabras regulares, lo que significa que un solo símbolo puede codificar una cantidad de operaciones o ideas diferentes.
El lenguaje matemático puede ser difícil de entender para los principiantes, ya que incluso los términos más comunes, tales como o y única , tiene un significado más preciso de lo que tienen en el lenguaje cotidiano, y otros términos tales como abierta y campo de referirse a las ideas matemáticas específicas, no cubierto por su los significados de los legos. El lenguaje matemático también incluye muchos términos técnicos tales como homeomorfismo e integrable que no tienen significado fuera de las matemáticas. Además, frases abreviadas como iff para "si y solo si" pertenece a la jerga matemática. Hay una razón para la notación especial y el vocabulario técnico: las matemáticas requieren más precisión que el habla cotidiana. Los matemáticos se refieren a esta precisión de lenguaje y lógica como "rigor".
La prueba matemática es fundamentalmente una cuestión de rigor. Los matemáticos quieren que sus teoremas se sigan a partir de axiomas por medio de un razonamiento sistemático. Esto es para evitar "teoremas" equivocados, basados en intuiciones falibles, de las cuales muchas instancias han ocurrido en la historia del sujeto. El nivel de rigor esperado en las matemáticas ha variado con el tiempo: los griegos esperaban argumentos detallados, pero en la época de Isaac Newton los métodos empleados eran menos rigurosos. Los problemas inherentes a las definiciones utilizadas por Newton conducirían a un resurgimiento del análisis cuidadoso y la prueba formal en el siglo XIX. El malentendido del rigor es la causa de algunos de los conceptos erróneos comunes de las matemáticas. Hoy, los matemáticos continúan discutiendo entre ellos acerca de las pruebas asistidas por computadora. Dado que los cálculos grandes son difíciles de verificar,
Los axiomas en el pensamiento tradicional son "verdades evidentes por sí mismos", pero esa concepción es problemática. En un nivel formal, un axioma es solo una cadena de símbolos, que tiene un significado intrínseco solo en el contexto de todas las fórmulas derivables de un sistema axiomático. El objetivo del programa de Hilbert era poner todas las matemáticas en una base axiomática firme, pero de acuerdo con el teorema de la incompletitud de Gödel cada sistema axiomático (suficientemente poderoso) tiene fórmulas indecidibles; y entonces una axiomatización final de las matemáticas es imposible. No obstante, a menudo se imagina que las matemáticas (en cuanto a su contenido formal) no son nada más que teoría de conjuntos en alguna axiomatización, en el sentido de que cada enunciado o prueba matemática podría convertirse en fórmulas dentro de la teoría de conjuntos.
Campos de las matemáticas
Las matemáticas pueden, en términos generales, subdividirse en el estudio de la cantidad, estructura, espacio y cambio (es decir, aritmética, álgebra, geometría y análisis). Además de estas preocupaciones principales, también hay subdivisiones dedicadas a explorar enlaces desde el corazón de las matemáticas a otros campos: a la lógica, a la teoría de conjuntos (fundamentos), a las matemáticas empíricas de las diversas ciencias (matemáticas aplicadas), y más recientemente al estudio riguroso de la incertidumbre. Mientras que algunas áreas pueden parecer no relacionadas, el programa Langlands ha encontrado conexiones entre áreas que anteriormente se consideraban desconectadas, como los grupos de Galois, las superficies de Riemann y la teoría de los números.
Fundamentos y filosofía
Para aclarar los fundamentos de las matemáticas, se desarrollaron los campos de la lógica matemática y la teoría de conjuntos. La lógica matemática incluye el estudio matemático de la lógica y las aplicaciones de la lógica formal a otras áreas de las matemáticas; La teoría de conjuntos es la rama de las matemáticas que estudia las colecciones de conjuntos de objetos. La teoría de categorías, que trata de una manera abstracta con las estructuras matemáticas y las relaciones entre ellos, todavía está en desarrollo. La frase "crisis de los fundamentos" describe la búsqueda de una base rigurosa para las matemáticas que tuvo lugar aproximadamente desde 1900 hasta 1930. Algunos desacuerdos sobre los fundamentos de las matemáticas continúan hasta nuestros días. La crisis de las fundaciones fue estimulada por una serie de controversias en el momento, incluida la controversia sobre Cantor '
La lógica matemática se ocupa de establecer las matemáticas dentro de un marco axiomático riguroso y estudiar las implicaciones de dicho marco. Como tal, es el hogar de los teoremas de incompletitud de Gödel que (informalmente) implican que cualquier sistema formal efectivo que contenga aritmética básica, si es correcto (lo que significa que todos los teoremas que pueden probarse son verdaderos), es necesariamente incompleto (lo que significa que hay verdaderos teoremas que no puede ser probado en ese sistema) Cualquiera que sea la colección finita de axiomas teóricos de los números que se tome como base, Gödel mostró cómo construir una declaración formal que es un verdadero hecho teórico-numérico, pero que no se sigue de esos axiomas. Por lo tanto, ningún sistema formal es una axiomatización completa de la teoría de los números completos. La lógica moderna se divide en teoría de la recursión, teoría del modelo y teoría de la prueba, y está estrechamente vinculada a la informática teórica, así como a la teoría de categorías. En el contexto de la teoría de la recursión, la imposibilidad de una axiomatización completa de la teoría numérica también se puede demostrar formalmente como una consecuencia del teorema MRDP.
La informática teórica incluye la teoría de la computabilidad, la teoría de la complejidad computacional y la teoría de la información. La teoría de la computabilidad examina las limitaciones de varios modelos teóricos de la computadora, incluido el modelo más conocido: la máquina de Turing. La teoría de la complejidad es el estudio de la capacidad de tratamiento por computadora; algunos problemas, aunque son teóricamente solucionables por computadora, son tan caros en términos de tiempo o espacio que su solución es probable que permanezca prácticamente inviable, incluso con el rápido avance del hardware de la computadora. Un problema famoso es el "
P = NP ?"problema, uno de los problemas del Premio Milenio. Por último, la teoría de la información se refiere a la cantidad de datos que se pueden almacenar en un medio determinado, y por lo tanto se ocupa de conceptos como la compresión y la entropía.
P = NP ?"problema, uno de los problemas del Premio Milenio. Por último, la teoría de la información se refiere a la cantidad de datos que se pueden almacenar en un medio determinado, y por lo tanto se ocupa de conceptos como la compresión y la entropía.



Lógica matemática Teoría de conjuntos Teoría de categorías Teoría de la computación
Matemáticas puras
Cantidad
El estudio de la cantidad comienza con números, primero los números naturales familiares y enteros ("números enteros") y operaciones aritméticas sobre ellos, que se caracterizan en aritmética. Las propiedades más profundas de los enteros se estudian en la teoría de números, de la cual provienen resultados tan populares como el último teorema de Fermat. La conjetura principal doble y la conjetura de Goldbach son dos problemas sin resolver en la teoría de números.
A medida que el sistema numérico se desarrolla aún más, los enteros se reconocen como un subconjunto de los números racionales ("fracciones"). Estos, a su vez, están contenidos dentro de los números reales, que se usan para representar cantidades continuas. Los números reales se generalizan a números complejos. Estos son los primeros pasos de una jerarquía de números que incluye cuaterniones y octoniones. La consideración de los números naturales también conduce a los números transfinitos, que formalizan el concepto de "infinito". De acuerdo con el teorema fundamental del álgebra, todas las soluciones de ecuaciones en una desconocida con coeficientes complejos son números complejos, independientemente de su grado. Otra área de estudio es el tamaño de los conjuntos, que se describe con los números cardinales. Estos incluyen los números aleph,
Números naturales Enteros Numeros racionales Numeros reales Números complejos
Estructura
Muchos objetos matemáticos, como conjuntos de números y funciones, exhiben una estructura interna como consecuencia de las operaciones o relaciones que se definen en el conjunto. Luego, las matemáticas estudian las propiedades de esos conjuntos que se pueden expresar en términos de esa estructura; por ejemplo, la teoría numérica estudia las propiedades del conjunto de enteros que pueden expresarse en términos de aritmética. Además, sucede con frecuencia que diferentes conjuntos estructurados (o estructuras) exhiben propiedades similares, lo que hace posible, mediante un paso más de abstracción, establecer axiomas para una clase de estructuras, y luego estudiar a la vez toda la clase de estructuras que satisfacen estos axiomas. Por lo tanto, uno puede estudiar grupos, anillos, campos y otros sistemas abstractos;
Por su gran generalidad, el álgebra abstracta a menudo se puede aplicar a problemas aparentemente no relacionados; por ejemplo, una serie de antiguos problemas relativos a las construcciones de compás y regla no se resolvió finalmente utilizando la teoría de Galois, que implica la teoría de campo y la teoría de grupos. Otro ejemplo de una teoría algebraica es el álgebra lineal, que es el estudio general de los espacios de vectores, cuyos elementos llamados vectores tienen tanto cantidad como dirección, y pueden usarse para modelar (relaciones entre) puntos en el espacio. Este es un ejemplo del fenómeno de que las áreas de geometría y álgebra, originalmente no relacionadas, tienen interacciones muy fuertes en las matemáticas modernas. Combinatorics estudia formas de enumerar el número de objetos que se ajustan a una estructura determinada.




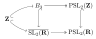
Combinatorios Teoría de los números Teoría de grupo Teoría de grafos Teoría del pedido Álgebra
Espacio
El estudio del espacio se origina con la geometría, en particular, la geometría euclidiana, que combina espacio y números, y abarca el bien conocido teorema de Pitágoras. La trigonometría es la rama de las matemáticas que se ocupa de las relaciones entre los lados y los ángulos de los triángulos y con las funciones trigonométricas. El estudio moderno del espacio generaliza estas ideas para incluir la geometría de mayor dimensión, las geometrías no euclidianas (que desempeñan un papel central en la relatividad general) y la topología. La cantidad y el espacio juegan un papel en la geometría analítica, la geometría diferencial y la geometría algebraica. La geometría convexa y discreta se desarrolló para resolver problemas en la teoría de números y el análisis funcional, pero ahora se persiguen con un ojo puesto en las aplicaciones de optimización y ciencias de la computación. Dentro de la geometría diferencial se encuentran los conceptos de paquetes de fibra y cálculo en variedades, en particular, cálculo vectorial y de tensor. Dentro de la geometría algebraica se encuentra la descripción de objetos geométricos como conjuntos de soluciones de ecuaciones polinómicas, que combinan los conceptos de cantidad y espacio, y también el estudio de grupos topológicos, que combinan estructura y espacio. Los grupos de Lie se utilizan para estudiar el espacio, la estructura y el cambio. La topología en todas sus ramificaciones puede haber sido la mayor área de crecimiento en las matemáticas del siglo XX; incluye topología de punto de referencia, topología teórica de conjunto, topología algebraica y topología diferencial. En particular, las instancias de la topología moderna son la teoría de la metrizabilidad, la teoría axiomática de conjuntos, la teoría de la homotopía y la teoría Morse. La topología también incluye la conjetura de Poincaré ahora resuelta, y las áreas aún no resueltas de la conjetura de Hodge. Otros resultados en geometría y topología, incluyendo el teorema de cuatro colores y la conjetura de Kepler, se han demostrado solo con la ayuda de computadoras.






Geometría Trigonometría Geometría diferencial Topología Geometría Fractal Teoría de medida
Cambio
Comprender y describir el cambio es un tema común en las ciencias naturales, y el cálculo se desarrolló como una poderosa herramienta para investigarlo. Las funciones surgen aquí, como un concepto central que describe una cantidad cambiante. El estudio riguroso de los números reales y las funciones de una variable real se conoce como análisis real, y el análisis complejo es el campo equivalente para los números complejos. El análisis funcional enfoca la atención en espacios de funciones (típicamente de dimensión infinita). Una de las muchas aplicaciones del análisis funcional es la mecánica cuántica. Muchos problemas conducen naturalmente a las relaciones entre una cantidad y su tasa de cambio, y estos se estudian como ecuaciones diferenciales. Muchos fenómenos en la naturaleza pueden ser descritos por sistemas dinámicos;
 |  |  |  |  |  |
| Cálculo | Cálculo de vectores | Ecuaciones diferenciales | Sistemas dinámicos | Teoría del caos | Análisis complejo |
Matemáticas Aplicadas
Las matemáticas aplicadas se refieren a sí mismas con métodos matemáticos que normalmente se usan en ciencia, ingeniería, negocios e industria. Por lo tanto, "matemáticas aplicadas" es una ciencia matemática con conocimiento especializado. El término matemática aplicada también describe la especialidad profesional en la que los matemáticos trabajan en problemas prácticos; como una profesión enfocada en problemas prácticos, las matemáticas aplicadas se enfocan en la "formulación, estudio y uso de modelos matemáticos" en ciencias, ingeniería y otras áreas de la práctica matemática.
En el pasado, las aplicaciones prácticas han motivado el desarrollo de teorías matemáticas, que luego se convirtieron en el tema de estudio en las matemáticas puras, donde las matemáticas se desarrollan principalmente por sí mismas. Por lo tanto, la actividad de las matemáticas aplicadas está vitalmente relacionada con la investigación en matemáticas puras.
Estadísticas y otras ciencias de decisión
Las matemáticas aplicadas tienen una superposición significativa con la disciplina de la estadística, cuya teoría se formula matemáticamente, especialmente con la teoría de la probabilidad. Los estadísticos (que trabajan como parte de un proyecto de investigación) "crean datos que tienen sentido" con muestreo aleatorio y con experimentos aleatorios; el diseño de una muestra estadística o experimento especifica el análisis de los datos (antes de que los datos estén disponibles). Al reconsiderar datos de experimentos y muestras o al analizar datos de estudios observacionales, los estadísticos "dan sentido a los datos" utilizando el arte del modelado y la teoría de la inferencia, con la selección y estimación del modelo; los modelos estimados y las predicciones consiguientes deberían probarse con nuevos datos.
La teoría estadística estudia problemas de decisión tales como minimizar el riesgo (pérdida esperada) de una acción estadística, como usar un procedimiento en, por ejemplo, estimación de parámetros, prueba de hipótesis y selección de los mejores. En estas áreas tradicionales de estadística matemática, se formula un problema de decisión estadística al minimizar una función objetiva, como pérdida o costo esperado, bajo restricciones específicas: por ejemplo, diseñar una encuesta a menudo implica minimizar el costo de estimar una media poblacional con un determinado nivel de confianza. Debido a su uso de la optimización, la teoría matemática de la estadística comparte preocupaciones con otras ciencias de decisión, como la investigación de operaciones, la teoría de control y la economía matemática.
Matemática computacional
Las matemáticas computacionales proponen y estudian métodos para resolver problemas matemáticos que normalmente son demasiado grandes para la capacidad numérica humana. El análisis numérico estudia los métodos para los problemas en el análisis utilizando el análisis funcional y la teoría de aproximación; el análisis numérico incluye el estudio de la aproximación y la discretización en general, con especial preocupación por los errores de redondeo. El análisis numérico y, más ampliamente, la computación científica también estudian los temas no analíticos de la ciencia matemática, especialmente la matriz algorítmica y la teoría de grafos. Otras áreas de las matemáticas computacionales incluyen álgebra computacional y computación simbólica.
 |  |  |  |  | ||
| Teoría de juego | Dinámica de fluidos | Análisis numérico | Mejoramiento | Teoría de probabilidad | Estadística | Criptografía |
 |  | 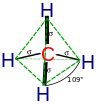 |  | |||
| Finanzas Matemáticas | Física matemática | Química matemática | Biología matemática | Economía matemática | Teoría de control |
Premios matemáticos
Podría decirse que el premio más prestigioso en matemáticas es la Medalla Fields, establecida en 1936 y otorgada cada cuatro años (excepto en torno a la Segunda Guerra Mundial) a un máximo de cuatro personas. La medalla Fields a menudo se considera un equivalente matemático al Premio Nobel.
El Premio Wolf en Matemáticas, instituido en 1978, reconoce el logro de toda una vida, y otro importante premio internacional, el Premio Abel, se instituyó en 2003. La Medalla Chern se introdujo en 2010 para reconocer el logro de toda una vida. Estos galardones se otorgan en reconocimiento de un cuerpo de trabajo particular, que puede ser innovador o proporcionar una solución a un problema pendiente en un campo establecido.
Una lista famosa de 23 problemas abiertos, llamados "problemas de Hilbert", fue compilada en 1900 por el matemático alemán David Hilbert. Esta lista alcanzó gran celebridad entre los matemáticos, y al menos nueve de los problemas se han resuelto. Una nueva lista de siete problemas importantes, titulada "Problemas del Premio del Milenio", se publicó en 2000. Solo uno de ellos, la hipótesis de Riemann, duplica uno de los problemas de Hilbert. Una solución a cualquiera de estos problemas conlleva una recompensa de $ 1 millón.
















