Trigonometría
Definición
La trigonometría (del griego trigonom , "triángulo" y metrón , "medida") es una rama de las matemáticas que estudia las relaciones que involucran longitudes y ángulos de triángulos. El campo surgió en el mundo helenístico durante el siglo III aC desde las aplicaciones de la geometría hasta los estudios astronómicos.
Los astrónomos del siglo III primero notaron que las longitudes de los lados de un triángulo en ángulo recto y los ángulos entre esos lados tienen relaciones fijas: es decir, si se conoce al menos la longitud de un lado y el valor de un ángulo, entonces todos los demás ángulos y longitudes pueden determinarse algorítmicamente. Estos cálculos pronto se definieron como las funciones trigonométricas y hoy en día son omnipresentes tanto en matemáticas puras como aplicadas: métodos fundamentales de análisis como la transformada de Fourier, por ejemplo, o la ecuación de onda, usan funciones trigonométricas para comprender fenómenos cíclicos en muchas aplicaciones en campos tan diversos como la física, la ingeniería mecánica y eléctrica, la música y la acústica, la astronomía, la ecología y la biología. La trigonometría es también la base de la topografía.
La trigonometría se asocia más simplemente con triángulos de ángulo recto planos (cada uno de los cuales es un triángulo bidimensional con un ángulo igual a 90 grados). La aplicabilidad a triángulos no en ángulo recto existe, pero, dado que cualquier triángulo no en ángulo recto (en un plano) se puede dividir en dos para crear dos triángulos en ángulo recto, la mayoría de los problemas se pueden reducir a cálculos en triángulos en ángulo recto . Por lo tanto, la mayoría de las aplicaciones se relacionan con triángulos en ángulo recto. Una excepción a esto es la trigonometría esférica, el estudio de triángulos en esferas, superficies de curvatura positiva constante, en geometría elíptica (una parte fundamental de la astronomía y la navegación). La trigonometría en superficies de curvatura negativa es parte de la geometría hiperbólica.
Los conceptos básicos de trigonometría a menudo se enseñan en las escuelas, ya sea como un curso separado o como parte de un curso de precalculo.
Historia
Una concha de anillo grueso en el sitio de la civilización del valle del Indo de Lothal, con cuatro ranuras cada una en dos márgenes, sirve como una brújula para medir ángulos en superficies planas o en el horizonte en múltiplos de 40 grados, hasta 360 grados. Tales instrumentos de concha fueron probablemente inventados para medir 8-12 secciones enteras del horizonte y el cielo, lo que explica las hendiduras en los márgenes inferior y superior. Los arqueólogos consideran esto como evidencia de que los expertos de Lothal habían logrado una división de horizonte y cielo de 8 a 12 veces, así como un instrumento para medir ángulos y tal vez la posición de las estrellas, y para la navegación.
Los astrónomos sumerios estudiaron la medida del ángulo, usando una división de círculos en 360 grados. Ellos, y más tarde los babilonios, estudiaron las proporciones de los lados de triángulos similares y descubrieron algunas propiedades de estas proporciones, pero no lo convirtieron en un método sistemático para encontrar lados y ángulos de triángulos. Los antiguos nubios usaban un método similar.
En el siglo III aC, los matemáticos helenísticos como Euclides y Arquímedes estudiaron las propiedades de los acordes y los ángulos inscritos en círculos, y probaron teoremas que son equivalentes a las fórmulas trigonométricas modernas, aunque los presentaron de forma geométrica en lugar de algebraicamente. En 140 a. C., Hiparco (de Nicea, Asia Menor) dio las primeras tablas de acordes, análogas a las tablas modernas de valores sinusoidales, y las utilizó para resolver problemas en trigonometría y trigonometría esférica. En el siglo II dC, el astrónomo greco-egipcio Ptolemeo (de Alejandría, Egipto) construyó tablas trigonométricas detalladas (la tabla de acordes de Ptolomeo) en el Libro 1, capítulo 11 de su Almagesto. Ptolomeo usó la longitud de la cuerda para definir sus funciones trigonométricas, una diferencia menor de la convención seno que usamos hoy. (El valor que llamamos sin (θ) puede encontrarse buscando la longitud de la cuerda para el doble del ángulo de interés (2θ) en la tabla de Ptolomeo, y luego dividiendo ese valor por dos). Pasaron siglos antes de que se produjeran tablas más detalladas, y El tratado de Ptolomeo permaneció en uso para realizar cálculos trigonométricos en astronomía a lo largo de los siguientes 1200 años en los mundos medieval bizantino, islámico y, más tarde, europeo occidental.
La convención seno moderna se atestigua por primera vez en el Surya Siddhanta , y sus propiedades fueron documentadas por el matemático y astrónomo indio Aryabhata, del siglo quinto (AD). Estas obras griegas e indias fueron traducidas y ampliadas por matemáticos medievales islámicos. En el siglo X, los matemáticos islámicos usaban las seis funciones trigonométricas, tabulaban sus valores y los aplicaban a los problemas de la geometría esférica. Casi al mismo tiempo, los matemáticos chinos desarrollaron la trigonometría de forma independiente, aunque no era un campo de estudio importante para ellos. El conocimiento de las funciones y métodos trigonométricos llegó a Europa occidental a través de traducciones al latín del Almagesto griego de Ptolomeo así como los trabajos de astrónomos persas y árabes como Al Battani y Nasir al-Din al-Tusi. Una de las primeras obras sobre trigonometría de un matemático del norte de Europa es De Triangulis, del matemático alemán Regiomontanus del siglo XV, quien fue animado a escribir, y provisto con una copia del Almagesto , por el erudito bizantino cardinal griego Basilios Bessarion con quien vivió por muchos años. Al mismo tiempo, el cretense Jorge de Trebisonda completó otra traducción del Almagesto del griego al latín. La trigonometría todavía era tan poco conocida en el norte de Europa del siglo XVI que Nicolaus Copérnico dedicó dos capítulos de De revolutionibus orbium coelestium para explicar sus conceptos básicos.
Impulsada por las exigencias de la navegación y la creciente necesidad de mapas precisos de grandes áreas geográficas, la trigonometría se convirtió en una importante rama de las matemáticas. Bartholomaeus Pitiscus fue el primero en usar la palabra, publicando su Trigonometria en 1595. Gemma Frisius describió por primera vez el método de triangulación que todavía se usa en la topografía. Fue Leonhard Euler quien incorporó completamente los números complejos en la trigonometría. Las obras de los matemáticos escoceses James Gregory en el siglo XVII y Colin Maclaurin en el siglo XVIII influyeron en el desarrollo de las series trigonométricas. También en el siglo XVIII, Brook Taylor definió la serie general de Taylor.
Visión de conjunto
Si un ángulo de un triángulo es de 90 grados y se conoce uno de los otros ángulos, el tercero es fijo, porque los tres ángulos de cualquier triángulo suman 180 grados. Los dos ángulos agudos, por lo tanto, suman 90 grados: son ángulos complementarios. La forma de un triángulo está completamente determinada, a excepción de la similitud, por los ángulos. Una vez que se conocen los ángulos, se determinan las relaciones de los lados, independientemente del tamaño total del triángulo. Si se conoce la longitud de uno de los lados, se determinan los otros dos. Estas relaciones están dadas por las siguientes funciones trigonométricas del ángulo conocido A , donde un , b y c se refieren a las longitudes de los lados en la figura adjunta:
- Función seno (sin), definida como la relación del lado opuesto al ángulo de la hipotenusa.
- Función coseno (cos), definida como la relación entre la pierna adyacente y la hipotenusa.
- Función tangente (tan), definida como la relación entre la pierna opuesta y la pierna adyacente.
La hipotenusa es el lado opuesto al ángulo de 90 grados en un triángulo rectángulo; es el lado más largo del triángulo y uno de los dos lados adyacentes a ángulo A . La pata adyacente es el otro lado que es adyacente al ángulo A . El lado opuesto es el lado que es opuesto al ángulo A . Los términos perpendicular y base a veces se usan para los lados opuesto y adyacente, respectivamente. A muchas personas les resulta fácil recordar qué lados del triángulo rectángulo son iguales a seno, coseno o tangente, al memorizar la palabra SOH-CAH-TOA (ver abajo debajo de Mnemónicos).
Los recíprocos de estas funciones se denominan cosecante (csc o cosec), secante (seg) y cotangente (cot), respectivamente:
Las funciones inversas se llaman arcoseno , arcocoseno y arcotangente , respectivamente. Hay relaciones aritméticas entre estas funciones, que se conocen como identidades trigonométricas. El coseno, la cotangente y la cosecante se llaman así porque son, respectivamente, el seno, la tangente y la secante del ángulo complementario abreviado como "co".
Con estas funciones, uno puede responder virtualmente a todas las preguntas sobre triángulos arbitrarios usando la ley de los senos y la ley de los cosenos. Estas leyes se pueden usar para calcular los ángulos y lados restantes de cualquier triángulo tan pronto como se conozcan dos lados y su ángulo incluido o dos ángulos y un lado o tres lados. Estas leyes son útiles en todas las ramas de la geometría, ya que cada polígono se puede describir como una combinación finita de triángulos.
Extendiendo las definiciones
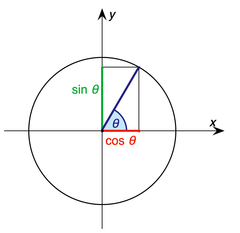
Las definiciones anteriores solo se aplican a ángulos entre 0 y 90 grados (0 y π / 2 radianes). Usando el círculo unitario, uno puede extenderlos a todos los argumentos positivos y negativos (ver función trigonométrica). Las funciones trigonométricas son periódicas, con un período de 360 grados o 2π radianes. Eso significa que sus valores se repiten en esos intervalos. Las funciones de tangente y cotangente también tienen un período más corto, de 180 grados o π radianes.
Las funciones trigonométricas se pueden definir de otras formas además de las definiciones geométricas anteriores, utilizando herramientas de cálculo y series infinitas. Con estas definiciones, las funciones trigonométricas se pueden definir para números complejos. La función exponencial compleja es particularmente útil.
Ver las fórmulas de Euler y De Moivre.
Proceso de gráficas de y = sin ( x ) usando un círculo unitario.
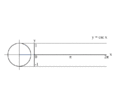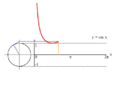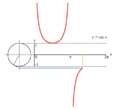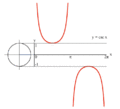Proceso de gráficas de y = csc ( x ), el recíproco de seno, usando un círculo unitario.
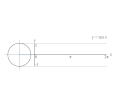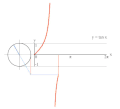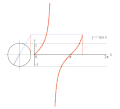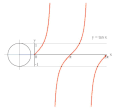Proceso de gráficas de y = tan ( x ) usando un círculo unitario.
Mnemotécnica
Un uso común de mnemotecnia es recordar hechos y relaciones en trigonometría. Por ejemplo, las relaciones seno , coseno y tangente en un triángulo rectángulo pueden recordarse representándolas y sus lados correspondientes como cadenas de letras. Por ejemplo, un mnemónico es SOH-CAH-TOA:
- S ine = O pposite ÷ H ypotenuse
- C osine = A contigua ÷ H ypotenuse
- T angent = O pposite ÷ A contigua
Una forma de recordar las letras es a tocarlas fonéticamente (es decir, SOH-CAH-TOA , que se pronuncia 'so-kə- toe -uh' / s oʊ k ə t oʊ ə / ). Otro método es ampliar las letras en una frase, como " S OMe O ld H ippie C algo A tro H ippie T rippin' O n A cid".
Cálculo de funciones trigonométricas
Las funciones trigonométricas estuvieron entre los primeros usos de tablas matemáticas. Dichas tablas se incorporaron a los libros de texto de matemáticas y se les enseñó a los estudiantes a buscar valores y cómo interpolar entre los valores enumerados para obtener una mayor precisión. Las reglas de diapositiva tenían escalas especiales para funciones trigonométricas.
Hoy en día, las calculadoras científicas tienen botones para calcular las funciones trigonométricas principales (sin, cos, tan, y a veces cis y sus inversas). La mayoría permite una selección de métodos de medición de ángulos: grados, radianes y, a veces, gradianos. La mayoría de los lenguajes de programación de computadoras proporcionan bibliotecas de funciones que incluyen las funciones trigonométricas. El hardware de unidad flotante incorporado en los microprocesadores utilizados en la mayoría de las computadoras personales tiene instrucciones incorporadas para calcular las funciones trigonométricas.
Aplicaciones
Existe una enorme cantidad de usos de trigonometría y funciones trigonométricas. Por ejemplo, la técnica de triangulación se usa en astronomía para medir la distancia a estrellas cercanas, en geografía para medir distancias entre puntos de referencia y en sistemas de navegación por satélite. Las funciones seno y coseno son fundamentales para la teoría de las funciones periódicas, como las que describen las ondas de luz y sonido.
Los campos que usan trigonometría o funciones trigonométricas incluyen astronomía (especialmente para localizar posiciones aparentes de objetos celestes, en los que la trigonometría esférica es esencial) y por lo tanto navegación (en los océanos, en el avión y en el espacio), teoría musical, síntesis de audio, acústica, óptica, electrónica, biología, imagen médica (tomografía computarizada y ultrasonido), farmacia, química, teoría de números (y, por tanto, criptología), sismología, meteorología, oceanografía, muchas ciencias físicas, agrimensura y geodesia, arquitectura, compresión de imagen, fonética, economía , ingeniería eléctrica, ingeniería mecánica, ingeniería civil, gráficos por computadora, cartografía, cristalografía y desarrollo de juegos.
Identidades pitagóricas
Las siguientes identidades están relacionadas con el teorema de Pitágoras y se mantienen por cualquier valor:
Fórmulas de transformación de ángulo
Fórmulas comunes
Ciertas ecuaciones que involucran funciones trigonométricas son verdaderas para todos los ángulos y se conocen como identidades trigonométricas . Algunas identidades equiparan una expresión a una expresión diferente que implica los mismos ángulos. Estos se enumeran en la Lista de identidades trigonométricas. Las identidades del triángulo que relacionan los lados y ángulos de un triángulo dado se enumeran a continuación.
En las siguientes identidades, A , B y C son los ángulos de un triángulo y un , b y c son las longitudes de los lados del triángulo opuesto a los ángulos respectivos (como se muestra en el diagrama).
Ley de los senos
La ley de los senos (también conocida como la "regla sinusoidal") para un triángulo arbitrario establece:
¿Dónde está el área del triángulo y R es el radio del círculo circunscrito del triángulo?
Otra ley que involucra senos se puede usar para calcular el área de un triángulo. Dado dos lados a y b y el ángulo entre los lados C , el área del triángulo está dada por la mitad del producto de las longitudes de dos lados y el seno del ángulo entre los dos lados:
Ley de cosenos
La ley de los cosenos (conocida como la fórmula coseno o la "regla cos") es una extensión del teorema de Pitágoras a triángulos arbitrarios:
o equivalente:
La ley de los cosenos se puede usar para probar la fórmula de Heron, que es otro método que se puede usar para calcular el área de un triángulo. Esta fórmula establece que si un triángulo tiene lados de longitudes a , b y c , y si el semiperímetro es
entonces el área del triángulo es:
- ,
donde R es el radio de la circunferencia circunscrita del triángulo.
Ley de tangentes
La ley de tangentes :
![\ frac {ab} {a + b} = \ frac {\ tan \ left [\ tfrac {1} {2} (AB) \ right]} {\ tan \ left [\ tfrac {1} {2} (A + B) \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1da4e06eb6f25cd7f7fc1a7784a11a82ae53f9f)
Fórmula de Euler
La fórmula de Euler, que establece que , produce las siguientes identidades analíticas para seno, coseno y tangente en términos de e y la unidad imaginaria i :
