Wikiblog Cultulandia [es]

Tipos de secciones cónicas:
1. Parábola
2. Círculo y elipse
3. Hipérbola

Tabla de cónicas, Cyclopaedia , 1728

En matemáticas, una sección cónica (o simplemente cónica ) es una curva obtenida como la intersección de la superficie de un cono con un plano. Los tres tipos de sección cónica son la hipérbola, la parábola y la elipse. El círculo es un caso especial de la elipse, y tiene suficiente interés en sí mismo como para llamarlo a veces un cuarto tipo de sección cónica. Las secciones cónicas han sido estudiadas por los antiguos matemáticos griegos con esta obra que culminó alrededor del año 200 aC, cuando Apolonio de Perga llevó a cabo un estudio sistemático de sus propiedades.

Las secciones cónicas del plano euclidiano tienen varias propiedades distintivas. Muchos de estos se han utilizado como base para una definición de las secciones cónicas. Una de esas propiedades define una cónica no circular como el conjunto de aquellos puntos cuyas distancias a un punto particular, llamado foco , y una línea particular, llamada directriz , están en una relación fija, llamada excentricidad . El tipo de cónica está determinada por el valor de la excentricidad. En la geometría analítica, una cónica se puede definir como una curva algebraica plana de grado 2; es decir, como el conjunto de puntos cuyas coordenadas satisfacen una ecuación cuadrática en dos variables. Esta ecuación se puede escribir en forma de matriz, y algunas propiedades geométricas se pueden estudiar como condiciones algebraicas.

En el plano euclidiano, las secciones cónicas parecen ser bastante diferentes entre sí, pero comparten muchas propiedades. Al extender la geometría a un plano proyectivo (agregando una línea en el infinito), esta aparente diferencia desaparece, y lo común se hace evidente. Una extensión adicional, al expandir las coordenadas reales para admitir coordenadas complejas, proporciona los medios para ver esta unificación algebraicamente.

Geometría euclidiana

Las secciones cónicas se han estudiado durante miles de años y han proporcionado una rica fuente de resultados interesantes y hermosos en geometría euclidiana.

Definición

Los límites negros de las regiones coloreadas son secciones cónicas. No se muestra la otra mitad de la hipérbola, que está en la otra mitad del cono doble.

Una cónica es la curva obtenida como la intersección de un plano, llamado plano de corte , con la superficie de un cono doble (un cono con dos nappes ). Se supondrá que el cono es un cono circular derecho con el fin de facilitar la descripción, pero esto no es necesario; cualquier cono doble con una sección transversal circular será suficiente. Los aviones que pasan por el vértice del cono se cruzan con el cono en un punto, una línea o un par de líneas que se cruzan. Estos se llaman cónicos degenerados y algunos autores no los consideran cónicos en absoluto. A menos que se indique lo contrario, "cónica" en este artículo se referirá a una cónica no degenerada.

Hay tres tipos de cónicas, la elipse, la parábola y la hipérbola. El círculo es un tipo especial de elipse, aunque históricamente se había considerado como un cuarto tipo (como lo fue por Apolonio). El círculo y la elipse surgen cuando la intersección del cono y el plano es una curva cerrada. El círculo se obtiene cuando el plano de corte es paralelo al plano del círculo generador del cono; para un cono derecho, ver diagrama, esto significa que el plano de corte es perpendicular al eje de simetría del cono. Si el plano de corte es paralelo a exactamente una línea generadora del cono, entonces la cónica no tiene límites y se llama parábola . En el caso restante, la figura es una hipérbola . En este caso, el avión se cruza con ambos mitades del cono, produciendo dos curvas separadas sin límites.

Excentricidad, enfoque y directriz

Círculo ( e = 0) , elipse ( e = 1/2 ) , parábola ( e = 1) e hipérbola ( e = 2) con foco fijo F y directriz ( e = ∞) .

Una propiedad que las secciones cónicas comparten a menudo se presenta como la siguiente definición. Una sección cónica es el lugar de todos los puntos

P

cuya distancia a un punto fijo

F

(llamado el foco de la cónica) es un múltiplo constante (llamado excentricidad,

e

) de la distancia de

P

a una línea fija

L

(llamada directriz de la cónica). Para

0 < e <1

obtenemos una elipse, para

e = 1

una parábola, y para

e > 1

una hipérbola.

Un círculo es un caso límite y no está definido por un foco y una directriz en el plano (sin embargo, consulte la sección sobre la extensión a planos proyectivos). La excentricidad de un círculo se define como cero y su foco es el centro del círculo, pero no hay línea en el plano euclidiano que sea su directriz.

Una elipse y una hipérbola tienen dos enfoques y directivas distintas para cada uno de ellos. La línea que une los focos se llama eje principal y los puntos de intersección de la cónica con el eje principal se llaman vértices de la cónica. El segmento de línea que une los vértices de una cónica se denomina eje principal , también llamado eje transversal en la hipérbola. El punto medio de este segmento de línea se llama el centro de la cónica. Deje

a

denotar la distancia desde el centro a un vértice de una elipse o hipérbola. La distancia desde el centro a una directriz es

a / e,

mientras que la distancia desde el centro a un foco es

ae

.

Una parábola no tiene un centro.

La excentricidad de una elipse se puede ver como una medida de cuán lejos se desvía la elipse de ser circular.

Si el ángulo entre la superficie del cono y su eje es y el ángulo entre el plano de corte y el eje es la excentricidad es

\beta

\alfa,

{\ displaystyle {\ frac {\ cos \ alpha} {\ cos \ beta}}.}

Una prueba de que las secciones cónicas dadas por la propiedad focus-directrix son las mismas que las dadas por los planos que intersectan un cono se facilita mediante el uso de las esferas Dandelin.

Parámetros cónicos

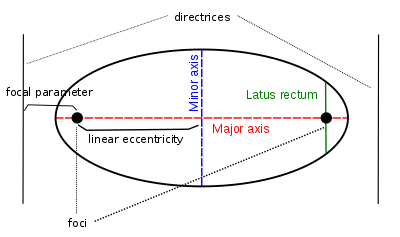
Parámetros cónicos en el caso de una elipse

Varios parámetros están asociados con una sección cónica. Recuerde que el eje principal es la línea que une los focos de una elipse o hipérbola, y el centro en estos casos es el punto medio del segmento de línea que une los focos. Algunas de las otras características comunes y / o parámetros de las cónicas se dan a continuación.

La excentricidad lineal (

c

) es la distancia entre el centro y el foco (o uno de los dos focos).

El latus recum es el acorde paralelo a la directriz y que pasa por el foco (o uno de los dos focos). Su longitud se denota por

2 ℓ

.

El recto semilus (

ℓ

) es la mitad de la longitud del recto latus.

El parámetro focal (

p

) es la distancia desde el foco (o uno de los dos focos) a la directriz.

Cuando una elipse o hipérbola están en posición estándar (el eje principal es el eje

xy

el centro es el origen) los vértices de la cónica tienen coordenadas

(- a, 0)

y

(a, 0)

, con

un valor

no negativo .

El eje semi mayor es el valor

a

.

El eje semi-menor es el valor

b

en la ecuación cartesiana estándar de la elipse o hipérbola.

Las siguientes relaciones tienen:

$pe = \ ell \,$
$ae = c. \,$

Estos parámetros están relacionados como se muestra en la siguiente tabla, donde se supone la posición estándar. En todos los casos,

una

y

b

son positivos.

sección cónica	ecuación	excentricidad ( $e$ )	excentricidad lineal ( $c$ )	recto semi-latus ( $ℓ$ )	parámetro focal ( $p$ )
circulo	$x ^ {2} + y ^ {2} = a ^ {2} \,$	$0 \,$	$0 \,$	$un\,$	$\ infty$
elipse	${\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} = 1$	${\ sqrt {1 - {\ frac {b ^ {2}} {a ^ {2}}}}}$	${\ sqrt {a ^ {2} -b ^ {2}}}$	${\ frac {b ^ {2}} {a}}$	${\ frac {b ^ {2}} {\ sqrt {a ^ {2} -b ^ {2}}}}$
parábola	$y ^ {2} = 4ax \,$	$1 \,$	N / A	$2a \,$	$2a \,$
hipérbola	${\ frac {x ^ {2}} {a ^ {2}}} - {\ frac {y ^ {2}} {b ^ {2}}} = 1$	${\ sqrt {1 + {\ frac {b ^ {2}} {a ^ {2}}}}}$	${\ sqrt {a ^ {2} + b ^ {2}}}$	${\ frac {b ^ {2}} {a}}$	${\ frac {b ^ {2}} {\ sqrt {a ^ {2} + b ^ {2}}}}$

Formularios estándar en coordenadas cartesianas

Formas estándar de una elipse

Formas estándar de una parábola

Formas estándar de una hipérbola

Después de introducir coordenadas cartesianas, la propiedad focus-directrix se puede usar para producir ecuaciones que las coordenadas de los puntos de la sección cónica deben cumplir. Mediante un cambio de coordenadas (una rotación de ejes y una traslación de ejes) estas ecuaciones se pueden poner en formas estándar . Para las elipses y las hipérbolas (generales) una forma estándar tendría el eje

x

como el eje principal y el origen (el punto (0,0)) como el centro. Los vértices tendrían coordenadas

(\pm a, 0)

y coordenadas focales

(\pm c, 0)

. Defina

b

por las ecuaciones

c = a - b

para una elipse y

c = a + b

para una hipérbola. Para un círculo,

c = 0

entonces

a = b

. Para la parábola, la forma estándar tiene el foco en el eje

x

en el punto

(a, 0)

y la directriz en la línea con la ecuación

x = - a

. En forma estándar, la parábola siempre pasará por el origen. Un caso especial de hipérbola ocurre cuando sus asíntotas son perpendiculares. Este caso especial se llama hipérbolarectangular o equilátera . En este caso, la forma estándar se obtiene tomando las asíntotas como los ejes de coordenadas y la línea

x = y

como el eje principal. Los focos tendrían coordenadas

(c, c)

y

(- c, - c)

.

Círculo: $x + y = a$
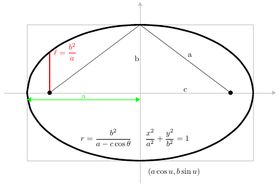
Elipse: $x / a + y / b = 1$
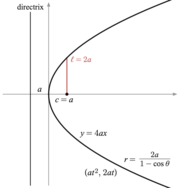
Parábola: $y = 4 hacha$ con $a > 0$
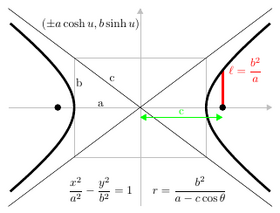
Hiperbola: $x / a - y / b = 1$
Hipérbola rectangular: $xy = c / 2$

Los primeros cuatro de estas formas son simétricas alrededor de tanto la

x

eje x y

y

eje x (por el círculo, elipse y la hipérbola), o acerca de la

x

eje x solamente (para la parábola). La hipérbola rectangular, sin embargo, es en cambio simétrico alrededor de las líneas

Y = x

y

y = - x

.

Estas formas estándar se pueden escribir paramétricamente como,

Circle: $(a cos θ, a sin θ)$ ,
Elipse: $(a cos θ, b sin θ)$ ,
Parábola: $(at, 2 at)$ ,
Hiperbola: $(un sec θ, b tan θ)$ o $(\pm a cosh u, b sinh u)$ ,
Hipérbola rectangular: donde ${\ displaystyle (dt, {\ frac {d} {t}})}$ ${\ displaystyle d = {\ frac {c} {\ sqrt {2}}}.}$

Forma cartesiana general

En el sistema de coordenadas cartesianas, el gráfico de una ecuación cuadrática en dos variables es siempre una sección cónica (aunque puede ser degenerada), y todas las secciones cónicas surgen de esta manera. La ecuación más general es de la forma

{\ displaystyle Ax ^ {2} + Bxy + Cy ^ {2} + Dx + Ey + F = 0,}

con todos los coeficientes, los números reales y

A, B, C

no son todos cero.

Notación de matriz

La ecuación anterior se puede escribir en notación de matriz como

{\ displaystyle \ left ({\ begin {matrix} x & y \ end {matrix}} \ right) \ left ({\ begin {matrix} A & B / 2 \\ B / 2 & C \ end {matrix}} \ right) \ left ({\ begin {matrix} x \\ y \ end {matrix}} \ right) + \ left ({\ begin {matrix} D & E \ end {matrix}} \ right) \ left ({\ begin {matriz} x \\ y \ end {matrix}} \ right) + F = 0.}

La ecuación general también se puede escribir como

{\ displaystyle \ left ({\ begin {matrix} x & y & 1 \ end {matrix}} \ right) \ left ({\ begin {matrix} A & B / 2 & D / 2 \\ B / 2 & C & E / 2 \\ D / 2 & E / 2 & F \ end {matrix}} \ right) \ left ({\ begin {matrix} x \\ y \\ 1 \ end {matrix}} \ right) = 0.}

Esta forma es una especialización de la forma homogénea utilizada en el entorno más general de la geometría proyectiva (ver más abajo).

Discriminante

Las secciones cónicas descritas por esta ecuación se pueden clasificar en términos del valor , llamado el discriminante de la ecuación. Por lo tanto, el discriminante es

- 4Δ

donde

Δ

es el determinante de la matriz

B ^ {2} -4AC

{\ displaystyle \ left | {\ begin {matrix} A & B / 2 \\ B / 2 & C \ end {matrix}} \ right |.}

Si la cónica no es degenerada, entonces:

si B - 4 AC <0 , la ecuación representa una elipse;
- si $A = C$ y $B = 0$ , la ecuación representa un círculo, que es un caso especial de una elipse;
si $B - 4 AC = 0$ , la ecuación representa una parábola;
si B - 4 AC > 0 , la ecuación representa una hipérbola;
- si $A + C = 0$ , la ecuación representa una hipérbola rectangular.

En la notación utilizada aquí,

A

y

B

son coeficientes del polinomio, en contraste con algunas fuentes que denotan los semiejes mayor y menor como

A

y

B

.

Invariantes

El discriminante

B - 4 AC

de la ecuación cuadrática de la sección cónica (o equivalente al determinante

AC - B / 4

de la matriz 2 × 2) y la cantidad

A + C

(el rastro de la matriz 2 × 2) son invariantes bajo rotaciones arbitrarias y traducciones de los ejes de coordenadas, como es el determinante de la matriz 3 × 3 anterior. El término constante

F

y la suma

D + E

son invariantes solo bajo rotación.

Excentricidad en términos de coeficientes

Cuando la sección cónica está escrita algebraicamente como

Ax ^ {2} + Bxy + Cy ^ {2} + Dx + Ey + F = 0, \,

la excentricidad se puede escribir como una función de los coeficientes de la ecuación cuadrática. Si

4 AC = B

la cónica es una parábola y su excentricidad es igual a 1 (siempre que no sea degenerada). De lo contrario, suponiendo que la ecuación representa una hipérbola o elipse no degenerada, la excentricidad está dada por

e = {\ sqrt {\ frac {2 {\ sqrt {(AC) ^ {2} + B ^ {2}}}} {\ eta (A + C) + {\ sqrt {(AC) ^ {2} + B ^ {2}}}}}},

donde

η = 1

si el determinante de la matriz de 3 × 3 de arriba es negativo y

η = -1

si ese determinante es positivo.

También se puede demostrar que la excentricidad es una solución positiva de la ecuación

{\ displaystyle \ Delta e ^ {4} + [(A + C) ^ {2} -4 \ Delta] e ^ {2} - [(A + C) ^ {2} -4 \ Delta] = 0, }

donde otra vez Esto tiene precisamente una solución positiva -la excentricidad- en el caso de una parábola o elipse, mientras que en el caso de una hipérbola tiene dos soluciones positivas, una de las cuales es la excentricidad.

{\ displaystyle \ Delta = AC - {\ frac {B ^ {2}} {4}}.}

Conversión a forma canónica

En el caso de una elipse o hipérbola, la ecuación

{\ displaystyle Ax ^ {2} + Bxy + Cy ^ {2} + Dx + Ey + F = 0 \,}

se puede convertir a la forma canónica en variables transformadas como

{\ displaystyle x ', y'}

{\ displaystyle {\ frac {x '^ {2}} {- S / (\ lambda _ {1} ^ {2} \ lambda _ {2})}} + {\ frac {y' ^ {2}} {-S / (\ lambda _ {1} \ lambda _ {2} ^ {2})}} = 1,}

o equivalente

{\ displaystyle {\ frac {x '^ {2}} {- S / (\ lambda _ {1} \ Delta)}} + {\ frac {y' ^ {2}} {- S / (\ lambda _ {2} \ Delta)}} = 1,}

donde y son los valores propios de la matriz , es decir, las soluciones de la ecuación

\ lambda _ {1}

\ lambda _ {2}

{\ displaystyle \ left ({\ begin {matrix} A & B / 2 \\ B / 2 & C \ end {matrix}} \ right)}

{\ displaystyle \ lambda ^ {2} - (A + C) \ lambda + (AC- (B / 2) ^ {2}) = 0}

- y es el determinante de la matriz 3 × 3 anterior, y es de nuevo el determinante de la matriz 2 × 2. En el caso de una elipse, los cuadrados de los dos semiejes están dados por los denominadores en forma canónica.

S

\ Delta = \ lambda _ {1} \ lambda _ {2}

Coordenadas polares

Desarrollo de la sección cónica a medida que la excentricidad e aumenta

En coordenadas polares, una ecuación de cónica con un foco en el origen y, en su caso, el otro en un valor negativo (para una elipse) o un valor positivo (para una hipérbola) en el eje

x

, viene dada por la ecuación

r = {\ frac {l} {1 + e \ cos \ theta}},

donde

e

es la excentricidad

yl

es el recto semi-latus.

Como arriba, para

e = 0

, el gráfico es un círculo, para

0 < e <1

el gráfico es una elipse, para

e = 1

una parábola, y para

e > 1 es

una hipérbola.

La forma polar de la ecuación de una cónica se usa a menudo en dinámica; por ejemplo, determinar las órbitas de los objetos que giran alrededor del Sol.

Propiedades

Así como dos puntos (distintos) determinan una línea, cinco puntos determinan una cónica. Formalmente, dados cinco puntos en el plano en posición lineal general, lo que significa que no hay tres colineales, hay un paso cónico único que pasa a través de ellos, que no será degenerado; esto es cierto tanto en el plano euclidiano como en su extensión, el plano proyectivo real. De hecho, dados cinco puntos, hay una cónica que los atraviesa, pero si tres de los puntos son colineales, la cónica será degenerada (reducible, porque contiene una línea) y puede que no sea única; ver más discusión.

Cuatro puntos en el plano en posición lineal general determinan un paso cónico único a través de los primeros tres puntos y teniendo el cuarto punto como su centro. Por lo tanto, conocer el centro equivale a conocer dos puntos en la cónica con el propósito de determinar la curva.

Además, una cónica está determinada por cualquier combinación de k puntos en la posición general que atraviesa y 5 - k líneas que son tangentes a ella, para 0≤ k ≤5.

Cualquier punto en el plano está en cero, una o dos líneas tangentes de una cónica. Un punto en una sola línea tangente está en la cónica. Se dice que un punto en una línea no tangente es un punto interior (o punto interno ) de la cónica, mientras que un punto en dos líneas tangentes es un punto exterior (o punto exterior ).

Todas las secciones cónicas comparten una propiedad de reflexión que se puede expresar como: Todos los espejos en forma de sección cónica no degenerada reflejan la luz que proviene de un foco o se dirige hacia uno o hacia el otro foco. En el caso de la parábola, el segundo foco debe considerarse como infinitamente lejano, de modo que los rayos de luz que van hacia o desde el segundo foco son paralelos.

El teorema de Pascal se refiere a la colinealidad de tres puntos que se construyen a partir de un conjunto de seis puntos en cualquier cónica no degenerada. El teorema también se aplica a las cónicas degeneradas que constan de dos líneas, pero en ese caso se conoce como el teorema de Pappus.

Las secciones cónicas no degeneradas son siempre "suaves". Esto es importante para muchas aplicaciones, como la aerodinámica, donde se requiere una superficie lisa para garantizar el flujo laminar y evitar las turbulencias.

Historia

Menaechmus y primeros trabajos

Se cree que la primera definición de una sección cónica se debe a Menaechmus (murió 320 a. C.) como parte de su solución del problema de Delia (duplicación del cubo). Su trabajo no sobrevivió, ni siquiera los nombres que usó para estas curvas, y solo se conoce a través de cuentas secundarias. La definición utilizada en ese momento difiere de la utilizada comúnmente en la actualidad. Los conos se construyeron girando un triángulo rectángulo alrededor de una de sus patas para que la hipotenusa genere la superficie del cono (dicha línea se llama generatriz). Se determinaron tres tipos de conos por sus ángulos de vértice (medidos por el doble del ángulo formado por la hipotenusa y la pierna rotando en el triángulo rectángulo). La sección cónica se determinó mediante la intersección de uno de estos conos con un plano dibujado perpendicularmente a una generatriz. El tipo de cono se determina por el tipo de cono, es decir, por el ángulo formado en el vértice del cono: si el ángulo es agudo, entonces el cono es una elipse; si el ángulo es correcto, entonces la cónica es una parábola; y si el ángulo es obtuso, la cónica es una hipérbola (pero solo una rama de la curva).

Se dice que Euclid (aproximadamente 300 aC) escribió cuatro libros sobre cónicas, pero también se perdieron. Se sabe que Arquímedes (fallecido hacia el 212 aC) estudió las cónicas, y determinó el área delimitada por una parábola y un acorde en la cuadratura de la parábola . Su principal interés fue en términos de medición de áreas y volúmenes de figuras relacionadas con las cónicas y parte de este trabajo sobrevive en su libro sobre los sólidos de la revolución de las cónicas, On Conoids y Spheroids .

Apolonio de Perga

Diagrama de Cónicas de Apolonio , en una traducción al árabe del siglo IX

El mayor progreso en el estudio de las cónicas por parte de los antiguos griegos se debe a Apolonio de Perga (fallecido en 190 aC), cuyas secciones cónicas de ocho volúmenes o Cónicas resumieron y ampliaron enormemente el conocimiento existente. El estudio de Apolonio de las propiedades de estas curvas permitió mostrar que cualquier plano que corte un cono doble fijo (dos siestas), independientemente de su ángulo, producirá una cónica de acuerdo con la definición anterior, lo que lleva a la definición comúnmente utilizada en la actualidad. Círculos, no construibles por el método anterior, también se pueden obtener de esta manera. Esto puede explicar por qué Apolonio consideraba que los círculos eran un cuarto tipo de sección cónica, una distinción que ya no se hace. Apolonio usó los nombres elipse , parábola y hipérbola para estas curvas, tomando prestada la terminología del trabajo de Pitágoras anterior en áreas.

A Pappus de Alejandría (fallecido hacia el año 350 dC) se le atribuye la importancia del concepto de foco cónico y el concepto relacionado de una directriz, incluido el caso de la parábola (que falta en las obras conocidas de Apolonio).

Al-Kuhi

Un instrumento para dibujar secciones cónicas fue descrito por primera vez en el año 1000 EC por el matemático islámico Al-Kuhi.

Omar Khayyám

El trabajo de Apolonio fue traducido al árabe y gran parte de su trabajo solo sobrevive a través de la versión árabe. Persas encontraron aplicaciones a la teoría; el más notable de ellos fue el matemático y poeta persa Omar Khayyám quien usó secciones cónicas para resolver ecuaciones algebraicas.

Europa

Johannes Kepler amplió la teoría de las cónicas a través del "principio de continuidad", un precursor del concepto de límites. Kepler utilizó por primera vez el término focos en 1604.

Girard Desargues y Blaise Pascal desarrollaron una teoría de las cónicas usando una forma temprana de geometría proyectiva y esto ayudó a impulsar el estudio de este nuevo campo. En particular, Pascal descubrió un teorema conocido como hexagrammum mysticum del cual pueden deducirse muchas otras propiedades de las cónicas.

René Descartes y Pierre Fermat aplicaron su geometría analítica recién descubierta al estudio de las cónicas. Esto tuvo el efecto de reducir los problemas geométricos de las cónicas a problemas en álgebra. Sin embargo, fue John Wallis en su tratado de 1655 Tractatus de sectionibus conicis quien primero definió las secciones cónicas como ejemplos de ecuaciones de segundo grado. Escrita antes, pero publicada más tarde, Elementa Curvarum Linearum de Jan de Witt comienza con la construcción cinemática de las cónicas de Kepler y luego desarrolla las ecuaciones algebraicas. Este trabajo, que utiliza la metodología de Fermat y la notación de Descartes ha sido descrito como el primer libro de texto sobre el tema. De Witt inventó el término directriz .

Aplicaciones

La forma paraboloide de Archeocyathids produce secciones cónicas en las rocas

Las secciones cónicas son importantes en astronomía: las órbitas de dos objetos masivos que interactúan de acuerdo con la ley de gravitación universal de Newton son secciones cónicas si se considera que su centro de masa común está en reposo. Si están unidos, ambos trazarán elipsis; si se están separando, ambos seguirán parábolas o hipérbolas. Ver problema de dos cuerpos.

Las propiedades reflectantes de las secciones cónicas se utilizan en el diseño de reflectores, radiotelescopios y algunos telescopios ópticos. Un espejo parabólico se utiliza como reflector, con una bombilla en el foco, en un reflector. El telescopio óptico Herschel de 4,2 metros en La Palma, en las Islas Canarias, utiliza un espejo parabólico primario para reflejar la luz hacia un espejo hiperbólico secundario, que lo refleja de nuevo en un foco detrás del primer espejo.

En el plano proyectivo real

Las secciones cónicas tienen algunas propiedades muy similares en el plano euclidiano y las razones para esto se vuelven más claras cuando las cónicas se ven desde la perspectiva de una geometría más grande. El plano euclidiano puede estar incrustado en el plano proyectivo real y las cónicas se pueden considerar como objetos en esta geometría proyectiva. Una forma de hacerlo es introducir coordenadas homogéneas y definir una cónica como el conjunto de puntos cuyas coordenadas satisfacen una ecuación cuadrática irreductible en tres variables (o equivalentemente, los ceros de una forma cuadrática irreductible). Más técnicamente, el conjunto de puntos que son ceros de una forma cuadrática (en cualquier número de variables) se denomina cuadrícula, y los cuadrículos irreducibles en un espacio proyectivo bidimensional (es decir, que tienen tres variables) se denominan tradicionalmente cónicas.

El plano Euclidiano

R

está incrustado en el plano proyectivo real colindando una línea en el infinito (y sus puntos correspondientes en el infinito) de modo que todas las líneas de una clase paralela se encuentran en esta línea. Por otro lado, comenzando con el plano proyectivo real, se obtiene un plano euclidiano distinguiendo alguna línea como la línea en el infinito y quitándola y todos sus puntos.

Intersección en el infinito

En un espacio proyectivo sobre cualquier anillo de división, pero en particular sobre los números reales o complejos, todas las cónicas no degeneradas son equivalentes, y por lo tanto en la geometría proyectiva uno simplemente habla de "una cónica" sin especificar un tipo. Es decir, hay una transformación proyectiva que correlacionará cualquier cónica no degenerada con cualquier otra cónica no degenerada.

Los tres tipos de secciones cónicas reaparecerán en el plano afín obtenido eligiendo una línea del espacio proyectivo para ser la línea en el infinito. Los tres tipos están determinados por cómo esta línea en el infinito se cruza con la cónica en el espacio proyectivo. En el espacio afín correspondiente, se obtiene una elipse si la cónica no se cruza con la línea en infinito, una parábola si la cónica intersecta la línea en infinito en un punto doble correspondiente al eje, y una hipérbola si la cónica corta la línea en infinito en dos puntos correspondientes a las asíntotas.

Coordenadas homogéneas

En coordenadas homogéneas, una sección cónica se puede representar como:

{\ displaystyle Ax ^ {2} + Bxy + Cy ^ {2} + Dxz + Eyz + Fz ^ {2} = 0.}

O en notación de matriz

{\ displaystyle \ left ({\ begin {matrix} x & y & z \ end {matrix}} \ right) \ left ({\ begin {matrix} A & B / 2 & D / 2 \\ B / 2 & C & E / 2 \\ D / 2 & E / 2 & F \ end {matrix}} \ right) \ left ({\ begin {matrix} x \\ y \\ z \ end {matrix}} \ right) = 0.}

La matriz de 3 × 3 de arriba se llama matriz de la sección cónica .

Algunos autores prefieren escribir la ecuación general homogénea como

{\ displaystyle Ax ^ {2} + 2Bxy + Cy ^ {2} + 2Dxz + 2Eyz + Fz ^ {2} = 0,}

(o alguna variación de esto) para que la matriz de la sección cónica tenga la forma más simple,

{\ displaystyle M = \ left ({\ begin {matrix} A & B & D \\ B & C & E \\ D & E & F \ end {matrix}} \ right),}

pero esta notación no se usa en este artículo.

Si el determinante de la matriz de la sección cónica es cero, la sección cónica está degenerada.

Como al multiplicar los seis coeficientes por el mismo escalar distinto de cero se obtiene una ecuación con el mismo conjunto de ceros, se pueden considerar las cónicas, representadas por

(A, B, C, D, E, F)

como puntos en el proyectivo de cinco dimensiones espacio

\ mathbf {P} ^ {5}.

Definición proyectiva de un círculo

Los conceptos métricos de la geometría euclidiana (conceptos relacionados con la medición de longitudes y ángulos) no pueden extenderse inmediatamente al plano proyectivo real. Deben redefinirse (y generalizarse) en esta nueva geometría. Esto se puede hacer para planos proyectivos arbitrarios, pero para obtener el plano proyectivo real como el plano euclidiano extendido, deben hacerse algunas elecciones específicas.

Repare una línea arbitraria en un plano descriptivo que se denominará línea absoluta . Seleccione dos puntos distintos en la línea absoluta y consúltelos como puntos absolutos . Se pueden definir varios conceptos métricos con referencia a estas elecciones. Por ejemplo, dada una línea que contiene los puntos

A

y

B

, el punto medio de segmento de línea

AB

se define como el punto

C

, que es el conjugado armónico proyectiva del punto de intersección de

AB

y la línea absoluta, con respecto a

A

y

B

.

Una cónica en un plano proyectivo que contiene los dos puntos absolutos se llama círculo . Como cinco puntos determinan una cónica, un círculo (que puede estar degenerado) está determinado por tres puntos. Para obtener el plano euclidiano extendido, la línea absoluta se elige como la línea en el infinito del plano euclidiano y los puntos absolutos son dos puntos especiales en esa línea llamados puntos circulares en el infinito. Las líneas que contienen dos puntos con coordenadas reales no pasan por los puntos circulares en el infinito, por lo que en el plano euclidiano un círculo, bajo esta definición, está determinado por tres puntos que no son colineales.

Se ha mencionado que los círculos en el plano euclidiano no se pueden definir mediante la propiedad focus-directrix. Sin embargo, si uno considerara la línea en el infinito como la directriz, entonces al tomar la excentricidad como

e = 0,

un círculo tendrá la propiedad focus-directrix, pero aún no está definida por esa propiedad. Hay que tener cuidado en esta situación para usar correctamente la definición de excentricidad como la razón de la distancia de un punto en el círculo al foco (longitud de un radio) a la distancia de ese punto a la directriz (esta distancia es infinita) que da el valor límite de cero.

Definición cónica proyectiva de Steiner

Definición de la generación Steiner de una sección cónica

Un enfoque sintético (sin el uso de coordenadas) para definir las secciones cónicas en un plano proyectivo fue proporcionado por Jakob Steiner en 1867.

Dado dos lápices de líneas en dos puntos (todas las líneas que contienen y resp.) Y un mapeo proyectivo pero no perspectiva de a . Luego, los puntos de intersección de las líneas correspondientes forman una sección cónica proyectiva no degenerada. $B (U), B (V)$ $U, V$ $U$ $V$ $\Pi$ $B (U)$ $B (V)$

Un mapeo en perspectiva de un lápiz sobre un lápiz es una biyección (correspondencia de 1-1) tal que las líneas correspondientes se cruzan en una línea fija , que se llama el eje de la perspectiva .

\Pi

B (U)

B (V)

un

\Pi

Un mapeo proyectivo es una secuencia finita de mapeos de perspectiva.

Como un mapeo proyectivo en un plano proyectivo sobre un campo (plano pappiano) se determina de manera única prescribiendo las imágenes de tres líneas, para la generación Steiner de una sección cónica, además de dos puntos solo se deben dar las imágenes de 3 líneas. Estos 5 elementos (2 puntos, 3 líneas) determinan de manera única la sección cónica.

U, V

Line conics

Por el Principio de Dualidad en un plano proyectivo, el dual de cada punto es una línea, y el dual de un locus de puntos (un conjunto de puntos que satisfacen alguna condición) se llama una envolvente de líneas. Utilizando la definición de Steiner de una cónica (este locus de puntos se denominará ahora punto cónico ) como el encuentro de los rayos correspondientes de dos lápices relacionados, es fácil dualizar y obtener la envolvente correspondiente que consiste en las uniones de puntos correspondientes de dos rangos relacionados (puntos en una línea) en diferentes bases (las líneas en las que están los puntos). Tal sobre se llama una línea cónica (o doble cónica ).

En el plano proyectivo real, un punto cónico tiene la propiedad de que cada línea lo encuentra en dos puntos (que pueden coincidir, o pueden ser complejos) y cualquier conjunto de puntos con esta propiedad es un punto cónico. Se sigue dualmente que una línea cónica tiene dos de sus líneas a través de cada punto y cualquier envolvente de líneas con esta propiedad es una línea cónica. En cada punto de un punto cónico hay una línea tangente única, y dualmente, en cada línea de una línea cónica hay un punto único llamado punto de contacto . Un teorema importante establece que las líneas tangentes de un punto cónico forman una línea cónica, y dualmente, los puntos de contacto de una línea cónica forman un punto cónico.

La definición de Von Staudt

Karl Georg Christian von Staudt definió una cónica como el conjunto de puntos dado por todos los puntos absolutos de una polaridad que tiene puntos absolutos. Von Staudt introdujo esta definición en Geometrie der Lage (1847) como parte de su intento de eliminar todos los conceptos métricos de la geometría proyectiva.

Una polaridad ,

π

, de un plano proyectivo,

P

, es una biyección involutoria (es decir, de orden dos) entre los puntos y las líneas de

P

que preserva la relación de incidencia. Por lo tanto, una polaridad relaciona un punto

Q

con una línea

qy

, siguiendo a Gergonne,

q

se llama polar de

Q

y

Q

el polo de

q

. Un punto ( línea ) absoluto de una polaridad es uno que incide con su polar (polo).

Una cónica de von Staudt en el plano proyectivo real es equivalente a una cónica Steiner.

Construcciones

Una cónica no se puede construir como una curva continua (o dos) con regla y compás. Sin embargo, hay varios métodos que se utilizan para construir tantos puntos individuales en una cónica, con regla y brújula, según se desee.

Una de ellas se basa en el inverso del teorema de Pascal, es decir, si los puntos de intersección de los lados opuestos de un hexágono son colineales, entonces los seis vértices se encuentran en una cónica. Específicamente, dados cinco puntos,

A, B, C, D, E

y una línea que pasa por

E

, digamos

EG

, se puede construir un punto

F

que se encuentra en esta línea y está en la cónica determinada por los cinco puntos. Deje que

AB se

encuentre con

DE

en

L

,

BC

con

EG

en

M

y deje que

CD se

reúnan

LM

en

N

. Entonces

AN

cumple con

EG

en el punto requerido

F

. Al variar la línea a través de

E

, se pueden construir tantos puntos adicionales en la cónica como se desee.

Método de paralelogramo para construir una elipse

Otro método, basado en la construcción de Steiner y que es útil en aplicaciones de ingeniería, es el método de paralelogramo , donde una cónica se construye punto por punto mediante la conexión de ciertos puntos igualmente espaciados en una línea horizontal y una línea vertical. Específicamente, para construir la elipse con la ecuación

x / a + y / b = 1

, construya primero el rectángulo

ABCD

con los vértices

A (a, 0), B (a, 2 b), C (- a, 2 b)

y

D (- a, 0)

. Divida el lado

BC

en

n

segmentos iguales y use una proyección paralela, con respecto a la diagonal

AC

, para formar segmentos iguales en el lado

AB

(las longitudes de estos segmentos serán

b / a por

la longitud de los segmentos en

BC

). En el lado

BC

etiqueta los puntos extremos izquierdos de los segmentos con

A 1

a

A n

a partir de

B

y va hacia

C

. En el lado

AB,

etiquete los puntos finales superiores

D 1

a

D n

a partir de

A

y yendo hacia

B

. Los puntos de intersección,

AA i \cap DD i

para

1 \leq i \leq n

serán puntos de la elipse entre

A

y

P (0, b)

. El etiquetado asocia las líneas del lápiz a través de

A

con las líneas del lápiz a través de

D, de forma

proyectiva pero no de forma perspectiva. La cónica buscada se obtiene por esta construcción desde tres puntos

A, D

y

P

y dos tangentes (las líneas verticales en

A

y

D

) determinar de forma única la cónica. Si se usa otro diámetro (y su diámetro conjugado) en lugar de los ejes mayor y menor de la elipse, se usa un paralelogramo que no es un rectángulo en la construcción, dando el nombre del método. La asociación de líneas de los lápices se puede extender para obtener otros puntos en la elipse. Las construcciones para hipérbolas y parábolas son similares.

Otro método más general utiliza la propiedad de polaridad para construir la envolvente tangente de una cónica (una línea cónica).

En el complejo plano proyectivo

Es posible una mayor unificación si se permiten números complejos como coeficientes. En el plano proyectivo complejo, las cónicas no degeneradas no pueden distinguirse entre sí.

Sobre los números complejos, las elipses y las hipérbolas no son distintas, ya que -1 es un cuadrado; precisamente, la elipse se convierte en una hipérbola bajo la sustitución geométricamente una rotación compleja, cede - una hipérbola es simplemente una elipse con una longitud de eje imaginario. Por lo tanto, hay una clasificación bidireccional: elipse / hipérbola y parábola. Geométricamente, esto corresponde a la intersección de la línea en infinito en 2 puntos distintos (correspondientes a dos asíntotas) o en 1 punto doble (que corresponde al eje de una parábola), y así la hipérbola real es una imagen más sugerente para la elipse compleja / hipérbola, ya que también tiene 2 intersecciones (reales) con la línea en el infinito.

x ^ {2} + y ^ {2} = 1

y = iw,

x ^ {2} -w ^ {2} = 1

Se puede demostrar que en el plano proyectivo complejo CP dos secciones cónicas tienen cuatro puntos en común (si se tiene en cuenta la multiplicidad), por lo que nunca hay más de 4 puntos de intersección y siempre hay un punto de intersección (posibilidades: cuatro puntos de intersección distintos , dos puntos de intersección singulares y un punto de intersección doble, dos puntos de intersección doble, un punto de intersección singular y 1 con multiplicidad 3, 1 punto de intersección con multiplicidad 4). Si existe al menos un punto de intersección con multiplicidad> 1, entonces se dice que las dos secciones cónicas son tangentes. Si solo hay un punto de intersección, que tiene multiplicidad 4, se dice que las dos secciones cónicas están circulando.

Además, cada línea recta cruza cada sección cónica dos veces. Si el punto de intersección es doble, se dice que la línea es tangente y se llama línea tangente. Debido a que cada línea recta se cruza con una sección cónica dos veces, cada sección cónica tiene dos puntos en el infinito (los puntos de intersección con la línea en el infinito). Si estos puntos son reales, la sección cónica es una hipérbola, si son imaginarios conjugados, la sección cónica es una elipse, si la sección cónica tiene un punto doble en el infinito, es una parábola. Si los puntos en el infinito son (1, i, 0) y (1, -i, 0), la sección cónica es un círculo (ver puntos circulares en el infinito). Si una sección cónica tiene un punto real y uno imaginario en el infinito, o dos puntos imaginarios que no están conjugados, entonces no es una sección cónica real, porque sus coeficientes no pueden ser reales.

Casos degenerados

Lo que debería considerarse como un caso degenerado de una cónica depende de la definición que se utiliza y la configuración geométrica de la sección cónica. Hay algunos autores que definen una cónica como cuadrícula no degenerada bidimensional. Con esta terminología no hay cónicas degeneradas (solo cuadrículas degeneradas), pero utilizaremos la terminología más tradicional y evitaremos esa definición.

En el plano euclidiano, usando la definición geométrica, un caso degenerado surge cuando el plano de corte pasa a través del vértice del cono. La cónica degenerada es: un punto, cuando el plano se cruza con el cono solo en el ápice; una línea recta, cuando el avión es tangente al cono (contiene exactamente un generador del cono); o un par de líneas que se intersectan (dos generadores del cono). Estos corresponden respectivamente a las formas limitantes de una elipse, parábola y una hipérbola.

Si una cónica en el plano euclidiano está siendo definida por los ceros de una ecuación cuadrática (es decir, como cuadrícula), entonces las cónicas degeneradas son: el conjunto vacío, un punto o un par de líneas que pueden ser paralelas, se cruzan en un punto, o coinciden. El caso de conjunto vacío puede corresponder ya sea a un par de líneas paralelas complejas conjugadas como con la ecuación o a una elipse imaginaria , como con la ecuación Una elipse imaginaria no satisface la definición general de degeneración, y por lo tanto no se considera normalmente como degenerado El caso de dos líneas se produce cuando la expresión cuadrática tiene en cuenta dos factores lineales, los ceros de cada uno dan una línea. En el caso de que los factores sean los mismos, las líneas correspondientes coinciden y nos referimos a la línea como un doble

{\ displaystyle x ^ {2} + 1 = 0,}

{\ displaystyle x ^ {2} + y ^ {2} + 1 = 0.}

línea (una línea con multiplicidad 2) y este es el caso anterior de un plano de corte tangente.

En el plano proyectivo real, dado que las líneas paralelas se encuentran en un punto de la línea en el infinito, el caso de línea paralelo del plano euclidiano se puede ver como líneas que se intersectan. Sin embargo, como el punto de intersección es el vértice del cono, el cono mismo se degenera en un cilindro, es decir, con el vértice en el infinito. Otras secciones en este caso se llaman secciones cilíndricas . Las secciones cilíndricas no degeneradas son elipses (o círculos).

Cuando se ven desde la perspectiva del plano proyectivo complejo, los casos degenerados de una cuadrícula real (es decir, la ecuación cuadrática tiene coeficientes reales) se pueden considerar como un par de líneas, posiblemente coincidentes. El conjunto vacío puede ser la línea en el infinito considerada como una línea doble, un punto (real) es la intersección de dos líneas conjugadas complejas y los otros casos como se mencionó anteriormente.

Para distinguir los casos degenerados de los no degenerados (incluido el conjunto vacío con el último) usando la notación de matriz, sea

β

el determinante de la matriz 3 × 3 de la sección cónica, es decir,

β = (AC - B / 4) F + BED - CD - AE / 4

; y deje que

α = B - 4 AC

sea el discriminante. Entonces la sección cónica no es degenerada si y solo si

β \neq 0

. Si

β = 0

tenemos un punto cuando

α <0

, dos líneas paralelas (posiblemente coincidentes) cuando

α = 0

, o dos líneas que se intersectan cuando

α > 0

.

Lápiz de cónicas

Una cónica (no degenerada) está completamente determinada por cinco puntos en posición general (no tres colineales) en un plano y el sistema de cónicas que pasa a través de un conjunto fijo de cuatro puntos (de nuevo en un plano y no tres colineales) se llama un lápiz de cónicas . Los cuatro puntos comunes se llaman puntos base del lápiz. A través de cualquier punto que no sea un punto base, pasa una sola cónica del lápiz. Este concepto generaliza un lápiz de círculos.

En un plano proyectivo definido sobre un campo algebraicamente cerrado, dos cónicas se juntan en cuatro puntos (contados con multiplicidad) y entonces, determina el lápiz de cónicas basado en estos cuatro puntos. Además, los cuatro puntos base determinan tres pares de líneas (cónicos degenerados a través de los puntos base, cada línea del par que contiene exactamente dos puntos base) y, por lo tanto, cada lápiz de cónicas contendrá como máximo tres cónicas degeneradas.

Un lápiz de cónicas puede representarse algebraicamente de la siguiente manera. Deje que

C 1

y

C 2

sean dos cónicas distintas en un plano proyectivo definido sobre un campo

K

algebraicamente cerrado . Para cada par

λ, μ

de elementos de

K

, no ambos cero, la expresión:

\ lambda C_ {1} + \ mu C_ {2}

representa una cónica en el lápiz determinada por

C 1

y

C 2

. Esta representación simbólica se puede concretar con un ligero abuso de la notación (usando la misma notación para denotar el objeto y la ecuación que define el objeto). Pensando en

C 1

, por ejemplo, como una forma cuadrática ternaria, entonces

C 1 = 0

es la ecuación de "cónica

C 1

". Otra realización concreta se obtendría pensando en

C 1

como la matriz simétrica 3 × 3 que lo representa. Si

C 1

y

C 2

tener tales realizaciones concretas entonces cada miembro del lápiz anterior también lo hará. Como la configuración usa coordenadas homogéneas en un plano proyectivo, dos representaciones concretas (ya sean ecuaciones o matrices) dan la misma cónica si difieren en una constante multiplicativa distinta de cero.

Intersección de dos cónicas

Las soluciones a un sistema de dos ecuaciones de segundo grado en dos variables se pueden ver como las coordenadas de los puntos de intersección de dos secciones cónicas genéricas. En particular, dos cónicas pueden poseer ninguno, dos o cuatro puntos de intersección posiblemente coincidentes. Un método eficiente para localizar estas soluciones explota la representación homogénea de la matriz de secciones cónicas, es decir, una matriz simétrica 3x3 que depende de seis parámetros.

El procedimiento para ubicar los puntos de intersección sigue estos pasos, donde las cónicas están representadas por matrices:

dadas las dos cónicas y , considere el lápiz de cónicas dado por su combinación lineal $C_ {1}$ $C_ {2}$ $\ lambda C_ {1} + \ mu C_ {2}.$
identifica los parámetros homogéneos que corresponden a la cónica degenerada del lápiz. Esto se puede hacer imponiendo la condición y resolviendo para y . Estas resultan ser las soluciones de una ecuación de tercer grado. $(\ lambda, \ mu)$ $\ det (\ lambda C_ {1} + \ mu C_ {2}) = 0$ $\ lambda$ $\ mu$
dada la cónica degenerada , identifique las dos líneas, posiblemente coincidentes, que la constituyen. $C_ {0}$
interseque cada línea identificada con una de las dos cónicas originales; este paso se puede hacer de manera eficiente utilizando la representación cónica doble de $C_ {0}$
los puntos de intersección representarán las soluciones al sistema de ecuaciones inicial.

Generalizaciones

Las cónicas se pueden definir sobre otros campos (es decir, en otras geometrías pappianas). Sin embargo, se debe tener cierto cuidado cuando el campo tiene la característica 2, ya que algunas fórmulas no se pueden usar. Por ejemplo, las representaciones matriciales usadas anteriormente requieren división por 2.

Una generalización de una cónica no degenerada en un plano proyectivo es un óvalo. Un óvalo es un conjunto de puntos que tiene las siguientes propiedades, que son sostenidas por cónicas: 1) cualquier línea se cruza con un óvalo en ninguno, uno o dos puntos, 2) en cualquier punto del óvalo existe una línea tangente única.

Al generalizar las propiedades de enfoque de las cónicas para el caso en el que hay más de dos focos produce conjuntos llamados cónicos generalizados.

En otras áreas de las matemáticas

La clasificación en elíptica, parabólica e hiperbólica es omnipresente en las matemáticas, y a menudo divide un campo en subcampos claramente distintos. La clasificación surge principalmente debido a la presencia de una forma cuadrática (en dos variables esto corresponde al discriminante asociado), pero también puede corresponder a la excentricidad.

Clasificaciones de formas cuadráticas:

Formas cuadráticas

Las formas cuadráticas sobre los reales se clasifican por la ley de inercia de Sylvester, concretamente por su índice positivo, índice cero e índice negativo: una forma cuadrática en n variables se puede convertir a una forma diagonal, como donde el número de coeficientes +1, k , es el índice positivo, el número de -1 coeficientes, ℓ , es el índice negativo, y las variables restantes son el índice cero m, por lo tanto , en dos variables, las formas cuadráticas distintas de cero se clasifican como:

{\ displaystyle x_ {1} ^ {2} + x_ {2} ^ {2} + \ cdots + x_ {k} ^ {2} -x_ {k + 1} ^ {2} - \ cdots -x_ {k + \ ell} ^ {2},}

{\ displaystyle k + \ ell + m = n.}

$x ^ {2} + y ^ {2}$ - positivo-definido (el negativo también está incluido), que corresponde a las elipsis,
$x ^ {2}$ - degenerado, que corresponde a las parábolas, y
$x ^ {2} -y ^ {2}$ - indefinido, que corresponde a hipérbolas.

En dos variables, las formas cuadráticas se clasifican por discriminante, análogamente a las cónicas, pero en dimensiones más altas la clasificación más útil es definida, (todas positivas o totalmente negativas), degenerada, (algunos ceros) o indefinida (mezcla de positivos y negativos, pero sin ceros). Esta clasificación subyace a muchos de los siguientes.

Curvatura

La curvatura gaussiana de una superficie describe la geometría infinitesimal, y puede ser positiva en cada punto: geometría elíptica, geometría euclidiana cero (plana, parábola) o geometría hiperbólica negativa; infinitesimalmente, en segundo orden, la superficie se parece a la gráfica de (o 0), o . De hecho, mediante el teorema de uniformización, se puede tomar cada superficie como globalmente (en cada punto) positivamente curvada, plana o curvada negativamente. En dimensiones más altas, el tensor de curvatura de Riemann es un objeto más complicado, pero los colectores con curvatura seccional constante son objetos de estudio interesantes, y tienen propiedades sorprendentemente diferentes, como se discute en la curvatura de la sección.

x ^ {2} + y ^ {2},

x ^ {2}

x ^ {2} -y ^ {2}

PDE de segundo orden

Las ecuaciones en derivadas parciales (PDE) de segundo orden se clasifican en cada punto como elípticas, parabólicas o hiperbólicas, de acuerdo con lo que sus términos de segundo orden corresponden a una forma cuadrática elíptica, parabólica o hiperbólica. El comportamiento y la teoría de estos diferentes tipos de PDEs son sorprendentemente diferentes; ejemplos representativos es que la ecuación de Poisson es elíptica, la ecuación de calor es parabólica y la ecuación de onda es hiperbólica.

Las clasificaciones de excentricidad incluyen:

Transformaciones de Möbius: Las transformaciones de Möbius real (elementos de PSL 2 ( R ) o su cubierta doble, SL 2 ( R )) se clasifican como elípticas, parabólicas o hiperbólicas en consecuencia, ya que su mitad de traza es o refleja la clasificación por excentricidad. $0 \ leq | \ operatorname {tr} | / 2 <1,$ $| \ operatorname {tr} | / 2 = 1,$ $| \ operatorname {tr} | / 2> 1,$
Relación de varianza a media: La relación de varianza a media clasifica varias familias importantes de distribuciones de probabilidad discretas: la distribución constante como circular (excentricidad 0), las distribuciones binomiales como elípticas, las distribuciones de Poisson como parabólicas y las distribuciones binomiales negativas como hiperbólicas. Esto se elabora en cumulantes de algunas distribuciones de probabilidad discretas.

En este SVG interactivo, mueva hacia la izquierda y hacia la derecha sobre la imagen SVG para rotar el cono doble

Buscar en este blog

Wikiblog Cultulandia [es]

Sección cónica

Sección cónica

Definición

Geometría euclidiana

Definición

Excentricidad, enfoque y directriz

Parámetros cónicos

Formularios estándar en coordenadas cartesianas

Forma cartesiana general

Notación de matriz

Discriminante

Invariantes

Excentricidad en términos de coeficientes

Conversión a forma canónica

Coordenadas polares

Propiedades

Historia

Menaechmus y primeros trabajos

Apolonio de Perga

Al-Kuhi

Omar Khayyám

Europa

Aplicaciones

En el plano proyectivo real

Intersección en el infinito

Coordenadas homogéneas

Definición proyectiva de un círculo

Definición cónica proyectiva de Steiner

Line conics

La definición de Von Staudt

Construcciones

En el complejo plano proyectivo

Casos degenerados

Lápiz de cónicas

Intersección de dos cónicas

Generalizaciones

En otras áreas de las matemáticas

Contenidos Relacionados de Matemáticas ››