Wikiblog Cultulandia [es]

En matemáticas, un límite es el valor de una función (o secuencia) que "se aproxima" cuando la entrada (o índice) "se acerca" a algún valor. Los límites son esenciales para el cálculo (y el análisis matemático en general) y se usan para definir continuidad, derivadas e integrales.

El concepto de un límite de una secuencia se generaliza más al concepto de límite de una red topológica, y está estrechamente relacionado con el límite y el límite directo en la teoría de categorías.

En fórmulas, un límite generalmente se escribe como

\ lim _ {n \ to c} f (n) = L

y se lee como "el límite de

f

de

n

cuando

n se

acerca a

c

es igual a

L

". El hecho de que una función

f (n) se

acerque al límite

L

cuando

n se

acerca a

c a

veces se denota con una flecha hacia la derecha (→), como en

f (n) \ a L \.

Límite de una función

Cada vez que un punto

x

está dentro

delta

unidades de

c

,

f (x)

se encuentra dentro de

varepsilon

unidades de

L

.

Para todos

x > S

,

f (x)

se encuentra dentro de

ε

de

L

.

Supongamos que

f

es una función de valor real y

c

es un número real. Intuitivamente hablando, la expresión

\ lim _ {x \ to c} f (x) = L

significa que

f (x)

puede estar tan cerca de

L

como se desee haciendo que

x

esté lo suficientemente cerca de

c

. En ese caso, la ecuación anterior puede leerse como "el límite de

f

de

x

, cuando

x se

aproxima a

c

, es

L

".

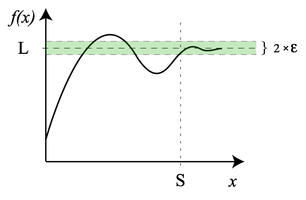
Augustin-Louis Cauchy en 1821, seguido de Karl Weierstrass, formalizó la definición del límite de una función que se conoció como la definición (ε, δ) de límite. La definición usa

ε

(la letra griega épsilon minúscula ) para representar cualquier pequeño número positivo, de modo que "

f (x) se

vuelve arbitrariamente cerca de

L

" significa que

f (x)

finalmente se encuentra en el intervalo

(L - ε, L + ε )

, que también se puede escribir usando el signo de valor absoluto como

| f (x) - L | <ε

. La frase "cuando

x se

aproxima a

c

" indica que nos referimos a valores de

x

cuya distancia de

c

es menor que algún número positivo

δ

(la letra griega minúscula delta ), es decir, valores de

x

dentro de cualquiera

(c - δ, c)

o

(c, c + δ)

, que se puede expresar con

0 <| x - c | <δ

. La primera desigualdad significa que la distancia entre

x

y

c

es mayor que

0

y eso

x \neq c

, mientras que el segundo indica que

x

está dentro de la distancia

δ

de

c

.

La anterior definición de un límite es cierto incluso si

f (c) \neq L

. De hecho, la función

f

no necesita ser definida en

c

.

Por ejemplo, si

f (x) = {\ frac {x ^ {2} -1} {x-1}}

entonces

f (1)

no está definido (ver división por cero), sin embargo, como

x se

mueve arbitrariamente cerca de 1,

f (x) se

aproxima a 2 en forma correspondiente:

f (0.9)	f (0.99)	f (0.999)	f (1.0)	f (1.001)	f (1.01)	f (1.1)
1.900	1.990	1.999	⇒ indefinido ⇐	2.001	2.010	2.100

Por lo tanto,

f (x)

se puede hacer arbitrariamente cerca del límite de 2 simplemente haciendo

x lo

suficientemente cerca de

1

.

En otras palabras,

\ lim _ {x \ to 1} {\ frac {x ^ {2} -1} {x-1}} = 2

Esto también se puede calcular algebraicamente, como para todos los números reales

x

\neq 1

.

{\ frac {x ^ {2} -1} {x-1}} = {\ frac {(x + 1) (x-1)} {x-1}} = x + 1

Ahora, dado que

x + 1

es continuo en

x

en 1, ahora podemos conectar 1 para

x

, por lo tanto .

\ lim _ {x \ to 1} {\ frac {x ^ {2} -1} {x-1}} = 1 + 1 = 2

Además de los límites en valores finitos, las funciones también pueden tener límites en el infinito. Por ejemplo, considere

f (x) = {2x-1 \ sobre x}

f (100) = 1.9900
f (1000) = 1.9990
f (10000) = 1.99990

A medida que

x

llega a ser extremadamente grande, el valor de

f (x) se

acerca a 2, y el valor de

f (x)

se puede hacer tan cerca de 2 como se podría desear simplemente eligiendo

x

suficientemente grande. En este caso, el límite de

f (x)

cuando

x se

acerca al infinito es 2. En notación matemática,

\ lim _ {x \ to \ infty} {\ frac {2x-1} {x}} = 2.

Límite de una secuencia

Considere la siguiente secuencia: 1.79, 1.799, 1.7999, ... Se puede observar que los números se "acercan" a 1.8, el límite de la secuencia.

Formalmente, supongamos que

un 1, un 2, ...

es una secuencia de números reales. Se puede afirmar que el número real

L

es el límite de esta secuencia, a saber:

\ lim _ {n \ to \ infty} a_ {n} = L

que se lee como

"El límite de a n como n se acerca al infinito es igual a L "

significar

Para cada número real

ε> 0

, existe un número natural

N

tal que para todo

n > N

, tenemos

| a n - L | <ε

.

Intuitivamente, esto significa que, finalmente, todos los elementos de la secuencia se acercan arbitrariamente al límite, ya que el valor absoluto

| a n - L |

es la distancia entre

un n

y

L

. No todas las secuencias tienen un límite; si lo hace, se llama convergente , y si no lo hace, es divergente . Uno puede mostrar que una secuencia convergente tiene solo un límite.

El límite de una secuencia y el límite de una función están estrechamente relacionados. Por un lado, el límite cuando

n

va al infinito de una secuencia

a (n)

es simplemente el límite en el infinito de una función definida en los números naturales

n

. Por otro lado, un límite

L

de una función

f (x)

como

x

va al infinito, si existe, es igual al límite de cualquier secuencia arbitraria

a n

que se acerque a

L

, y donde

a n

nunca es igual a

L

. Una de esas secuencias sería

L + 1 / n

.

Límite como "parte estándar"

En el análisis no estándar (que implica una ampliación hyperreal del sistema de numeración), el límite de una secuencia se puede expresar como la parte estándar del valor de la extensión natural de la secuencia en un índice hipernatural infinito n = H . Así,

(un})

a_ {H}

\ lim _ {n \ to \ infty} a_ {n} = \ operatorname {st} (a_ {H})

.

Aquí la función de la función estándar "st" redondea cada número hiperreal finito al número real más cercano (la diferencia entre ellos es infinitesimal). Esto formaliza la intuición natural de que para los valores "muy grandes" del índice, los términos de la secuencia están "muy cerca" del valor límite de la secuencia. Por el contrario, la parte estándar de un hiperreal representado en la construcción de ultra potencia por una secuencia de Cauchy , es simplemente el límite de esa secuencia:

a = [a_ {n}]

(un})

\ operatorname {st} (a) = \ lim _ {n \ to \ infty} a_ {n}

.

En este sentido, tomar el límite y tomar la parte estándar son procedimientos equivalentes.

Convergencia y punto fijo

Una definición formal de convergencia se puede establecer de la siguiente manera. Supongamos que va de a es una secuencia que converge a , con para todos . Si son constantes positivas y existen con

{{p} _ {n}}

norte

{\ displaystyle 0}

\ infty

pag

{p} _ {n} \ neq p

norte

\ lambda

\alfa

\ lim _ {n \ rightarrow \ infty} {\ frac {\ left | {p} _ {n + 1} -p \ right |} {{\ left | {p} _ {n} -p \ right |} ^ {\ alpha}}} = \ lambda

luego como va de a converge a de orden , con constante de error asintótico

{{p} _ {n}}

norte

{\ displaystyle 0}

\ infty

pag

\alfa

\ lambda

Dada una función con un punto fijo , hay una buena lista de verificación para verificar la convergencia de la secuencia .

F

pag

p_ {n}

1) Primero compruebe que p es de hecho un punto fijo:

f (p) = p

2) Verificar la convergencia lineal. Comience por encontrar . Si....

\ left | f ^ {\ prime} (p) \ right |

$\ left \| f ^ {\ prime} (p) \ right \| \ in (0,1)$	entonces hay convergencia lineal
$\ left \| f ^ {\ prime} (p) \ right \|> 1$	serie diverge
$\ left \| f ^ {\ prime} (p) \ right \| = 0$	entonces hay al menos convergencia lineal y tal vez algo mejor, la expresión debe verificarse para la convergencia cuadrática

3) Si se encuentra que hay algo mejor que lineal, la expresión debe verificarse para la convergencia cuadrática. Comience por encontrar If ....

\ left | f ^ {\ prime \ prime} (p) \ right |

$\ left \| f ^ {\ prime \ prime} (p) \ right \| \ neq 0$	entonces hay una convergencia cuadrática siempre que sea continua $f ^ {\ prime \ prime} (p)$
$\ left \| f ^ {\ prime \ prime} (p) \ right \| = 0$	entonces hay algo incluso mejor que la convergencia cuadrática
$\ left \| f ^ {\ prime \ prime} (p) \ right \|$ no existe	entonces hay una convergencia que es mejor que lineal, pero aún no es cuadrática

Computabilidad del límite

Los límites pueden ser difíciles de calcular. Existen expresiones límite cuyo módulo de convergencia es indecidible. En la teoría de la recursión, el lema Límite demuestra que es posible codificar problemas indecidibles utilizando límites.

Red topológica

Todas las nociones de límite anteriores se pueden unificar y generalizar a espacios topológicos arbitrarios mediante la introducción de redes topológicas y la definición de sus límites.

Una alternativa es el concepto de límite para filtros en espacios topológicos.

Buscar en este blog

Wikiblog Cultulandia [es]

Límite (matemáticas)

Límite (matemáticas)

Definición

Límite de una función

Límite de una secuencia

Límite como "parte estándar"

Convergencia y punto fijo

Computabilidad del límite

Red topológica

Contenidos Relacionados de Matemáticas ››