Péndulo
Definición
Un péndulo es un peso suspendido de un pivote para que pueda oscilar libremente. Cuando un péndulo se desplaza lateralmente desde su posición de equilibrio en reposo, está sujeto a una fuerza de restauración debido a la gravedad que lo acelerará hacia la posición de equilibrio. Cuando se libera, la fuerza de restauración que actúa sobre la masa del péndulo hace que oscile sobre la posición de equilibrio, oscilando hacia adelante y hacia atrás. El tiempo para un ciclo completo, un swing izquierdo y un swing derecho, se llama período. El período depende de la longitud del péndulo y también en un ligero grado de la amplitud, el ancho del balanceo del péndulo.
Desde las primeras investigaciones científicas del péndulo alrededor de 1602 por Galileo Galilei, el movimiento regular de los péndulos se usó para el cronometraje, y fue la tecnología de cronometraje más precisa del mundo hasta la década de 1930. El reloj de péndulo inventado por Christian Huygens en 1658 se convirtió en el cronómetro estándar del mundo, utilizado en hogares y oficinas durante 270 años, y alcanzó una precisión de aproximadamente un segundo por año antes de que fuera reemplazado por el reloj de cuarzo en la década de 1930. Los péndulos también se usan en instrumentos científicos como acelerómetros y sismómetros. Históricamente fueron utilizados como gravímetros para medir la aceleración de la gravedad en estudios geofísicos, e incluso como un estándar de longitud. La palabra "péndulo" es nuevo latín, del latín pendulus , que significa "colgante".
Contenido
- Péndulo de gravedad simple
- Periodo de oscilación
- Péndulo compuesto
- Historia
- 1602: la investigación de Galileo
- 1656: el reloj de péndulo
- 1673: Oscillatorium Horologium de Huygens
- 1721: péndulos compensados por temperatura
- 1851: péndulo de Foucault
- 1930: disminución en el uso
- Uso para medir el tiempo
- Reloj de péndulo
- Compensación de temperatura
- Péndulo de mercurio
- Péndulo de cuadrícula
- Invar y cuarzo fundido
- Presión atmosférica
- Gravedad
- Precisión de los péndulos como cronometradores
- Factor Q
- Escape
- La condición Airy
- Medición de la gravedad
- El péndulo de segundos
- Primeras observaciones
- Péndulo de Kater
- Gravímetros de péndulo posteriores
- Estándar de longitud
- Propuestas tempranas
- El medidor
- Gran Bretaña y Dinamarca
- Otros usos
- Seismómetros
- Ajuste de Schuler
- Péndulos acoplados
- Práctica religiosa
- Educación
- Dispositivo de tortura
Péndulo de gravedad simple
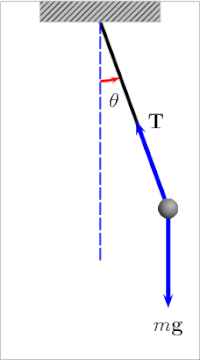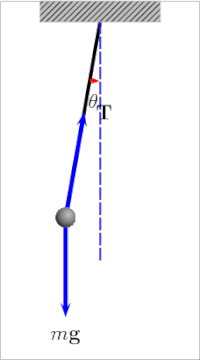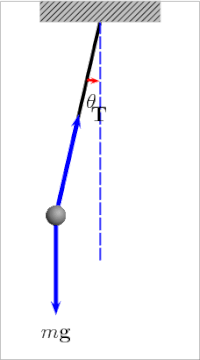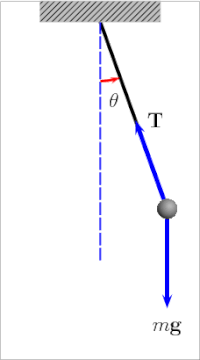
El péndulo de gravedad simple es un modelo matemático idealizado de un péndulo. Este es un peso (o bob) en el extremo de un cordón sin masa suspendido de un pivote, sin fricción. Cuando se le da un empuje inicial, oscilará hacia adelante y hacia atrás a una amplitud constante. Los péndulos reales están sujetos a fricción y arrastre de aire, por lo que la amplitud de sus oscilaciones disminuye.
Periodo de oscilación
El período de oscilación de un péndulo de gravedad simple depende de su longitud, la fuerza de gravedad local y, en menor medida, del ángulo máximo en que el péndulo se aleja de la vertical, θ 0 , llamada amplitud. Es independiente de la masa del bob. Si la amplitud está limitada a oscilaciones pequeñas, el período T de un péndulo simple, el tiempo requerido para un ciclo completo, es:
donde está la longitud del péndulo y es la aceleración local de la gravedad.
Para oscilaciones pequeñas, el período de oscilación es aproximadamente el mismo para diferentes oscilaciones de tamaño: es decir, el período es independiente de la amplitud . Esta propiedad, llamada isocronismo, es la razón por la que los péndulos son tan útiles para la cronometría. Las oscilaciones sucesivas del péndulo, incluso si cambian en amplitud, toman la misma cantidad de tiempo.
Para amplitudes más grandes, el período aumenta gradualmente con la amplitud por lo que es más largo que el dado por la ecuación (1). Por ejemplo, a una amplitud de θ 0 = 23 ° es un 1% más grande que el dado por (1). El período aumenta asintóticamente (hasta el infinito) cuando θ 0 se acerca a 180 °, porque el valor θ 0 = 180 ° es un punto de equilibrio inestable para el péndulo. El período verdadero de un péndulo de gravedad simple ideal se puede escribir en varias formas diferentes (ver Péndulo (matemáticas)), un ejemplo es la serie infinita:
donde está en radianes
La diferencia entre este período verdadero y el período para oscilaciones pequeñas (1) se denomina error circular . En el caso de un reloj de pie típico cuyo péndulo tiene una oscilación de 6 ° y por lo tanto una amplitud de 3 ° (0.05 radianes), la diferencia entre el período verdadero y la aproximación de ángulo pequeño (1) equivale a aproximadamente 15 segundos por día.
Para oscilaciones pequeñas, el péndulo se aproxima a un oscilador armónico, y su movimiento en función del tiempo, t , es aproximadamente un movimiento armónico simple:
donde es un valor constante, depende de las condiciones iniciales.
Para los péndulos reales, el período varía ligeramente con factores tales como la flotabilidad y la resistencia viscosa del aire, la masa de la cuerda o varilla, el tamaño y la forma de la bobina y la forma en que se une a la cuerda, y la flexibilidad y el estiramiento de la cuerda. En aplicaciones de precisión, las correcciones para estos factores pueden necesitar aplicarse a la ecuación. (1) para dar el período con precisión.
Péndulo compuesto
Cualquier cuerpo rígido que se balancee libremente para girar sobre un eje horizontal fijo se denomina péndulo compuesto o péndulo físico . La longitud equivalente apropiada para calcular el período de dicho péndulo es la distancia desde el pivote al centro de oscilación . Este punto se encuentra debajo del centro de masa a una distancia del pivote tradicionalmente llamado radio de oscilación, que depende de la distribución de masa del péndulo. Si la mayor parte de la masa se concentra en un bob relativamente pequeño en comparación con la longitud del péndulo, el centro de oscilación está cerca del centro de masa.
Se puede demostrar que el radio de oscilación o la longitud equivalente de cualquier péndulo físico es
dónde está el momento de inercia del péndulo sobre el punto de pivote, es la masa del péndulo, y es la distancia entre el punto de pivote y el centro de masa. Sustituyendo esta expresión en (1) arriba, el período de un péndulo compuesto está dado por
para oscilaciones suficientemente pequeñas.
Por ejemplo, una varilla rígida uniforme de longitud pivotada alrededor de un extremo tiene un momento de inercia . El centro de masa se encuentra en el centro de la varilla, por lo que la sustitución de estos valores en la ecuación anterior da . Esto muestra que un péndulo de varilla rígida tiene el mismo período que un péndulo simple de 2/3 de su longitud.
Christiaan Huygens demostró en 1673 que el punto de pivote y el centro de oscilación son intercambiables. Esto significa que si un péndulo se pone boca abajo y se balancea desde un pivote ubicado en su centro de oscilación previo, tendrá el mismo período que antes y el nuevo centro de oscilación estará en el punto de pivote anterior. En 1817, Henry Kater utilizó esta idea para producir un tipo de péndulo reversible, ahora conocido como péndulo de Kater, para mejorar las mediciones de la aceleración debida a la gravedad.
Historia
Uno de los primeros usos conocidos de un péndulo fue un dispositivo de sismómetro del siglo 1 del científico chino de la dinastía Han, Zhang Heng. Su función era influir y activar una de una serie de palancas después de ser perturbado por el temblor de un terremoto muy lejano. Liberado por una palanca, una pequeña bola se caería del dispositivo en forma de urna en una de las ocho bocas de sapo de metal debajo, en los ocho puntos de la brújula, lo que significa la dirección en que se localizó el terremoto.
Muchas fuentes afirman que el astrónomo egipcio del siglo X Ibn Yunus usó un péndulo para medir el tiempo, pero este fue un error que se originó en 1684 con el historiador británico Edward Bernard.
Durante el Renacimiento, los grandes péndulos bombeados a mano se utilizaron como fuentes de energía para máquinas recíprocas manuales como sierras, fuelles y bombas. Leonardo da Vinci hizo muchos dibujos del movimiento de los péndulos, aunque sin darse cuenta de su valor para el cronometraje.
1602: la investigación de Galileo
El científico italiano Galileo Galilei fue el primero en estudiar las propiedades de los péndulos, comenzando alrededor de 1602. El primer informe existente de su investigación está en una carta a Guido Ubaldo dal Monte, de Padua, del 29 de noviembre de 1602. Su biógrafo y estudiante, Vincenzo Viviani, afirmó que su interés había sido provocado alrededor de 1582 por el movimiento oscilante de un candelabro en la Catedral de Pisa. Galileo descubrió la propiedad crucial que hace que los péndulos sean útiles como cronometradores, llamado isocronismo; el período del péndulo es aproximadamente independiente de la amplitud o el ancho del columpio. También descubrió que el período es independiente de la masa del bob y es proporcional a la raíz cuadrada de la longitud del péndulo. Primero empleó péndulos libres en aplicaciones de tiempo simple. Su amigo médico, Santorio Santorii, inventó un dispositivo que midió el pulso de un paciente por la longitud de un péndulo; elpulsilogio . En 1641 Galileo concibió y dictó a su hijo Vincenzo un diseño para un reloj de péndulo; Vincenzo comenzó la construcción, pero no la completó cuando murió en 1649. El péndulo fue el primer oscilador armónico utilizado por el hombre.
1656: el reloj de péndulo
En 1656, el científico holandés Christiaan Huygens construyó el primer reloj de péndulo. Esta fue una gran mejora sobre los relojes mecánicos existentes; su mejor precisión se mejoró de alrededor de 15 minutos de desviación por día a alrededor de 15 segundos por día. Los péndulos se extendieron por Europa a medida que los relojes existentes fueron retroadaptados con ellos.
El científico inglés Robert Hooke estudió el péndulo cónico alrededor de 1666, que consiste en un péndulo que se puede balancear libremente en dos dimensiones, con el movimiento giratorio en un círculo o elipse. Usó los movimientos de este dispositivo como modelo para analizar los movimientos orbitales de los planetas. Hooke sugirió a Isaac Newton en 1679 que los componentes del movimiento orbital consistían en un movimiento inercial a lo largo de una dirección tangente más un movimiento atractivo en la dirección radial. Esto jugó un papel en la formulación de Newton de la ley de la gravitación universal. Robert Hooke también fue el responsable de sugerir, ya en 1666, que el péndulo podría usarse para medir la fuerza de la gravedad.
Durante su expedición a Cayena, en la Guayana francesa en 1671, Jean Richer encontró que un reloj de péndulo fue 2 / 2 minutos por día más lenta en Cayena que en París. A partir de esto, dedujo que la fuerza de la gravedad era menor en Cayenne. En 1687, Isaac Newton en Principia Mathematicademostró que esto se debía a que la Tierra no era una esfera verdadera sino ligeramente achatada (aplanada en los polos) por el efecto de la fuerza centrífuga debido a su rotación, lo que causaba que la gravedad aumentara con la latitud. Se comenzaron a tomar péndulos portátiles en viajes a tierras lejanas, como gravímetros de precisión para medir la aceleración de la gravedad en diferentes puntos de la Tierra, lo que finalmente da como resultado modelos precisos de la forma de la Tierra.
1673: Oscillatorium Horologium de Huygens
En 1673, 17 años después de haber inventado el reloj de péndulo, Christiaan Huygens publicó su teoría del péndulo, Horologium Oscillatorium sive de motu pendulorum . Marin Mersenne y René Descartes descubrieron alrededor de 1636 que el péndulo no era bastante isócrono; su período aumentó un poco con su amplitud. Huygens analizó este problema al determinar qué curva debe seguir un objeto para descender por gravedad al mismo punto en el mismo intervalo de tiempo, independientemente del punto de partida; la llamada curva de tautocrona. Mediante un método complicado que fue un uso temprano del cálculo, mostró que esta curva era cicloide, en lugar del arco circular de un péndulo, confirmando que el péndulo no era isócrono y que la observación de isocronismo de Galileo era precisa solo para pequeños cambios. Huygens también resolvió el problema de cómo calcular el período de un péndulo de forma arbitraria (llamado péndulo compuesto ), descubriendo el centro de oscilación y su intercambiabilidad con el punto de pivote.
El movimiento del reloj existente, el escape del borde, hace que los péndulos oscilen en arcos muy anchos de aproximadamente 100 °. Huygens mostró que esto era una fuente de imprecisión, lo que causaba que el período variara con los cambios de amplitud causados por pequeñas variaciones inevitables en la fuerza motriz del reloj. Para hacer su período isócrono, Huygens montó 'chuletas' metálicas en forma de cicloide junto a los pivotes en sus relojes, que restringieron el cordón de la suspensión y obligaron al péndulo a seguir un arco cicloide. Esta solución no resultó tan práctica como simplemente limitar el balanceo del péndulo a pequeños ángulos de algunos grados. La constatación de que solo pequeñas oscilaciones eran isócronas motivó el desarrollo del escape del ancla alrededor de 1670, que redujo el oscilación del péndulo en los relojes a 4 ° -6 °.
1721: péndulos compensados por temperatura
Durante los siglos XVIII y XIX, el reloj de péndulo como el cronometrador más preciso motivó mucha investigación práctica para mejorar los péndulos. Se encontró que una fuente principal de error fue que la varilla del péndulo se expandió y se contrajo con los cambios en la temperatura ambiente, cambiando el período de oscilación. Esto se resolvió con la invención de péndulos con compensación de temperatura, el péndulo de mercurio en 1721 y el péndulo de la parrilla en 1726, reduciendo los errores en los relojes de péndulo de precisión a unos pocos segundos por semana.
La precisión de las mediciones de gravedad hechas con péndulos estaba limitada por la dificultad de encontrar la ubicación de su centro de oscilación. Huygens descubrió en 1673 que un péndulo tiene el mismo período cuando se cuelga de su centro de oscilación que cuando se cuelga de su pivote, y la distancia entre los dos puntos era igual a la longitud de un péndulo de gravedad simple del mismo período. En 1818, el capitán británico Henry Kater inventó el péndulo de Kater reversible que utilizaba este principio, posibilitando mediciones muy precisas de la gravedad. Para el próximo siglo, el péndulo reversible era el método estándar para medir la aceleración gravitacional absoluta.
1851: péndulo de Foucault
En 1851, Jean Bernard Léon Foucault demostró que el plano de oscilación de un péndulo, como un giroscopio, tiende a mantenerse constante independientemente del movimiento del pivote, y que esto podría usarse para demostrar la rotación de la Tierra. Colgó un péndulo libre para columpiarse en dos dimensiones (más tarde llamado el péndulo de Foucault) desde la cúpula del Panteón en París. La longitud del cable era de 67 m (220 pies). Una vez que el péndulo se puso en movimiento, se observó que el plano de oscilación precede o gira 360 ° en el sentido de las agujas del reloj en aproximadamente 32 horas. Esta fue la primera demostración de la rotación de la Tierra que no dependió de las observaciones celestiales, y estalló una "manía pendular", ya que los péndulos de Foucault se exhibían en muchas ciudades y atraían a grandes multitudes.
1930: disminución en el uso
Alrededor de 1900 se comenzaron a utilizar materiales de baja expansión térmica para varillas pendulares en relojes de alta precisión y otros instrumentos, primero invar, una aleación de acero al níquel y, posteriormente, cuarzo fundido, lo que hizo que la compensación de temperatura fuera trivial. Los péndulos de precisión se alojaron en tanques de baja presión, lo que mantuvo la presión de aire constante para evitar cambios en el período debido a los cambios en la flotabilidad del péndulo debido a la presión atmosférica cambiante. Los mejores relojes de péndulo lograron una precisión de alrededor de un segundo por año.
La precisión del cronómetro del péndulo fue superada por el oscilador de cristal de cuarzo, inventado en 1921, y los relojes de cuarzo, inventados en 1927, reemplazaron a los relojes de péndulo como los mejores cronometradores del mundo. Los relojes de péndulo se usaron como patrones de tiempo hasta la Segunda Guerra Mundial, aunque los franceses Time Service continuó utilizándolos en su conjunto estándar de tiempo oficial hasta 1954. Los gravímetros pendulares fueron reemplazados por los "gravímetros de caída libre" en la década de 1950, pero los instrumentos de péndulo continuaron siendo utilizados en la década de 1970.
Uso para medir el tiempo
Durante 300 años, desde su descubrimiento alrededor de 1582 hasta el desarrollo del reloj de cuarzo en la década de 1930, el péndulo era el estándar mundial para el cronometraje preciso. Además de los péndulos de reloj, los péndulos de segundos libres se usaron ampliamente como temporizadores de precisión en experimentos científicos en los siglos XVII y XVIII. Los péndulos requieren una gran estabilidad mecánica: un cambio de longitud de solo 0,02%, 0,2 mm en un péndulo de reloj de pie, causará un error de un minuto por semana.
Reloj de péndulo
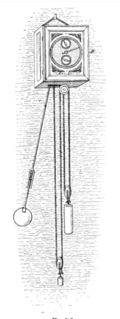
Los péndulos en los relojes (ver el ejemplo a la derecha) generalmente están hechos de un peso o bob (b) suspendido por una varilla de madera o metal (a). Para reducir la resistencia del aire (que representa la mayor parte de la pérdida de energía en relojes de precisión), el bob es tradicionalmente un disco liso con una sección transversal en forma de lente, aunque en relojes antiguos a menudo tenía esculturas o decoraciones específicas para el tipo de reloj. En relojes de calidad, el bob es tan pesado como la suspensión puede soportar y el movimiento puede conducir, ya que mejora la regulación del reloj (ver Accuracybelow). Un peso común para segundos oscilaciones del péndulo es de 15 libras (6,8 kg). En lugar de colgarse de un pivote, los péndulos de reloj suelen estar soportados por un resorte recto corto (d)de cinta de metal flexible. Esto evita la fricción y el "juego" causado por un pivote, y la ligera fuerza de flexión del muelle simplemente se suma a la fuerza de restauración del péndulo. Unos pocos relojes de precisión tienen pivotes de cuchillas de 'cuchillos' que descansan sobre placas de ágata. Los impulsos para mantener el péndulo balanceándose son proporcionados por un brazo que cuelga detrás del péndulo llamado muleta , (e) , que termina en una horquilla , (f) cuyos dientes abrazan la varilla del péndulo. La muleta es empujada hacia adelante y hacia atrás por el escape del reloj, (g, h) .
Cada vez que el péndulo oscila en su posición central, libera un diente de la rueda de escape (g) . La fuerza del muelle principal del reloj o un peso de conducción colgando de una polea, transmitida a través del tren de engranajes del reloj, hace que la rueda gire y un diente presiona contra una de las paletas (h) , dando al péndulo un breve impulso. Las ruedas del reloj, adaptadas a la rueda de escape, avanzan una cantidad fija con cada oscilación del péndulo, avanzando las agujas del reloj a un ritmo constante.
El péndulo siempre tiene un medio para ajustar el período, por lo general mediante una tuerca de ajuste (c) debajo del bob que lo mueve hacia arriba o hacia abajo en la varilla. Mover la sacudida hacia arriba disminuye la longitud del péndulo, haciendo que el péndulo oscile más rápido y el reloj gane tiempo. Algunos relojes de precisión tienen un pequeño peso de ajuste auxiliar en un eje roscado en el bob, para permitir un ajuste más fino. Algunos relojes de torre y relojes de precisión usan una bandeja unida cerca del punto medio de la varilla del péndulo, a la cual se pueden agregar o quitar pequeños pesos. Esto efectivamente cambia el centro de oscilación y permite ajustar la velocidad sin detener el reloj.
El péndulo debe estar suspendido de un soporte rígido. Durante la operación, cualquier elasticidad permitirá pequeños movimientos imperceptibles de balanceo del soporte, lo que altera el período del reloj, lo que genera un error. Los relojes de péndulo deben sujetarse firmemente a una pared resistente.
La longitud de péndulo más común en los relojes de calidad, que siempre se usa en los relojes de pie, es el péndulo de segundos, de aproximadamente 1 metro (39 pulgadas) de largo. En los relojes Mantel, se usan péndulos de medio segundo, de 25 cm (9,8 in) de largo o más cortos. Solo unos pocos relojes de torre grandes usan péndulos más largos, el péndulo de 1,5 segundos, 2,25 m (7,4 pies) de largo, u ocasionalmente el péndulo de dos segundos, 4 m (13 pies) que se usa en Big Ben.
Compensación de temperatura
La mayor fuente de error en los primeros péndulos fue pequeños cambios en la longitud debido a la expansión térmica y contracción de la varilla del péndulo con cambios en la temperatura ambiente. Esto se descubrió cuando las personas notaron que los relojes de péndulo corrían más despacio en verano, hasta en un minuto por semana (uno de los primeros fue Godefroy Wendelin, según lo informado por Huygens en 1658). La expansión térmica de las varillas pendulares fue estudiada por primera vez por Jean Picard en 1669. Un péndulo con una varilla de acero se expandirá alrededor de 11.3 partes por millón (ppm) con cada grado Celsius de aumento, causando que pierda 0.27 segundos por día por cada grado Celsius aumento en la temperatura, o 9 segundos por día para un cambio de 33 ° C (59 ° F). Las varillas de madera se expanden menos, perdiendo solo alrededor de 6 segundos por día para un cambio de 33 ° C (59 ° F), por lo que los relojes de calidad a menudo tenían varillas de péndulo de madera.
Péndulo de mercurio
El primer dispositivo para compensar este error fue el péndulo de mercurio, inventado por George Graham en 1721. El metal líquido de mercurio se expande en volumen con la temperatura. En un péndulo de mercurio, el peso del péndulo (bob) es un contenedor de mercurio. Con un aumento de temperatura, la varilla del péndulo se alarga, pero el mercurio también se expande y su nivel de superficie aumenta ligeramente en el recipiente, moviendo su centro de masa más cerca del pivote del péndulo. Al usar la altura correcta de mercurio en el contenedor, estos dos efectos se cancelarán, dejando el centro de masa del péndulo y su período sin cambios con la temperatura. Su principal desventaja era que cuando cambiaba la temperatura, la varilla llegaría a la nueva temperatura rápidamente, pero la masa de mercurio podría tardar uno o dos días en alcanzar la nueva temperatura, lo que provocaría que la tasa se desviara durante ese tiempo. Para mejorar la acomodación térmica, a menudo se usaban varios recipientes delgados, hechos de metal. Los péndulos de mercurio eran el estándar utilizado en los relojes de precisión del regulador en el siglo XX.
Péndulo de cuadrícula
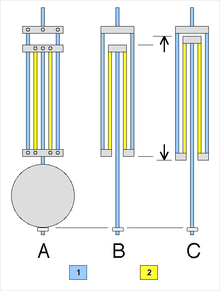
El péndulo compensado más utilizado fue el péndulo de la parrilla, inventado en 1726 por John Harrison. Este consiste en varillas alternas de dos metales diferentes, una con menor expansión térmica (CTE), acero y una con mayor expansión térmica, zinc o latón. Las barras están conectadas por un marco, como se muestra en el dibujo de la derecha, de modo que un aumento en la longitud de las varillas de zinc empuja la bobina hacia arriba, acortando el péndulo. Con un aumento de temperatura, las varillas de acero de baja expansión hacen que el péndulo sea más largo, mientras que las varillas de zinc de alta expansión lo hacen más corto. Al hacer las barras de las longitudes correctas, la mayor expansión del zinc cancela la expansión de las varillas de acero que tienen una longitud combinada mayor, y el péndulo se mantiene la misma longitud con la temperatura.
Los péndulos de acero de zinc están hechos con 5 varillas, pero la expansión térmica del latón está más cerca del acero, por lo que las rejillas de latón por lo general requieren 9 varillas. Los péndulos de Gridiron se ajustan a los cambios de temperatura más rápido que los péndulos de mercurio, pero los científicos descubrieron que la fricción de las varillas deslizándose en sus agujeros en el marco hacía que los péndulos de la parrilla se ajustaran en una serie de pequeños saltos. En los relojes de alta precisión, esto hizo que la frecuencia del reloj cambiara repentinamente con cada salto. Más tarde se descubrió que el zinc está sujeto a fluencia. Por estas razones, los péndulos de mercurio se usaron en los relojes de mayor precisión, pero las rejillas se usaron en los relojes con regulador de calidad.
Los péndulos de Gridiron llegaron a estar tan asociados con la buena calidad que, hasta el día de hoy, muchos péndulos de reloj ordinarios tienen rejillas decorativas "falsas" que en realidad no tienen ninguna función de compensación de temperatura.
Invar y cuarzo fundido
Alrededor de 1900, se desarrollaron materiales de baja expansión térmica que podrían utilizarse como barras de péndulo con el fin de hacer innecesaria una complicada compensación de temperatura. Estos solo se usaron en algunos de los relojes de mayor precisión antes de que el péndulo se volviera obsoleto como estándar de tiempo. En 1896 Charles Édouard Guillaume inventó la aleación de acero al níquel Invar. Tiene un CET de alrededor de 0.5 μin / (in • ° F), lo que da como resultado errores de temperatura del péndulo superiores a 71 ° F de solo 1.3 segundos por día, y este error residual podría compensarse a cero con unos pocos centímetros de aluminio debajo del péndulo bob (esto se puede ver en la imagen del reloj Riefler arriba). Los péndulos Invar se usaron por primera vez en 1898 en el reloj regulador Riefler, que alcanzó una precisión de 15 milisegundos por día. Los resortes de suspensión de Elinvar se usaron para eliminar la variación de temperatura de la primavera ' s fuerza de restauración en el péndulo. Posteriormente se utilizó cuarzo fundido que tenía CTE incluso más bajo. Estos materiales son la opción para péndulos modernos de alta precisión.
Presión atmosférica
El efecto del aire circundante sobre un péndulo en movimiento es complejo y requiere una mecánica de fluidos para calcular con precisión, pero para la mayoría de los propósitos, su influencia en el período puede explicarse por tres efectos:
- Según el principio de Arquímedes, el peso efectivo del bob se reduce por la flotabilidad del aire que desplaza, mientras que la masa (inercia) permanece igual, reduciendo la aceleración del péndulo durante su oscilación y aumentando el período. Esto depende de la presión del aire y la densidad del péndulo, pero no su forma.
- El péndulo transporta una cantidad de aire cuando se balancea, y la masa de este aire aumenta la inercia del péndulo, reduciendo de nuevo la aceleración y aumentando el período. Esto depende de su densidad y forma.
- La resistencia del aire viscoso reduce la velocidad del péndulo. Esto tiene un efecto insignificante en el período, pero disipa la energía, reduciendo la amplitud. Esto reduce el factor Q del péndulo, lo que requiere una fuerza impulsora más fuerte del mecanismo del reloj para mantenerlo en movimiento, lo que causa una mayor perturbación del período.
Los aumentos en la presión barométrica aumentan ligeramente el período de un péndulo debido a los dos primeros efectos, en aproximadamente 0,11 segundos por día por kilopascal (0,37 segundos por día por pulgada de mercurio o 0,015 segundos por día por torr). Los investigadores que usan péndulos para medir la aceleración de la gravedad tuvieron que corregir el período de la presión del aire a la altitud de medición, calculando el período equivalente de un péndulo oscilando en el vacío. Un reloj de péndulo fue operado por primera vez en un tanque de presión constante por Friedrich Tiede en 1865 en el Observatorio de Berlín, y en 1900 los relojes de mayor precisión se montaron en tanques que se mantuvieron a presión constante para eliminar los cambios en la presión atmosférica. Alternativamente, en algunos, un pequeño mecanismo barómetro aneroide unido al péndulo compensó este efecto.
Gravedad
Los péndulos se ven afectados por los cambios en la aceleración de la gravedad, que varía hasta en un 0,5% en diferentes lugares de la Tierra, por lo que los relojes de péndulo de precisión tienen que ser recalibrados después de un movimiento. Incluso mover un reloj de péndulo a la parte superior de un edificio alto puede hacer que pierda tiempo medible debido a la reducción de la gravedad.
Precisión de los péndulos como cronometradores
Los elementos de cronometraje en todos los relojes, que incluyen péndulos, ruedas de equilibrio, los cristales de cuarzo utilizados en los relojes de cuarzo, e incluso los átomos que vibran en los relojes atómicos, en física se llaman osciladores armónicos. La razón por la que los osciladores armónicos se usan en los relojes es que vibran u oscilan a una frecuencia o período resonante específico y resisten a oscilar a otras velocidades. Sin embargo, la frecuencia de resonancia no es infinitamente 'aguda'. Alrededor de la frecuencia resonante hay una banda natural estrecha de frecuencias (o periodos), llamada ancho de resonancia o ancho de banda, donde el oscilador armónico oscilará. En un reloj, la frecuencia real del péndulo puede variar aleatoriamente dentro de este ancho de resonancia en respuesta a las perturbaciones, pero en las frecuencias fuera de esta banda, el reloj no funcionará en absoluto.
Factor Q
La medida de la resistencia de un oscilador armónico a las perturbaciones de su período de oscilación es un parámetro adimensional llamado factor Q igual a la frecuencia resonante dividido por el ancho de resonancia. Cuanto mayor es Q , menor es el ancho de resonancia, y más constante es la frecuencia o el período del oscilador para una perturbación determinada. El recíproco de Q es aproximadamente proporcional a la precisión límite que puede alcanzar un oscilador armónico como estándar de tiempo.
La Q está relacionada con el tiempo que tardan las oscilaciones de un oscilador en desaparecer. La Q de un péndulo se puede medir contando el número de oscilaciones que toma para que la amplitud del balanceo del péndulo decaiga a 1 / e = 36.8% de su oscilación inicial, y multiplicando por 2 π .
En un reloj, el péndulo debe recibir impulsos del movimiento del reloj para mantenerlo balanceándose, para reemplazar la energía que el péndulo pierde a la fricción. Estos impulsos, aplicados por un mecanismo llamado escape, son la principal fuente de perturbación del movimiento del péndulo. La Q es igual a 2 π veces la energía almacenada en el péndulo, dividida por la energía perdida por la fricción durante cada período de oscilación, que es la misma que la energía agregada por el escape en cada período. Se puede observar que cuanto menor es la fracción de la energía del péndulo que se pierde por fricción, menor es la energía que se necesita agregar, cuanto menos perturba el escape, más independiente es el péndulo del mecanismo del reloj y el más constante es su período. La Q de un péndulo está dado por:
donde M es la masa del bob, ω = 2 π / T es la frecuencia de oscilación radiante del péndulo, y Γ es la fuerza de amortiguación friccional en el péndulo por unidad de velocidad.
ω se fija por el período del péndulo, y M está limitado por la capacidad de carga y la rigidez de la suspensión. Por lo tanto, la Q de los péndulos de reloj aumenta al minimizar las pérdidas por fricción ( Γ ). Los péndulos de precisión están suspendidos en pivotes de baja fricción que consisten en bordes de "cuchilla" de forma triangular que descansan sobre placas de ágata. Alrededor del 99% de la pérdida de energía en un péndulo que se mueve libremente se debe a la fricción del aire, por lo que montar un péndulo en un tanque de vacío puede aumentar la Q , y por lo tanto la precisión, en un factor de 100.
La Q de péndulos oscila entre varios miles en un reloj ordinario a varios cientos de miles para péndulos reguladores de precisión que se balancean en el vacío. Un reloj de péndulo casero de calidad podría tener una Q de 10,000 y una precisión de 10 segundos por mes. El reloj de péndulo más preciso producido comercialmente fue el reloj de péndulo libre Shortt-Synchronome, inventado en 1921. Su péndulo principal Invar oscilando en un tanque de vacío tenía una Q de 110,000 y un índice de error de alrededor de un segundo por año.
Su Q de 10-10 es una de las razones por las que los péndulos son cronómetros más precisos que las ruedas de equilibrio en los relojes, con Q alrededor de 100-300, pero menos precisa que los cristales de cuarzo en los relojes de cuarzo, con Q de 10-10.
Escape
Los péndulos (a diferencia, por ejemplo, de los cristales de cuarzo) tienen una Q lo suficientemente baja como para que la perturbación causada por los impulsos para mantenerlos en movimiento sea generalmente el factor limitante en la precisión de su cronometraje. Por lo tanto, el diseño del escape, el mecanismo que proporciona estos impulsos, tiene un gran efecto en la precisión de un péndulo de reloj. Si los impulsos dados al péndulo por el escape cada oscilación pudieran ser exactamente idénticos, la respuesta del péndulo sería idéntica, y su período sería constante. Sin embargo, esto no es alcanzable; Las fluctuaciones aleatorias inevitables en la fuerza debidas a la fricción de las paletas del reloj, las variaciones de lubricación y los cambios en el par proporcionado por la fuente de alimentación del reloj a medida que desciende, significan que la fuerza del impulso aplicado por el escape varía.
Si estas variaciones en la fuerza del escape causan cambios en el ancho de oscilación del péndulo (amplitud), esto provocará los correspondientes pequeños cambios en el período, ya que (como se explica en la parte superior) un péndulo con un balanceo finito no es bastante isócrono. Por lo tanto, el objetivo del diseño de escape tradicional es aplicar la fuerza con el perfil adecuado y en el punto correcto en el ciclo del péndulo, de modo que las variaciones de fuerza no tengan ningún efecto sobre la amplitud del péndulo. Esto se llama un escape isócrono .
La condición Airy
En 1826, el astrónomo británico George Airy demostró lo que los relojeros habían sabido durante siglos; que el efecto perturbador de una fuerza motriz sobre el período de un péndulo es menor si se da como un impulso corto cuando el péndulo pasa a través de su posición de equilibrio inferior. Específicamente, demostró que si un péndulo es impulsado por un impulso que es simétrico con respecto a su posición de equilibrio inferior, el período del péndulo no se verá afectado por los cambios en la fuerza de accionamiento. Los escapes más precisos, como el deadbeat, satisfacen aproximadamente esta condición.
Medición de la gravedad
La presencia de la aceleración de la gravedad g en la ecuación de periodicidad (1) para un péndulo significa que la aceleración gravitacional local de la Tierra se puede calcular a partir del período de un péndulo. Por lo tanto, un péndulo puede usarse como un gravímetro para medir la gravedad local, que varía en más del 0.5% a través de la superficie de la Tierra. El péndulo en un reloj se ve perturbado por los empujes que recibe del movimiento del reloj, por lo que se usaron péndulos que se desplazan libremente, y fueron los instrumentos estándar de la gravimetría hasta la década de 1930.
La diferencia entre los péndulos del reloj y los péndulos del gravímetro es que, para medir la gravedad, se debe medir tanto la longitud del péndulo como su período. El período de péndulos libres se podía encontrar con gran precisión al comparar su swing con un reloj de precisión que se había ajustado para mantener el tiempo correcto mediante el paso de las estrellas sobre su cabeza. En las primeras mediciones, un peso sobre un cordón se suspendió frente al péndulo del reloj, y su longitud se ajustó hasta que los dos péndulos se balancearon en sincronismo exacto. Luego se midió la longitud del cordón. A partir de la longitud y el período, g podría calcularse a partir de la ecuación (1).
El péndulo de segundos
El péndulo de segundos, un péndulo con un período de dos segundos para que cada oscilación tome un segundo, se usaba ampliamente para medir la gravedad, porque su período podía medirse fácilmente comparándolo con relojes de precisión del regulador, que tenían péndulos en segundos. A fines del siglo XVII, la longitud del péndulo de segundos se convirtió en la medida estándar de la fuerza de la aceleración gravitacional en un lugar. En 1700, su longitud se había medido con precisión submilimétrica en varias ciudades de Europa. Durante un péndulo de segundos, g es proporcional a su longitud:
Primeras observaciones
- 1620 : El científico británico Francis Bacon fue uno de los primeros en proponer el uso de un péndulo para medir la gravedad, lo que sugiere subir una montaña para ver si la gravedad varía con la altitud.
- 1644 : incluso antes del reloj de péndulo, el sacerdote francés Marin Mersenne determinó por primera vez que la longitud del péndulo de segundos era de 39,1 pulgadas (990 mm), al comparar el balanceo de un péndulo con el tiempo que tardó un peso en caer una distancia medida.
- 1669 : Jean Picard determina la longitud del péndulo de segundos en París, usando una bola de cobre de 1 pulgada (25 mm) suspendida por una fibra de aloe, obteniendo 39.09 pulgadas (993 mm).
- 1672 : La primera observación que la gravedad varía en diferentes puntos de la Tierra fue hecha en 1672 por Jean Richer, que tomó un reloj de péndulo de Cayena, en la Guayana francesa y se encontró que perdió 2 / 2 minutos por día; su segundo péndulo tuvo que ser acortado por 1 / 4 lignes (2,6 mm) más corto que en París, para mantener el tiempo correcto. En 1687 Isaac Newton en Principia Mathematicamostró que esto se debía a que la Tierra tenía una forma ligeramente oblata (aplanada en los polos) causada por la fuerza centrífuga de su rotación. En latitudes más altas, la superficie estaba más cerca del centro de la Tierra, por lo que la gravedad aumentaba con la latitud. A partir de este momento, los péndulos comenzaron a ser llevados a tierras lejanas para medir la gravedad, y se compilaron tablas de la longitud del péndulo de segundos en diferentes lugares de la Tierra. En 1743, Alexis Claude Clairaut creó el primer modelo hidrostático de la Tierra, el teorema de Clairaut, que permitía calcular la elipticidad de la Tierra a partir de las mediciones de la gravedad. Se siguieron modelos progresivamente más precisos de la forma de la Tierra.
- 1687 : Newton experimentó con péndulos (descritos en Principia ) y descubrió que los péndulos de igual longitud con bobs hechos de diferentes materiales tenían el mismo período, lo que demuestra que la fuerza gravitacional sobre diferentes sustancias era exactamente proporcional a su masa (inercia).
- 1737 : el matemático francés Pierre Bouguer realizó una sofisticada serie de observaciones de péndulo en la cordillera de los Andes, Perú. Utilizó un péndulo de cobre en forma de cono doble puntiagudo suspendido por un hilo; el bob podría invertirse para eliminar los efectos de la densidad no uniforme. Calculó la longitud del centro de oscilación del hilo y el bob combinados, en lugar de usar el centro del bob. Corrigió la expansión térmica de la varilla de medición y la presión barométrica, dando sus resultados para un péndulo balanceándose en el vacío. Bouguer balanceó el mismo péndulo en tres elevaciones diferentes, desde el nivel del mar hasta la cima del alto altiplano peruano. La gravedad debería caer con el cuadrado inverso de la distancia desde el centro de la Tierra. Bouguer descubrió que caía más lentamente y atribuía correctamente la gravedad "extra" al campo gravitacional de la enorme meseta peruana. A partir de la densidad de las muestras de roca, calculó una estimación del efecto del altiplano en el péndulo, y al comparar esto con la gravedad de la Tierra, pudo hacer la primera estimación aproximada de la densidad de la Tierra.
- 1747 : Daniel Bernoulli mostró cómo corregir para el alargamiento del período debido a un ángulo finito de giro θ 0 mediante el uso de la primera corrección para θ 0 /16, dando el periodo de un péndulo con una extremadamente pequeña oscilación.
- 1792 : Para definir un estándar de péndulo de longitud para usar con el nuevo sistema métrico, en 1792 Jean-Charles de Borda y Jean-Dominique Cassini hicieron una medición precisa del péndulo de segundos en París. Utilizaron un 1 / 2 balón platino pulgadas (14 mm) suspendida por un alambre de hierro de 12 pies (3,7 m). Su principal innovación fue una técnica llamada " método de coincidencias " que permitió comparar el período de péndulos con gran precisión. (Bouguer también había usado este método). El intervalo de tiempo Δ T entre los instantes recurrentes cuando los dos péndulos oscilaron en sincronismo fue temporizado. A partir de esto, la diferencia entre los períodos de los péndulos, T 1 y T 2, podría ser calculado:
- 1821 : Francesco Carlini hizo observaciones pendulares en la cima del Monte Cenis, Italia, desde donde, usando métodos similares a los de Bouguer, calculó la densidad de la Tierra. Comparó sus mediciones con una estimación de la gravedad en su ubicación, suponiendo que la montaña no estaba allí, calculada a partir de mediciones de péndulos cercanas anteriores a nivel del mar. Sus medidas mostraron un "exceso" de gravedad, que asignó al efecto de la montaña. Modelando la montaña como un segmento de una esfera de 11 millas (18 km) de diámetro y 1 milla (1,6 km) de altura, a partir de muestras de rocas, calculó su campo gravitatorio y estimó la densidad de la Tierra a 4.39 veces la del agua. Recalculaciones posteriores de otros dieron valores de 4.77 y 4.95, ilustrando las incertidumbres en estos métodos geográficos.
Péndulo de Kater
La precisión de las mediciones de la gravedad principios anteriores estaba limitado por la dificultad de medir la longitud del péndulo, L . L era la longitud de un péndulo de gravedad simple idealizado (descrito en la parte superior), que tiene toda su masa concentrada en un punto al final de la cuerda. En 1673 Huygens había demostrado que el período de un péndulo de barra rígido (llamado péndulo compuesto ) era igual al período de un péndulo simple con una longitud igual a la distancia entre el punto de pivote y un punto llamado el centro de oscilación, ubicado debajo el centro de gravedad, que depende de la distribución de la masa a lo largo del péndulo. Pero no había una forma precisa de determinar el centro de oscilación en un péndulo real.
Para evitar este problema, los primeros investigadores se aproximaron lo más posible a un péndulo simple ideal utilizando una esfera metálica suspendida por un cable o cuerda liviana. Si el cable era lo suficientemente ligero, el centro de oscilación estaba cerca del centro de gravedad de la bola, en su centro geométrico. Este tipo de péndulo de "bola y alambre" no era muy preciso, porque no se balanceaba como un cuerpo rígido, y la elasticidad del alambre hacía que su longitud cambiara ligeramente a medida que el péndulo oscilaba.
Sin embargo, Huygens también había demostrado que en cualquier péndulo, el punto de pivote y el centro de oscilación eran intercambiables. Es decir, si un péndulo fuera volteado y colgado de su centro de oscilación, tendría el mismo período que lo hacía en la posición anterior, y el antiguo punto de pivote sería el nuevo centro de oscilación.
El físico británico y capitán del ejército Henry Kater en 1817 se dio cuenta de que el principio de Huygens podría usarse para hallar la longitud de un péndulo simple con el mismo período que un péndulo real. Si se construyó un péndulo con un segundo punto de pivote ajustable cerca de la parte inferior para poder colgar boca abajo, y el segundo pivote se ajustó hasta que los períodos de ambos pivotes fueran iguales, el segundo pivote estaría en el centro de oscilación , y la distancia entre los dos pivotes sería la longitud L de un péndulo simple con el mismo período.
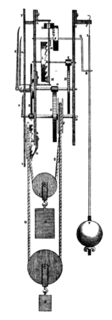
Kater construyó un péndulo reversible (que se muestra a la derecha) que consiste en una barra de bronce con dos pivotes opuestos hechos de cortas cuchillas triangulares "de cuchillo" (a) cerca de cada extremo. Se podía oscilar desde cualquier pivote, con las cuchillas apoyadas en placas de ágata. En lugar de hacer un pivote ajustable, ató los pivotes a un metro de distancia y en su lugar ajustó los períodos con un peso móvil en la varilla del péndulo (b, c) . En funcionamiento, el péndulo se cuelga delante de un reloj de precisión, y el período se mide, se gira y el período se vuelve a programar. El peso se ajusta con el tornillo de ajuste hasta que los períodos sean iguales. Luego, poner este período y la distancia entre los pivotes en la ecuación (1) da la aceleración gravitacional g con mucha precisión.
Kater cronometró el balanceo de su péndulo usando el " método de coincidencias " y midió la distancia entre los dos pivotes con un micrómetro. Después de aplicar correcciones para la amplitud finita del balanceo, la flotabilidad de la sacudida, la presión barométrica, la altitud y la temperatura, obtuvo un valor de 39.13929 pulgadas para el péndulo de segundos en Londres, en el vacío, a nivel del mar, a 62 ° F . La mayor variación con respecto a la media de sus 12 observaciones fue de 0.00028 in, lo que representa una precisión de la medición de la gravedad de 7 × 10 (7 mGal o 70 μm / s). La medida de Kater se usó como el estándar oficial de longitud de Gran Bretaña (ver abajo) de 1824 a 1855.
Los péndulos reversibles (conocidos técnicamente como péndulos "convertibles") que emplean el principio de Kater se usaron para las mediciones de la gravedad absoluta en la década de 1930.
Gravímetros de péndulo posteriores
La mayor precisión posible gracias al péndulo de Kater ayudó a que la gravimetría fuera una parte estándar de la geodesia. Dado que la ubicación exacta (latitud y longitud) de la 'estación' donde se realizó la medición de la gravedad era necesario, mediciones de la gravedad se convirtieron en parte de la topografía, y péndulos se tomaron en los grandes estudios geodésicos del siglo 18, en particular la Encuesta Gran trigonométricas de India.
- Péndulos invariables: Kater introdujo la idea de las medidas relativas de la gravedad, para complementar el valor absolutomediciones hechas por un péndulo de Kater. Comparar la gravedad en dos puntos diferentes fue un proceso más fácil que medirlo absolutamente con el método de Kater. Todo lo que se necesitaba era cronometrar el período de un péndulo ordinario (pivote único) en el primer punto, luego transportar el péndulo al otro punto y medir el tiempo allí. Dado que la longitud del péndulo era constante, a partir de (1) la relación de las aceleraciones gravitacionales era igual a la inversa de la relación de los períodos cuadrados, y no hay mediciones de longitud de precisión eran necesarias. Así que una vez que la gravedad se había medido absolutamente en algún estación central, por el Kater u otro método preciso, la gravedad en otros puntos se pudo encontrar balanceando péndulos en la estación central y luego llevarlos a otro lugar y el momento de su apogeo allí.
- Experimentos del pozo de carbón de Airy: Comenzando en 1826, usando métodos similares a Bouguer, el astrónomo británico George Airy intentó determinar la densidad de la Tierra mediante mediciones de gravedad pendular en la parte superior e inferior de una mina de carbón. La fuerza gravitacional debajo de la superficie de la Tierra disminuye en vez de aumentar con la profundidad, porque según la ley de Gauss, la masa de la capa esférica de la corteza sobre el punto subsuperficial no contribuye a la gravedad. El experimento de 1826 fue abortado por la inundación de la mina, pero en 1854 condujo un experimento mejorado en la mina de carbón de Harton, utilizando segundos péndulos balanceándose en placas de ágata, sincronizados por cronómetros de precisión sincronizados por un circuito eléctrico. Descubrió que el péndulo inferior era más lento en 2,24 segundos por día. Esto significaba que la aceleración gravitacional en el fondo de la mina, 1250 pies debajo de la superficie, fue 1 / 14,000 menos de lo que debería haber sido de la ley del cuadrado inverso; esa es la atracción de la capa esférica que era 1/14,000 de la atracción de la Tierra. A partir de muestras de rocas superficiales, estimó la masa del caparazón esférico de la corteza y, a partir de esto, estimó que la densidad de la Tierra era 6.565 veces mayor que la del agua. Von Sterneck intentó repetir el experimento en 1882 pero encontró resultados inconsistentes.
- Péndulo de Repsol-Bessel:Llevaba mucho tiempo y era propenso a errores mover repetidamente el péndulo de Kater y ajustar los pesos hasta que los períodos fueran iguales. Friedrich Bessel demostró en 1835 que esto era innecesario. Siempre que los períodos estuvieran próximos, la gravedad podría calcularse a partir de los dos períodos y el centro de gravedad del péndulo. Por lo tanto, el péndulo reversible no necesitaba ser ajustable, solo podía ser una barra con dos pivotes. Bessel también demostró que si el péndulo se hacía simétricamente en forma alrededor de su centro, pero se pesaba internamente en un extremo, los errores debidos a la resistencia del aire se cancelarían. Además, otro error debido al diámetro finito de los bordes de la cuchilla podría cancelarse si se intercambiaran entre mediciones. Bessel no construyó tal péndulo, pero en 1864 Adolf Repsold, bajo contrato por la Comisión Geodésica Suiza hizo un péndulo en esta línea. El péndulo de Repsold tenía aproximadamente 56 cm de largo y tenía un período de aproximadamente/ 4 segundos. Fue utilizado ampliamente por las agencias geodésicas europeas, y con el péndulo de Kater en la Encuesta de la India. Péndulos similares de este tipo fueron diseñados por Charles Pierce y C. Defforges.
- Gravímetros de Von Sterneck y Mendenhall: en 1887, el científico austrohúngaro Robert von Sterneck desarrolló un pequeño péndulo gravimétrico montado en un tanque de vacío con temperatura controlada para eliminar los efectos de la temperatura y la presión del aire. Usó un "péndulo de medio segundo", con un período cercano a un segundo, de unos 25 cm de largo. El péndulo no era reversible, por lo que el instrumento se usó para medir la gravedad relativa, pero su pequeño tamaño los hizo pequeños y portátiles. El período del péndulo fue recogido al reflejar la imagen de una chispa eléctrica creada por un cronómetro de precisión de un espejo montado en la parte superior de la varilla del péndulo. El instrumento Von Sterneck, y un instrumento similar desarrollado por Thomas C. Mendenhall de la Costa de los Estados Unidos y la Encuesta Geodésica en 1890, se utilizaron ampliamente para las encuestas en la década de 1920.
- El péndulo de Mendenhall era en realidad un cronómetro más preciso que los relojes de mayor precisión de la época, y como el "mejor reloj del mundo" fue utilizado por Albert A. Michelson en sus mediciones de 1924 de la velocidad de la luz en el monte. Wilson, California.
- Gravímetros de péndulo doble:Comenzando en 1875, la precisión cada vez mayor de las mediciones del péndulo reveló otra fuente de error en los instrumentos existentes: el balanceo del péndulo causó un ligero balanceo del soporte del trípode utilizado para sostener los péndulos portátiles, introduciendo un error. En 1875 Charles S Peirce calculó que las mediciones de la longitud del péndulo de segundos realizadas con el instrumento Repsold requerían una corrección de 0.2 mm debido a este error. En 1880 C. Defforges utilizó un interferómetro de Michelson para medir dinámicamente el balanceo de la plataforma, y se agregaron interferómetros al aparato estándar de Mendenhall para calcular las correcciones de balanceo. Un método para evitar este error fue sugerido por primera vez en 1877 por Hervé Faye y defendido por Peirce, Cellérier y Furtwangler: montar dos péndulos idénticos sobre el mismo soporte, balanceándose con la misma amplitud, 180 ° fuera de fase. El movimiento opuesto de los péndulos cancelaría cualquier fuerza lateral en el soporte. La idea se opuso debido a su complejidad, pero a principios del siglo XX, el dispositivo Von Sterneck y otros instrumentos se modificaron para oscilar múltiples péndulos simultáneamente.
- Gravímetro del Golfo: Uno de los últimos y más precisos gravímetros de péndulo fue el aparato desarrollado en 1929 por Gulf Research and Development Co. Usó dos péndulos de cuarzo fundido, cada uno de 10,7 pulgadas (270 mm) de longitud con un período de 0,89 segundos, oscilando en los pivotes del borde de la cuchilla pyrex, 180 ° fuera de fase. Se montaron en una cámara de vacío con temperatura y humedad permanentemente selladas. Las cargas electrostáticas perdidas en los péndulos de cuarzo tuvieron que ser descargadas al exponerlas a una sal radiactiva antes de su uso. El período se detectó reflejando un haz de luz de un espejo en la parte superior del péndulo, grabado por un registrador de gráficos y comparado con un oscilador de cristal de precisión calibrado contra la señal de tiempo de radio WWV. Este instrumento tenía una precisión de (0.3-0.5) × 10 (30-50 microgals o 3-5 nm / s). Fue utilizado en la década de 1960.
Los gravímetros de péndulo relativos fueron reemplazados por el gravímetro de resorte de longitud cero más simple de LaCoste, inventado en 1934 por Lucien LaCoste. Los gravímetros de péndulo absolutos (reversibles) fueron reemplazados en la década de 1950 por gravímetros de caída libre, en los que se permite que un peso caiga en un tanque de vacío y su aceleración se mide con un interferómetro óptico.
Estándar de longitud
Debido a que la aceleración de la gravedad es constante en un punto dado de la Tierra, el período de un péndulo simple en un lugar determinado depende solo de su longitud. Además, la gravedad varía solo levemente en diferentes lugares. Casi desde el descubrimiento del péndulo hasta principios del siglo XIX, esta propiedad llevó a los científicos a sugerir usar un péndulo de un período dado como un estándar de longitud.
Hasta el siglo XIX, los países basaban sus sistemas de medición de longitud en prototipos, estándares primarios de barra de metal, como el patio estándar en Gran Bretaña mantenido en las Casas del Parlamento, y el estándar toiseen Francia, mantenido en París. Estos eran vulnerables al daño o la destrucción a lo largo de los años, y debido a la dificultad de comparar prototipos, la misma unidad a menudo tenía diferentes longitudes en ciudades distantes, creando oportunidades para el fraude. Durante la Ilustración, los científicos abogaron por un estándar de longitud basado en alguna propiedad de la naturaleza que pudiera determinarse por medición, creando un estándar universal indestructible. El período de péndulos podría medirse con mucha precisión al cronometrarlos con relojes establecidos por las estrellas. Un estándar de péndulo equivalía a definir la unidad de longitud por la fuerza de la gravedad de la Tierra, para todos los intentos constantes, y el segundo, que estaba definido por la velocidad de rotación de la Tierra, también era constante. La idea era que cualquier persona, en cualquier parte de la Tierra,
Prácticamente todas las propuestas se basaron en el péndulo de segundos, en el que cada giro (un medio período) demora un segundo, que es de aproximadamente un metro (39 pulgadas) de largo, porque a fines del siglo XVII se convirtió en un estándar para medir la gravedad (ver sección previa). En el siglo XVIII, su longitud se había medido con precisión submilimétrica en varias ciudades de Europa y el resto del mundo.
La atracción inicial del estándar de longitud del péndulo fue que se creía (por los primeros científicos como Huygens y Wren) que la gravedad era constante sobre la superficie de la Tierra, por lo que un péndulo dado tenía el mismo período en cualquier punto de la Tierra. Por lo tanto, la longitud del péndulo estándar podría medirse en cualquier ubicación y no estaría ligada a ninguna nación o región; sería un estándar verdaderamente democrático y mundial. Aunque Richer descubrió en 1672 que la gravedad varía en diferentes puntos del globo, la idea de un estándar de longitud de péndulo siguió siendo popular, porque se descubrió que la gravedad solo varía con la latitud. La aceleración gravitacional aumenta suavemente desde el ecuador hasta los polos, debido a la forma achatada de la Tierra, por lo que a cualquier latitud dada (línea este-oeste), la gravedad fue lo suficientemente constante como para que la longitud de un péndulo de segundos fuera la misma dentro de la capacidad de medición del siglo XVIII. Por lo tanto, la unidad de longitud podría definirse en una latitud dada y medirse en cualquier punto a lo largo de esa latitud. Por ejemplo, una norma de péndulo definida en 45 ° de latitud norte, una opción popular, podría medirse en partes de Francia, Italia, Croacia, Serbia, Rumania, Rusia, Kazajstán, China, Mongolia, Estados Unidos y Canadá. Además, podría recrearse en cualquier ubicación en la que la aceleración de la gravedad se haya medido con precisión. podría medirse en partes de Francia, Italia, Croacia, Serbia, Rumania, Rusia, Kazajstán, China, Mongolia, Estados Unidos y Canadá. Además, podría recrearse en cualquier ubicación en la que la aceleración de la gravedad se haya medido con precisión. podría medirse en partes de Francia, Italia, Croacia, Serbia, Rumania, Rusia, Kazajstán, China, Mongolia, Estados Unidos y Canadá. Además, podría recrearse en cualquier ubicación en la que la aceleración de la gravedad se haya medido con precisión.
A mediados del siglo XIX, las medidas de péndulo cada vez más precisas de Edward Sabine y Thomas Young revelaron que la gravedad, y por lo tanto la longitud de cualquier estándar de péndulo, variaba mensurablemente con características geológicas locales como montañas y rocas densas del subsuelo. Entonces, un estándar de longitud de péndulo tenía que definirse en un solo punto en la Tierra y solo podía medirse allí. Esto tomó gran parte del atractivo del concepto, y se abandonaron los esfuerzos para adoptar estándares de péndulo.
Propuestas tempranas
Uno de los primeros en sugerir que se definiera la longitud con un péndulo fue el científico flamenco Isaac Beeckman, quien en 1631 recomendó hacer del péndulo de los segundos "la medida invariable para todas las personas en todo momento y lugar". Marin Mersenne, quien midió primero el péndulo de segundos en 1644, también lo sugirió. La primera propuesta oficial para un estándar de péndulo fue hecha por la Royal Society británica en 1660, defendida por Christiaan Huygens y Ole Rømer, basándose en el trabajo de Mersenne, y Huygens en Horologium Oscillatorium propuso un "pie horario" definido como 1/3 del segundos de péndulo. Christopher Wren fue otro partidario temprano. La idea de un estándar de longitud de péndulo debe haber sido familiar para las personas ya en 1663, porque Samuel Butler lo satiriza en Hudibras :
- Sobre el banco los manejaré tan bien
- Que la vibración de este péndulo
- Hará todos los astilleros de un taylor
- Opinión unánime
En 1671, Jean Picard propuso un "pie universal" definido por el péndulo en su influyente Mesure de la Terre . Gabriel Mouton alrededor de 1670 sugirió definir el toise ya sea por un péndulo de segundos o por un minuto de grado terrestre. Un plan para un sistema completo de unidades basado en el péndulo fue avanzado en 1675 por el polímata italiano Tito Livio Burratini. En Francia en 1747, el geógrafo Charles Marie de la Condamine propuso definir la longitud por un péndulo de segundos en el ecuador; ya que en este lugar el giro de un péndulo no se distorsionaría con la rotación de la Tierra. James Steuart (1780) y George Skene Keith también fueron partidarios.
A fines del siglo XVIII, cuando muchas naciones estaban reformando sus sistemas de peso y medida, el péndulo de segundos fue la elección principal para una nueva definición de longitud, defendida por prominentes científicos en varias naciones importantes. En 1790, el entonces secretario de Estado de los Estados Unidos, Thomas Jefferson, propuso al Congreso un "sistema métrico" integral y decimalizado de los Estados Unidos basado en el péndulo de segundos a 38 ° de latitud norte, la latitud media de los Estados Unidos. No se tomó ninguna acción con respecto a esta propuesta. En Gran Bretaña, el principal defensor del péndulo fue el político John Riggs Miller. Cuando sus esfuerzos para promover un sistema métrico conjunto entre el Reino Unido, Francia y los Estados Unidos fracasaron en 1790, propuso un sistema británico basado en la longitud del péndulo de segundos en Londres. Esta norma fue adoptada en 1824 (abajo).
El medidor
En las discusiones previas a la adopción francesa del sistema métrico en 1791, el candidato principal para la definición de la nueva unidad de longitud, el medidor, era el péndulo de segundos a 45 ° de latitud norte. Fue defendido por un grupo dirigido por el político francés Talleyrand y el matemático Antoine Nicolas Caritat de Condorcet. Esta fue una de las tres opciones finales consideradas por el Comité de la Academia Francesa de Ciencias. Sin embargo, el 19 de marzo de 1791 el comité optó por basar el metro en la longitud del meridiano a través de París. Una definición de péndulo fue rechazada debido a su variabilidad en diferentes lugares, y porque definió la longitud por una unidad de tiempo. (Sin embargo, desde 1983, el medidor se ha definido oficialmente en términos de la longitud del segundo y la velocidad de la luz.ancien regime .
Aunque no está definido por el péndulo, la longitud final elegida para el metro, 10 del arco meridiano de polo a ecuador, fue muy cercana a la longitud del péndulo de segundos (0,9937 m), dentro del 0,63%. Aunque no se dio ninguna razón para esta elección en particular en ese momento, fue probablemente para facilitar el uso del péndulo de segundos como un estándar secundario, como se propuso en el documento oficial. Entonces, la unidad de longitud estándar del mundo moderno está estrechamente vinculada históricamente con el péndulo de segundos.
Gran Bretaña y Dinamarca
Gran Bretaña y Dinamarca parecen ser las únicas naciones que (durante un corto tiempo) basaron sus unidades de longitud en el péndulo. En 1821, la pulgada danesa se definió como 1/38 de la longitud del péndulo de segundos solares promedio a 45 ° de latitud en el meridiano de Skagen, al nivel del mar, en el vacío. El parlamento británico aprobó la Ley de Pesos y Medidas Imperialesen 1824, una reforma del sistema estándar británico que declaraba que si se destruía el astillero estándar prototipo, se recuperaría definiendo la pulgada para que la longitud del péndulo de los segundos solares en Londres, a nivel del mar, en el vacío, en 62 ° F fue 39.1393 pulgadas. Esto también se convirtió en el estándar de EE. UU., Ya que en ese momento EE. UU. Usaba medidas británicas. Sin embargo, cuando el patio prototipo se perdió en el incendio de la Cámara de Diputados en 1834, resultó imposible recrearlo con precisión a partir de la definición de péndulo, y en 1855 Gran Bretaña derogó el estándar de péndulo y volvió a los estándares de prototipo.
Otros usos
Seismómetros
Un péndulo en el que la varilla no es vertical, sino casi horizontal, se utilizó en los primeros sismómetros para medir los temblores de tierra. La oscilación del péndulo no se mueve cuando su montaje lo hace, y la diferencia en los movimientos se registra en un cuadro de percusión.
Ajuste de Schuler
Como explicó por primera vez Maximilian Schuler en un artículo de 1923, un péndulo cuyo período es exactamente igual al período orbital de un hipotético satélite que orbita justo sobre la superficie de la tierra (alrededor de 84 minutos) tenderá a permanecer apuntando al centro de la tierra cuando el apoyo se desplaza repentinamente. Este principio, llamado ajuste de Schuler, se usa en sistemas de guía inercial en barcos y aviones que operan en la superficie de la Tierra. No se usa péndulo físico, pero el sistema de control que mantiene estable la plataforma inercial que contiene los giroscopios se modifica para que el dispositivo actúe como si estuviera sujeto a dicho péndulo, manteniendo la plataforma siempre hacia abajo mientras el vehículo se mueve sobre la superficie curva de la tierra.
Péndulos acoplados
En 1665, Huygens hizo una curiosa observación sobre los relojes de péndulo. Se habían colocado dos relojes en su repisa y notó que habían adquirido un movimiento opuesto. Es decir, sus péndulos latían al unísono pero en la dirección opuesta; 180 ° fuera de fase. Independientemente de cómo se iniciaron los dos relojes, descubrió que eventualmente volverían a este estado, y así realizarían la primera observación registrada de un oscilador acoplado.
La causa de este comportamiento fue que los dos péndulos se afectaban entre sí mediante ligeros movimientos de la pieza de soporte. Este proceso se denomina arrastre o bloqueo de modo en la física y se observa en otros osciladores acoplados. Los péndulos sincronizados se han utilizado en relojes y fueron ampliamente utilizados en gravímetros a principios del siglo XX. Aunque Huygens solo observó la sincronización fuera de fase, investigaciones recientes han demostrado la existencia de sincronización en fase, así como estados de "muerte" en los que uno o ambos relojes se detienen.
Práctica religiosa
El movimiento del péndulo también aparece en las ceremonias religiosas. El quemador de incienso oscilante llamado incensario, también conocido como incensario, es un ejemplo de péndulo. Los péndulos también se ven en muchas reuniones en el este de México, donde marcan el cambio de las mareas en el día en que las mareas están en su punto más alto. Ver también péndulos para adivinación y radiestesia.
Educación
Los péndulos son ampliamente utilizados en la educación científica como un ejemplo de un oscilador armónico, para enseñar dinámica y movimiento oscilatorio. Un uso es demostrar la ley de conservación de la energía. Un objeto pesado como una bola de boliche o una bola de demolición se une a una cuerda. Luego, el peso se mueve a unas pocas pulgadas de la cara de un voluntario, luego se libera y se le permite balancearse y regresar. En la mayoría de los casos, el peso invierte la dirección y luego vuelve a (casi) la misma posición que la ubicación de lanzamiento original, es decir, a una pequeña distancia de la cara del voluntario, lo que deja al voluntario ileso. En ocasiones, el voluntario se lesiona si el voluntario no se queda quieto o si el péndulo se suelta inicialmente con un empujón (de modo que cuando vuelve sobrepasa la posición de liberación).
Dispositivo de tortura
Se afirma que el péndulo fue utilizado como instrumento de tortura y ejecución por la Inquisición española en el siglo XVIII. La acusación está contenida en el libro de 1826 La historia de la Inquisición de España escrito por el sacerdote español, historiador y activista liberal Juan Antonio Llorente. Un péndulo oscilante cuyo borde es una hoja de cuchillo desciende lentamente hacia un prisionero atado hasta que corta en su cuerpo. Este método de tortura llegó a la conciencia popular a través del cuento corto de 1842 "El hoyo y el péndulo" del autor estadounidense Edgar Allan Poe, pero existe un considerable escepticismo de que realmente se usó.
La mayoría de las fuentes conocedoras son escépticas de que esta tortura haya sido realmente utilizada. La única evidencia de su uso es un párrafo en el prefacio a la Historia de Llorente de 1826 , que relata un relato de segunda mano de un solo prisionero liberado de la mazmorra de la Inquisición en Madrid en 1820, que supuestamente describió el método de tortura pendular. Las fuentes modernas señalan que debido a la advertencia de Jesús contra el derramamiento de sangre, a los inquisidores solo se les permitía usar métodos de tortura que no derramaran sangre, y el método del péndulo habría violado esta restricción. Una teoría es que Llorente malentendió la cuenta que escuchó; el prisionero se estaba refiriendo a otra tortura común de la Inquisición, el strappado(garrucha), en el cual el prisionero tiene las manos atadas a la espalda y es levantado del piso por una cuerda atada a sus manos. Este método también se conoce como el "péndulo". El popular cuento de terror de Poe y la conciencia pública de los otros métodos brutales de la Inquisición han mantenido vivo el mito de este complicado método de tortura.