Wikiblog Cultulandia [es]

Una proyección bidimensional en perspectiva de una esfera

r - un radio de la esfera, el radio que se encuentra en el centro

Una esfera (del griego σφαῖρα - sphaira , "globo, bola") es un objeto geométrico perfectamente redondo en el espacio tridimensional que es la superficie de una bola completamente redonda (a saber, análoga a los objetos circulares en dos dimensiones, donde "círculo" circunscribe su "disco").

Al igual que un círculo en un espacio bidimensional, una esfera se define matemáticamente como el conjunto de puntos que están todos a la misma distancia

r

de un punto dado, pero en un espacio tridimensional. Esta distancia

r

es el radio de la pelota, que se compone de todos los puntos con una distancia inferior a

r

desde el punto dado, que es el centro de la bola matemática. Estos también se conocen como el radio y el centro de la esfera, respectivamente. La línea recta más larga a través de la bola, conectando dos puntos de la esfera, pasa a través del centro y su longitud es, por lo tanto, dos veces el radio; es un diámetro de la esfera y su bola.

Mientras que fuera de las matemáticas, los términos "esfera" y "bola" a veces se usan indistintamente, en matemáticas la distinción anterior se hace entre una esfera , que es una superficie cerrada bidimensional, incrustada en un espacio euclidiano tridimensional, y una bola , que es una forma tridimensional que incluye la esfera y todo dentro de la esfera (una bola cerrada ), o, más a menudo, solo los puntos dentro , pero no en la esfera (una bola abierta) Esta distinción no siempre se ha mantenido y, especialmente, las referencias matemáticas más antiguas hablan de una esfera como un sólido. Esto es análogo a la situación en el avión, donde los términos "círculo" y "disco" también pueden confundirse.

Ecuaciones en el espacio tridimensional

En geometría analítica, una esfera con centro

(x 0, y 0, z 0)

y radio

r

es el lugar geométrico de todos los puntos

(x, y, z)

tal que

{\ displaystyle (x-x_ {0}) ^ {2} + (y-y_ {0}) ^ {2} + (z-z_ {0}) ^ {2} = r ^ {2}.}

Deje

a, b, c, d, e

ser números reales con

un \neq 0

y poner

{\ displaystyle x_ {0} = {\ frac {-b} {a}}, \ quad y_ {0} = {\ frac {-c} {a}}, \ quad z_ {0} = {\ frac { -d} {a}}, \ quad \ rho = {\ frac {b ^ {2} + c ^ {2} + d ^ {2} -ae} {a ^ {2}}}.}

Entonces la ecuación

{\ displaystyle f (x, y, z) = a (x ^ {2} + y ^ {2} + z ^ {2}) + 2 (bx + cy + dz) + e = 0}

no tiene puntos reales como soluciones si y se llama ecuación de una esfera imaginaria . Si la única solución de es el punto y la ecuación se dice que es la ecuación de una esfera de puntos . Finalmente, en el caso , es una ecuación de una esfera cuyo centro es y cuyo radio es .

\ rho <0

\ rho = 0

{\ displaystyle f (x, y, z) = 0}

P_ {0} = (x_ {0}, y_ {0}, z_ {0})

\ rho> 0

{\ displaystyle f (x, y, z) = 0}

P_ {0}

{\ displaystyle {\ sqrt {\ rho}}}

Si

a

en la ecuación anterior es cero, entonces

f (x, y, z) = 0

es la ecuación de un plano. Por lo tanto, se puede pensar que un plano es una esfera de radio infinito cuyo centro es un punto en el infinito.

Los puntos en la esfera con radio y centro se pueden parametrizar a través de

r> 0

(x_ {0}, y_ {0}, z_ {0})

{\ displaystyle {\ begin {aligned} x & = x_ {0} + r \ sin \ varphi \; \ cos \ theta \\ y & yy {0} + r \ sin \ varphi \; \ sin \ theta \ qquad ( - {\ pi} / 2 \ leq \ varphi \ leq {\ pi} / 2, \; 0 \ leq \ theta <2 \ pi) \\ z & = z_ {0} + r \ cos \ varphi \, \ end {alineado}}}

Una esfera de cualquier radio centrada en cero es una superficie integral de la siguiente forma diferencial:

{\ displaystyle x \, dx + y \, dy + z \, dz = 0.}

Esta ecuación refleja que los vectores de posición y velocidad de un punto,

(x, y, z)

y

(dx, dy, dz)

, que viajan en la esfera son siempre ortogonales entre sí.

También se puede construir una esfera como la superficie formada al rotar un círculo alrededor de cualquiera de sus diámetros. Como un círculo es un tipo especial de elipse, una esfera es un tipo especial de elipsoide de revolución. Al reemplazar el círculo con una elipse girada alrededor de su eje mayor, la forma se convierte en un esferoide prolato; rotado sobre el eje menor, un esferoide achatado.

Volumen cerrado

Cilindro circunscrito a una esfera

En tres dimensiones, el volumen dentro de una esfera (que es el volumen de una bola) es

V = \ frac {4} {3} \ pi r ^ 3

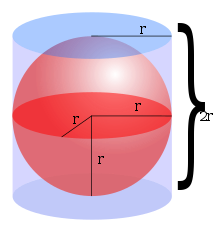
donde

r

es el radio de la esfera. Arquímedes primero obtuvo esta fórmula, al mostrar que el volumen dentro de una esfera es dos veces la diferencia en los volúmenes entre el interior de una esfera y el interior de un cilindro circunscrito (que tiene la altura y el diámetro igual al diámetro de la esfera). Esta afirmación puede obtenerse del principio de Cavalieri. Esta fórmula también se puede derivar usando el cálculo integral, es decir, la integración de disco para sumar los volúmenes de un número infinito de discos circulares de infinitesimalmente pequeño lado apilados espesor a lado y centrada a lo largo de la

x

eje x de

x = - r

a

x = r

, suponiendo la esfera de radio

r

está centrado en el origen.

En cualquier

x

dada , el volumen incremental (

δV

) es igual al producto del área de la sección transversal del disco en

xy

su grosor (

δx

):

{\ displaystyle \ delta V \ approx \ pi y ^ {2} \ cdot \ delta x.}

El volumen total es la suma de todos los volúmenes incrementales:

{\ displaystyle V \ approx \ sum \ pi y ^ {2} \ cdot \ delta x.}

En el límite cuando

δx se

acerca a cero, esta ecuación se convierte en:

{\ displaystyle V = \ int _ {- r} ^ {r} \ pi y ^ {2} dx.}

En cualquier

x

dada , un triángulo rectángulo conecta

x

,

y

y

r

al origen; por lo tanto, aplicando el teorema de Pitágoras rinde:

{\ displaystyle y ^ {2} = r ^ {2} -x ^ {2}.}

Usando esta sustitución da

{\ displaystyle V = \ int _ {- r} ^ {r} \ pi (r ^ {2} -x ^ {2}) dx,}

que se puede evaluar para dar el resultado

{\ displaystyle V = \ pi \ left [r ^ {2} x - {\ frac {x ^ {3}} {3}} \ right] _ {- r} ^ {r} = \ pi \ left (r ^ {3} - {\ frac {r ^ {3}} {3}} \ right) - \ pi \ left (-r ^ {3} + {\ frac {r ^ {3}} {3}} \ derecha) = {\ frac {4} {3}} \ pi r ^ {3}.}

Alternativamente, esta fórmula se encuentra usando coordenadas esféricas, con elemento de volumen

{\ displaystyle dV = r ^ {2} \ sin \ theta \, dr \, d \ theta \, d \ varphi}

asi que

{\ displaystyle V = \ int _ {0} ^ {2 \ pi} \ int _ {0} ^ {\ pi} \ int _ {0} ^ {r} r '^ {2} \ sin \ theta \, dr '\, d \ theta \, d \ varphi = 2 \ pi \ int _ {0} ^ {\ pi} \ int _ {0} ^ {r} r' ^ {2} \ sin \ theta \, dr '\, d \ theta = 4 \ pi \ int _ {0} ^ {r} r' ^ {2} \, dr '\ = {\ frac {4} {3}} \ pi r ^ {3}. }

Para la mayoría de los propósitos prácticos, el volumen dentro de una esfera inscrita en un cubo puede aproximarse al 52.4% del volumen del cubo, ya que

V = π / 6 d

, donde

d

es el diámetro de la esfera y también la longitud de un lado del cubo y

π

/6 ≈ 0.5236. Por ejemplo, una esfera con un diámetro de 1 metro tiene un 52,4% del volumen de un cubo con una longitud de borde de 1 metro, o aproximadamente 0,524 m.

Área de superficie

El área de superficie de una esfera de radio

r

es:

A = 4 \ pi r ^ {2}.

Arquímedes primero derivó esta fórmula del hecho de que la proyección a la superficie lateral de un cilindro circunscrito preserva el área. Otro enfoque para obtener la fórmula proviene del hecho de que es igual a la derivada de la fórmula para el volumen con respecto a

r

porque el volumen total dentro de una esfera de radio

r

puede considerarse la suma del área superficial de un número infinito de capas esféricas de espesor infinitesimal apiladas concéntricamente una dentro de la otra desde el radio 0 al radio

r

. A un grosor infinitesimal, la discrepancia entre el área de superficie interna y externa de cualquier caparazón dado es infinitesimal, y el volumen elemental en el radio

r

es simplemente el producto del área superficial en el radio

r

y el grosor infinitesimal.

En cualquier radio dado

r

, el volumen incremental (

δV

) es igual al producto del área superficial en el radio

r

(

A (r)

) y el grosor de un caparazón (

δr

):

\ delta V \ approx A (r) \ cdot \ delta r.

El volumen total es la suma de todos los volúmenes de shell:

V \ approx \ sum A (r) \ cdot \ delta r.

En el límite cuando

δr se

aproxima a cero, esta ecuación se convierte en:

V = \ int _ {0} ^ {r} A (r) \, dr.

Sustituto

V

:

{\ displaystyle {\ frac {4} {3}} \ pi r ^ {3} = \ int _ {0} ^ {r} A (r) \, dr.}

La diferenciación de ambos lados de esta ecuación con respecto a

r

produce

A

en función de

r

:

{\ displaystyle 4 \ pi r ^ {2} = A (r).}

Esto generalmente se abrevia como:

A = 4 \ pi r ^ {2},

donde

r

ahora se considera que es el radio fijo de la esfera.

Alternativamente, el elemento de área en la esfera se da en coordenadas esféricas mediante

dA = r sen θ dθ dφ

. En coordenadas cartesianas, el elemento de área es

{\ displaystyle dS = {\ frac {r} {\ sqrt {r ^ {2} - {\ displaystyle \ sum _ {i \ neq k} x_ {i} ^ {2}}}}} \ prod _ {i \ neq k} dx_ {i}, \; \ forall k.}

Para mayor generalidad, vea el elemento de área.

El área total puede así obtenerse por integración:

A = \ int _ {0} ^ {2 \ pi} \ int _ {0} ^ {\ pi} r ^ {2} \ sin \ theta \, d \ theta \, d \ varphi = 4 \ pi r ^ {2}

Una imagen de una de las esferas más precisas hechas por el hombre, ya que refracta la imagen de Einstein en el fondo. Esta esfera era un cuarzigroscopio fundido para Gravity Probe Bexperiment, y difiere en forma de una esfera perfecta en no más de 40 átomos (menos de 10 nanómetros) de grosor. Se anunció el 1 de julio de 2008 que los científicos australianos habían creado esferas aún más perfectas, con una precisión de 0.3 nanómetros, como parte de una búsqueda internacional para encontrar un nuevo kilogramo estándar mundial.

La esfera tiene el área superficial más pequeña de todas las superficies que encierran un volumen dado, y encierra el mayor volumen entre todas las superficies cerradas con un área superficial determinada. Por lo tanto, la esfera aparece en la naturaleza: por ejemplo, las burbujas y las pequeñas gotas de agua son aproximadamente esféricas porque la tensión superficial minimiza localmente el área superficial.

El área de superficie relativa a la masa de una bola se denomina área de superficie específica y puede expresarse a partir de las ecuaciones indicadas anteriormente como

{\ displaystyle \ mathrm {SSA} = {\ frac {A} {V \ rho}} = {\ frac {3} {r \ rho}},}

donde

ρ

es la densidad (la relación de masa a volumen).

Propiedades geométricas

Una esfera está determinada únicamente por cuatro puntos que no son coplanarios. De manera más general, una esfera está determinada de forma única por cuatro condiciones, como pasar por un punto, ser tangente a un plano, etc. Esta propiedad es análoga a la propiedad de que tres puntos no colineales determinan un círculo único en un plano.

En consecuencia, una esfera está determinada de manera única por (es decir, atraviesa) un círculo y un punto que no está en el plano de ese círculo.

Al examinar las soluciones comunes de las ecuaciones de dos esferas, se puede ver que dos esferas se cruzan en un círculo y el plano que contiene ese círculo se llama plano radical de las esferas que se cruzan. Aunque el plano radical es un plano real, el círculo puede ser imaginario (las esferas no tienen ningún punto real en común) o consistir en un solo punto (las esferas son tangentes en ese punto).

El ángulo entre dos esferas en un punto real de intersección es el ángulo diedro determinado por los planos tangentes a las esferas en ese punto. Dos esferas se intersectan en el mismo ángulo en todos los puntos de su círculo de intersección. Se cruzan en ángulos rectos (son ortogonales) si y solo si los cuadrados de la distancia entre sus centros es igual a la suma de los cuadrados de sus radios.

Lápiz de esferas

Si

f (x, y, z) = 0

y

g (x, y, z) = 0

son las ecuaciones de dos esferas distintas entonces

{\ displaystyle sf (x, y, z) + tg (x, y, z) = 0}

es también la ecuación de una esfera para valores arbitrarios de los parámetros

s

y

t

. El conjunto de todas las esferas que satisfacen esta ecuación se llama un lapiz de esferas determinado por las dos esferas originales. En esta definición, se permite que una esfera sea un plano (radio infinito, centro en el infinito) y si ambas esferas originales son planos, entonces todas las esferas del lápiz son planos; de lo contrario, hay un solo plano (el plano radical) en el lápiz.

Si el lápiz de esferas no consiste en todos los planos, entonces hay tres tipos de lápices:

Si las esferas se intersectan en un círculo real $C$ , entonces el lápiz está formado por todas las esferas que contienen $C$ , incluido el plano radical. Los centros de todas las esferas ordinarias en el lápiz se encuentran en una línea que pasa por el centro de $C$ y perpendicular al plano radical.
Si las esferas se intersectan en un círculo imaginario, todas las esferas del lápiz también pasan a través de este círculo imaginario, pero como esferas ordinarias son disjuntas (no tienen puntos reales en común). La línea de centros es perpendicular al plano radical, que es un plano real en el lápiz que contiene el círculo imaginario.
Si las esferas se intersectan en un punto $A$ , todas las esferas del lápiz son tangentes en $A$ y el plano radical es el plano tangente común de todas estas esferas. La línea de centros es perpendicular al plano radical en $A$ .

Todas las líneas tangentes desde un punto fijo del plano radical hasta las esferas de un lápiz tienen la misma longitud.

El plano radical es el lugar de los centros de todas las esferas que son ortogonales a todas las esferas de un lápiz. Además, una esfera ortogonal a dos esferas cualquiera de un lápiz de esferas es ortogonal a todas ellas y su centro se encuentra en el plano radical del lápiz.

Terminología

Los pares de puntos en una esfera que se encuentran en una línea recta a través del centro de la esfera se llaman puntos antipodales. Un gran círculo es un círculo en la esfera que tiene el mismo centro y radio que la esfera y, en consecuencia, lo divide en dos partes iguales. Las secciones planas de una esfera se llaman secciones esféricas . Todos son círculos y aquellos que no son círculos grandes se llaman círculos pequeños .

La distancia más corta a lo largo de la superficie entre dos puntos no antípodas distintos en la esfera es la longitud del arco más pequeño de los dos en el gran círculo único que incluye los dos puntos. Equipado con esta "distancia de gran círculo", un gran círculo se convierte en el círculo de Riemann.

Si un punto particular en una esfera se designa (arbitrariamente) como su polo norte , entonces el punto antípoda correspondiente se llama polo sur , y el ecuador es el gran círculo que es equidistante a ellos. Los grandes círculos a través de los dos polos se llaman líneas (o meridianos) de longitud, y la línea que conecta los dos polos se denomina eje de rotación. Los círculos en la esfera que son paralelos al ecuador son líneas de latitud. Esta terminología también se usa para cuerpos astronómicos aproximadamente esferoidales como el planeta Tierra (ver geoide).

Hemisferio

Cualquier plano que incluya el centro de una esfera lo divide en dos hemisferios iguales . Cualquiera de los dos planos que se cruzan que incluyen el centro de una esfera subdividen la esfera en cuatro lunes o biangles, cuyos vértices coinciden todos con los puntos antípoda que se encuentran en la línea de intersección de los planos.

El cociente antípoda de la esfera es la superficie llamada el plano proyectivo real, que también se puede considerar como el hemisferio norte con puntos antípodas del ecuador identificados.

Se conjetura que el hemisferio es el relleno isométrico óptimo (área mínima) del círculo de Riemann.

Generalizaciones

Dimensionalidad

Las esferas se pueden generalizar a espacios de cualquier cantidad de dimensiones. Para cualquier número natural

n

, una "

n

-esfera", a menudo escrita como

S

, es el conjunto de puntos en el espacio euclidiano (

n + 1

) -dimensional que están a una distancia fija

r

de un punto central de ese espacio, donde

r

es, como antes, un número real positivo. En particular:

$S$ : una esfera 0 es un par de puntos finales de un intervalo $[- r, r$ de la línea real
$S$ : una 1 esfera es un círculo de radio r
$S$ : una 2-esfera es una esfera ordinaria
$S$ : una esfera de 3 es una esfera en espacio euclidiano de 4 dimensiones.

Las esferas para

n > 2 a

veces se llaman hiperesferas.

La

n

-esfera del radio de la unidad centrada en el origen se denota

S

y a menudo se denomina "la"

n

-esfera. Tenga en cuenta que la esfera ordinaria es una 2-esfera, porque es una superficie bidimensional (que está incrustada en el espacio tridimensional).

El área de superficie de la unidad (

n -1

) -esfera es

{\ displaystyle {\ frac {2 \ pi ^ {\ frac {n} {2}}} {\ Gamma \ left ({\ frac {n} {2}} \ right)}}}

donde

Γ (z)

es la función gamma de Euler.

Otra expresión para el área de superficie es

{\ displaystyle {\ begin {cases} \ displaystyle {\ frac {(2 \ pi) ^ {n / 2} \, r ^ {n-1}} {2 \ cdot 4 \ cdots (n-2)}} , & {\ text {if}} n {\ text {es par}}; \\\\\ displaystyle {\ frac {2 (2 \ pi) ^ {(n-1) / 2} \, r ^ { n-1}} {1 \ cdot 3 \ cdots (n-2)}}, & {\ text {if}} n {\ text {es impar}}. \ end {cases}}}

y el volumen es el área de superficie multiplicado por

r / n

o

{\ displaystyle {\ begin {cases} \ displaystyle {\ frac {(2 \ pi) ^ {n / 2} \, r ^ {n}} {2 \ cdot 4 \ cdots n}}, & {\ text { if}} n {\ text {is even}}; \\\\\ displaystyle {\ frac {2 (2 \ pi) ^ {(n-1) / 2} \, r ^ {n}} {1 \ cdot 3 \ cdots n}}, & {\ text {if}} n {\ text {es impar}}. \ end {cases}}}

También existen fórmulas recursivas generales para el volumen de una bola

n

.

Espacios métricos

De manera más general, en un espacio métrico

(E, d)

, la esfera del centro

xy el

radio

r > 0

es el conjunto de puntos

y

tal que

d (x, y) = r

.

Si el centro es un punto distinguido que se considera el origen de

E

, como en un espacio normativo, no se menciona en la definición ni en la notación. Lo mismo aplica para el radio si se toma para igualar uno, como en el caso de una esfera de unidad.

A diferencia de una pelota, incluso una esfera grande puede ser un juego vacío. Por ejemplo, en

Z

con métrica euclidiana, una esfera de radio

r

es no vacía solo si

r

puede escribirse como suma de

n

cuadrados de enteros.

Topología

En topología, una

n

-esfera se define como un espacio homeomórfico al límite de una

bola

(n + 1)

; por lo tanto, es homeomorfo al euclidiano

n

-sphere, pero quizás carece de su métrica.

Una esfera 0 es un par de puntos con la topología discreta.
Una 1 esfera es un círculo (hasta el homeomorfismo); así, por ejemplo, (la imagen de) cualquier nudo es una 1 esfera.
Una esfera de 2 es una esfera ordinaria (hasta el homeomorfismo); así, por ejemplo, cualquier esferoide es una 2-esfera.

El

n

-sphere se denota

S

. Es un ejemplo de una variedad topológica compacta sin límite. Una esfera no necesita ser lisa; si es suave, no tiene que ser diferente a la esfera euclidiana.

El teorema de Heine-Borel implica que una esfera-

n

euclidiana es compacta. La esfera es la imagen inversa de un conjunto de un punto bajo la función continua

|| x ||

. Por lo tanto, la esfera está cerrada.

S

también está limitado; por lo tanto, es compacto.

Sorprendentemente, es posible convertir una esfera común de adentro hacia afuera en un espacio tridimensional con posibles autointersecciones, pero sin crear ningún pliegue, en un proceso llamado eversión de esfera.

Geometría esférica

Gran círculo en una esfera

Los elementos básicos de la geometría del plano euclidiano son puntos y líneas. En la esfera, los puntos se definen en el sentido habitual. El análogo de la "línea" es la geodésica, que es un gran círculo; la característica definitoria de un gran círculo es que el plano que contiene todos sus puntos también pasa por el centro de la esfera. La medición por longitud de arco muestra que el camino más corto entre dos puntos que se encuentran en la esfera es el segmento más corto del gran círculo que incluye los puntos.

Muchos teoremas de la geometría clásica también son válidos para la geometría esférica, pero no todos lo hacen porque la esfera no satisface algunos de los postulados de la geometría clásica, incluido el postulado paralelo. En la trigonometría esférica, los ángulos se definen entre los círculos grandes. La trigonometría esférica difiere de la trigonometría ordinaria en muchos aspectos. Por ejemplo, la suma de los ángulos interiores de un triángulo esférico siempre excede 180 grados. Además, dos triángulos esféricos similares son congruentes.

Once propiedades de la esfera

Un vector normal para una esfera, un plano normal y su sección normal. La curvatura de la curva de intersección es la curvatura seccional. Para la esfera, cada sección normal a través de un punto dado será un círculo del mismo radio: el radio de la esfera. Esto significa que cada punto en la esfera será un punto umbilical.

En su libro Geometry and the Imagination, David Hilbert y Stephan Cohn-Vossen describen once propiedades de la esfera y discuten si estas propiedades determinan de manera única la esfera. Varias propiedades son válidas para el avión, que se puede considerar como una esfera con radio infinito. Estas propiedades son:

Los puntos en la esfera están todos a la misma distancia de un punto fijo. Además, la relación de la distancia de sus puntos desde dos puntos fijos es constante.

La primera parte es la definición habitual de la esfera y la determina de manera única. La segunda parte se puede deducir fácilmente y sigue un resultado similar de Apolonio de Perga para el círculo. Esta segunda parte también es válida para el avión.

Los contornos y las secciones planas de la esfera son círculos.

Esta propiedad define la esfera de forma única.

La esfera tiene un ancho constante y una circunferencia constante.

El ancho de una superficie es la distancia entre pares de planos tangentes paralelos. Numerosas otras superficies convexas cerradas tienen un ancho constante, por ejemplo, el cuerpo Meissner. La circunferencia de una superficie es la circunferencia del límite de su proyección ortogonal sobre un plano. Cada una de estas propiedades implica la otra.

Todos los puntos de una esfera son umbilicales.

En cualquier punto de una superficie, una dirección normal está en ángulo recto con la superficie porque la esfera es la línea que se irradia desde el centro de la esfera. La intersección de un plano que contiene la normal con la superficie formará una curva que se llama sección normal, y la curvatura de esta curva es la curvatura normal . Para la mayoría de los puntos en la mayoría de las superficies, las diferentes secciones tendrán diferentes curvaturas; los valores máximo y mínimo de estos se llaman las curvaturas principales. Cualquier superficie cerrada tendrá al menos cuatro puntos llamados puntos umbilicales. En un umbilical todas las curvaturas seccionales son iguales; en particular las curvaturas principales son iguales. Los puntos umbilicales se pueden considerar como los puntos en los que la superficie se aproxima mucho a una esfera.
Para la esfera, las curvaturas de todas las secciones normales son iguales, por lo que cada punto es un umbilical. La esfera y el plano son las únicas superficies con esta propiedad.

La esfera no tiene una superficie de centros.
Para una sección normal dada existe un círculo de curvatura que es igual a la curvatura seccional, es tangente a la superficie, y las líneas centrales de las cuales se encuentran a lo largo de la línea normal. Por ejemplo, los dos centros correspondientes a las curvaturas seccionales máximas y mínimas se denominan puntos focales , y el conjunto de todos esos centros forma la superficie focal.
Para la mayoría de las superficies, la superficie focal forma dos hojas que son cada una una superficie y se encuentran en los puntos umbilicales. Varios casos son especiales:
- Para las superficies del canal, una hoja forma una curva y la otra hoja es una superficie
- Para conos, cilindros, toros y ciclidos ambas hojas forman curvas.
- Para la esfera, el centro de cada círculo osculante está en el centro de la esfera y la superficie focal forma un solo punto. Esta propiedad es exclusiva de la esfera.

Todas las geodésicas de la esfera son curvas cerradas.

Las geodésicas son curvas en una superficie que dan la distancia más corta entre dos puntos. Son una generalización del concepto de una línea recta en el plano. Para la esfera, las geodésicas son círculos grandiosos. Muchas otras superficies comparten esta propiedad.

De todos los sólidos que tienen un volumen dado, la esfera es la que tiene la superficie más pequeña; de todos los sólidos que tienen una superficie específica dada, la esfera es la que tiene el mayor volumen.

Se sigue de la desigualdad isoperimétrica. Estas propiedades definen la esfera de manera única y se puede ver en las burbujas de jabón: una burbuja de jabón encierra un volumen fijo, y la tensión superficial minimiza su área de superficie para ese volumen. Por lo tanto, una burbuja de jabón flotante se aproxima a una esfera (aunque fuerzas externas como la gravedad distorsionarán ligeramente la forma de la burbuja).

La esfera tiene la curvatura media total más pequeña entre todos los sólidos convexos con un área superficial determinada.

La curvatura media es el promedio de las dos curvaturas principales, que es constante porque las dos curvaturas principales son constantes en todos los puntos de la esfera.

La esfera tiene una curvatura media constante.

La esfera es la única superficie incrustada que carece de límites o singularidades con curvatura media positiva constante. Otras superficies sumergidas tales como superficies mínimas tienen una curvatura media constante.

La esfera tiene una curvatura gaussiana positiva constante.

La curvatura gaussiana es el producto de las dos curvaturas principales. Es una propiedad intrínseca que se puede determinar midiendo la longitud y los ángulos, y es independiente de cómo la superficie está incrustada en el espacio. Por lo tanto, doblar una superficie no alterará la curvatura gaussiana, y otras superficies con curvatura gaussiana positiva constante se pueden obtener cortando una pequeña ranura en la esfera y doblándola. Todas estas otras superficies tendrían límites, y la esfera es la única superficie que carece de un límite con una curvatura Gaussiana constante y positiva. La pseudoesfera es un ejemplo de una superficie con curvatura gaussiana negativa constante.

La esfera se transforma en sí misma por una familia de tres parámetros de movimientos rígidos.

Al girar alrededor de cualquier eje, una unidad de esfera en el origen mapeará la esfera sobre sí misma. Cualquier rotación alrededor de una línea a través del origen se puede expresar como una combinación de rotaciones alrededor del eje de tres coordenadas (ver ángulos de Euler). Por lo tanto, existe una familia de rotaciones de tres parámetros tal que cada rotación transforma la esfera sobre sí misma; esta familia es el grupo de rotación SO (3). El avión es la única otra superficie con una familia de tres parámetros de transformaciones (traducciones a lo largo de la $x$ - y $Y$ -axes y rotaciones alrededor del origen). Los cilindros circulares son las únicas superficies con familias de dos parámetros de movimientos rígidos y las superficies de revolución y helicoides son las únicas superficies con una familia de un solo parámetro.

Buscar en este blog

Wikiblog Cultulandia [es]

Esfera

Esfera

Definición

Ecuaciones en el espacio tridimensional

Volumen cerrado

Área de superficie

Propiedades geométricas

Lápiz de esferas

Terminología

Hemisferio

Generalizaciones

Dimensionalidad

Espacios métricos

Topología

Geometría esférica

Once propiedades de la esfera

Contenidos Relacionados de Matemáticas ››