Wikiblog Cultulandia [es]

Área
Símbolos comunes	UN
Unidad SI	Metro cuadrado [m]
En unidades base SI	1 m

El área combinada de estas tres formas es de aproximadamente 15.57 cuadrados.

Área es la cantidad que expresa la extensión de una figura o forma bidimensional, o lámina plana, en el plano. El área de la superficie es su análogo en la superficie bidimensional de un objeto tridimensional. El área se puede entender como la cantidad de material con un grosor dado que sería necesario para configurar un modelo de la forma, o la cantidad de pintura necesaria para cubrir la superficie con una sola capa. Es el análogo bidimensional de la longitud de una curva (un concepto unidimensional) o el volumen de un sólido (un concepto tridimensional).

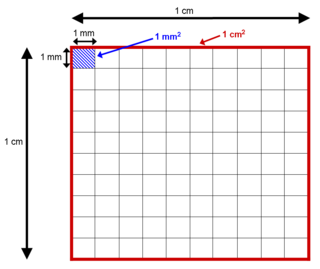
El área de una forma se puede medir comparando la forma con cuadrados de un tamaño fijo. En el Sistema Internacional de Unidades (SI), la unidad de área estándar es el metro cuadrado (escrito como m), que es el área de un cuadrado cuyos lados tienen un metro de largo. Una forma con un área de tres metros cuadrados tendría la misma área que tres de esos cuadrados. En matemáticas, el cuadrado de la unidad se define para tener el área uno, y el área de cualquier otra forma o superficie es un número real adimensional.

Existen varias fórmulas bien conocidas para las áreas de formas simples como triángulos, rectángulos y círculos. Usando estas fórmulas, el área de cualquier polígono se puede encontrar dividiendo el polígono en triángulos. Para las formas con el límite curvo, generalmente se requiere cálculo para calcular el área. De hecho, el problema de determinar el área de las figuras planas fue una gran motivación para el desarrollo histórico del cálculo.

Para una forma sólida, como una esfera, cono o cilindro, el área de su superficie límite se denomina área de superficie. Las fórmulas para las áreas superficiales de formas simples fueron calculadas por los antiguos griegos, pero calcular el área de la superficie de una forma más complicada generalmente requiere cálculo multivariable.

El área juega un papel importante en las matemáticas modernas. Además de su importancia obvia en geometría y cálculo, el área se relaciona con la definición de determinantes en el álgebra lineal, y es una propiedad básica de las superficies en geometría diferencial. En el análisis, el área de un subconjunto del plano se define utilizando la medida de Lebesgue, aunque no todos los subconjuntos son medibles. En general, el área en matemáticas superiores se ve como un caso especial de volumen para regiones bidimensionales.

El área puede definirse mediante el uso de axiomas, definiéndolo como una función de una colección de ciertas figuras planas para el conjunto de números reales. Se puede demostrar que tal función existe.

Definicion formal

Un enfoque para definir lo que significa "área" es a través de axiomas. "Área" se puede definir como una función de una colección M de tipo especial de figuras planas (denominadas conjuntos medibles) al conjunto de números reales que cumple las siguientes propiedades:

Para todo S en M , a ( S ) ≥ 0.
Si S y T están en M entonces también lo son S ∪ T y S ∩ T , y también a ( S ∪ T ) = a ( S) + a ( T ) - a ( S ∩ T ).
Si S y T están en M con S ⊆ T entonces T - S está en M y a ( T - S ) = a ( T ) - a ( S ).
Si un conjunto S está en M y S es congruente con T, entonces T también está en M y a ( S ) = a ( T ).
Cada rectángulo R está en M . Si el rectángulo tiene la longitud hy la anchura k, entonces a ( R ) = hk .
Deje que Q sea un conjunto cerrado entre dos regiones de paso S y T . Una región paso está formado por una unión finita de rectángulos adyacentes que descansan sobre una base común, es decir, S ⊆ Q ⊆ T . Si hay un número único c tal que a ( S ) ≤ c ≤ a ( T ) para todas las regiones de paso S y T , entonces a ( Q ) = c .

Se puede demostrar que tal función de área realmente existe.

Unidades

Un cuadrado hecho de tubería de PVC sobre hierba

Un cuadrante cuadrado hecho de tubo de PVC.

Cada unidad de longitud tiene una unidad de área correspondiente, es decir, el área de un cuadrado con la longitud del lado dado. Así las áreas se pueden medir en metros cuadrados (m), centímetros cuadrados (cm), milímetros cuadrados (mm), kilómetros cuadrados (km), pies cuadrados (pies), yardas cuadradas (yardas), millas cuadradas (millas), y así adelante. Algebraicamente, estas unidades pueden considerarse como los cuadrados de las unidades de longitud correspondientes.

La unidad de área SI es el metro cuadrado, que se considera una unidad derivada de SI.

Conversiones

Aunque hay 10 mm en 1 cm, hay 100 mm en 1 cm.

El cálculo del área de un cuadrado cuya longitud y ancho son de 1 metro sería:

1 metro x 1 metro = 1 m

y así, un rectángulo con lados diferentes (digamos una longitud de 3 metros y un ancho de 2 metros) tendría un área en unidades cuadradas que se puede calcular como:

3 metros x 2 metros = 6 m. Esto es equivalente a 6 millones de milímetros cuadrados. Otras conversiones útiles son:

1 kilómetro cuadrado = 1,000,000 de metros cuadrados
1 metro cuadrado = 10,000 centímetros cuadrados = 1,000,000 de milímetros cuadrados
1 centímetro cuadrado = 100 milímetros cuadrados.

Unidades no métricas

En unidades no métricas, la conversión entre dos unidades cuadradas es el cuadrado de la conversión entre las unidades de longitud correspondientes.

1 pie = 12 pulgadas,

la relación entre pies cuadrados y pulgadas cuadradas es

1 pie cuadrado = 144 pulgadas cuadradas,

donde 144 = 12 = 12 × 12. Del mismo modo:

1 yarda cuadrada = 9 pies cuadrados
1 milla cuadrada = 3,097,600 yardas cuadradas = 27,878,400 pies cuadrados

Además, los factores de conversión incluyen:

1 pulgada cuadrada = 6.4516 centímetros cuadrados
1 pie cuadrado = 0.092 903 04 metros cuadrados
1 yarda cuadrada = 0.836 127 36 metros cuadrados
1 milla cuadrada = 2.589 988 110 336 kilómetros cuadrados

Otras unidades incluyendo histórica

Hay varias otras unidades comunes para el área. The are era la unidad original de área en el sistema métrico, con:

1 es = 100 metros cuadrados

Aunque el han caído fuera de uso, la hectárea todavía se usa comúnmente para medir la tierra:

1 hectárea = 100 hectáreas = 10,000 metros cuadrados = 0.01 kilómetros cuadrados

Otras unidades métricas de área poco comunes incluyen la tétrada, la hectárea y la miríada.

El acre también se usa comúnmente para medir áreas terrestres, donde

1 acre = 4,840 yardas cuadradas = 43,560 pies cuadrados.

Un acre es aproximadamente 40% de una hectárea.

En la escala atómica, el área se mide en unidades de graneros, de modo que:

1 granero = 10 metros cuadrados.

El granero se usa comúnmente para describir el área de interacción transversal en física nuclear.

En India,

20 dhurki = 1 dhur
20 dhur = 1 khatha
20 khata = 1 bigha
32 khata = 1 acre

Historia

Área del círculo

En el siglo V aC, Hipócrates de Quíos fue el primero en mostrar que el área de un disco (la región encerrada por un círculo) es proporcional al cuadrado de su diámetro, como parte de su cuadratura de la lune de Hipócrates, pero no lo hizo identifica la constante de proporcionalidad. Eudoxo de Cnido, también en el siglo V aC, también descubrió que el área de un disco es proporcional a su radio al cuadrado.

Posteriormente, el Libro I de los Elementos de Euclides trató la igualdad de áreas entre figuras bidimensionales. El matemático Arquímedes utilizó las herramientas de la geometría euclidiana para mostrar que el área dentro de un círculo es igual a la de un triángulo rectángulo cuya base tiene la longitud de la circunferencia del círculo y cuya altura es igual al radio del círculo, en su libro Medición de un círculo . (La circunferencia es 2

π

r , y el área de un triángulo es la mitad de la base multiplicada por la altura, lo que da lugar al área

π

r para el disco.) Arquímedes aproximó el valor de π (y de ahí el área de un círculo de radio de unidad) con su método de doblar, en el cual inscribió un triángulo regular en un círculo y anotó su área, luego duplicó el número de lados a dar un hexágono regular, luego doblar repetidamente el número de lados a medida que el área del polígono se acercaba más y más a la del círculo (e hizo lo mismo con los polígonos circunscritos).

El científico suizo Johann Heinrich Lambert en 1761 demostró que π, la relación entre el área de un círculo y su radio al cuadrado, es irracional, lo que significa que no es igual al cociente de dos números enteros. En 1794 el matemático francés Adrien-Marie Legendre demostró que π es irracional; esto también prueba que π es irracional. En 1882, el matemático alemán Ferdinand von Lindemann demostró que π es trascendental (no la solución de ninguna ecuación polinómica con coeficientes racionales), lo que confirma una conjetura hecha por Legendre y Euler.

Área del triángulo

Garza (o Héroe) de Alejandría encontró lo que se conoce como la fórmula de Herón para el área de un triángulo en términos de sus lados, y una prueba se puede encontrar en su libro, Metrica , escrito alrededor del año 60 EC. Se ha sugerido que Arquímedes conocía la fórmula dos siglos antes, y dado que Metrica es una colección del conocimiento matemático disponible en el mundo antiguo, es posible que la fórmula sea anterior a la referencia dada en ese trabajo.

En 499, Aryabhata, un gran astrónomo matemático de la era clásica de las matemáticas indias y la astronomía india, expresó el área de un triángulo como la mitad de la base multiplicada por la altura en el Aryabhatiya (sección 2.6).

Los chinos descubrieron una fórmula equivalente a la de Heron independientemente de los griegos. Fue publicado en 1247 en Shushu Jiuzhang ("Tratado matemático en nueve secciones"), escrito por Qin Jiushao.

Área cuadrilátera

En el siglo VII EC, Brahmagupta desarrolló una fórmula, ahora conocida como la fórmula de Brahmagupta, para el área de un cuadrilátero cíclico (un cuadrilátero inscrito en un círculo) en términos de sus lados. En 1842, los matemáticos alemanes Carl Anton Bretschneider y Karl Georg Christian von Staudt encontraron de manera independiente una fórmula, conocida como fórmula de Bretschneider, para el área de cualquier cuadrilátero.

Área general del polígono

El desarrollo de coordenadas cartesianas por René Descartes en el siglo XVII permitió el desarrollo de la fórmula del topógrafo para el área de cualquier polígono con ubicaciones de vértices conocidas por Gauss en el siglo XIX.

Áreas determinadas usando cálculo

El desarrollo del cálculo integral a fines del siglo XVII proporcionó herramientas que posteriormente podrían utilizarse para calcular áreas más complicadas, como el área de una elipse y las superficies de varios objetos tridimensionales curvos.

Fórmulas de área

Fórmulas poligonales

Para un polígono que no se interseca a sí mismo (simple), las coordenadas cartesianas ( i = 0, 1, ..., n -1) de cuyos n vértices se conocen, el área está dada por la fórmula del agrimensor:

(x_ {i}, y_ {i})

A = {\ frac {1} {2}} | \ sum _ {{i = 0}} ^ {{n-1}} (x_ {i} y _ {{i + 1}} - x _ {{i + 1}} y_ {i}) |

donde cuando i = n -1, entonces i +1 se expresa como módulo ny entonces se refiere a 0.

Rectángulos

Un rectángulo con longitud y ancho etiquetados

El área de este rectángulo es

lw

.

La fórmula de área más básica es la fórmula para el área de un rectángulo. Dado un rectángulo con longitud

l

y ancho

w

, la fórmula para el área es:

A = lw

(rectángulo).

Es decir, el área del rectángulo es la longitud multiplicada por el ancho. Como un caso especial, como

l = w

en el caso de un cuadrado, el área de un cuadrado con una longitud lateral

s

viene dada por la fórmula:

A = s

(cuadrado).

La fórmula para el área de un rectángulo se sigue directamente de las propiedades básicas del área, y a veces se toma como una definición o axioma. Por otro lado, si la geometría se desarrolla antes de la aritmética, esta fórmula se puede usar para definir la multiplicación de números reales.

Un diagrama que muestra cómo se puede reorganizar un paralelogramo en la forma de un rectángulo

Iguales cifras de área.

Disección, paralelogramos y triángulos

La mayoría de las otras fórmulas simples para el área se siguen del método de disección. Esto implica cortar una forma en pedazos, cuyas áreas deben sumar al área de la forma original.

Por ejemplo, cualquier paralelogramo se puede subdividir en un trapecio y un triángulo rectángulo, como se muestra en la figura a la izquierda. Si el triángulo se mueve al otro lado del trapecio, la figura resultante es un rectángulo. Se deduce que el área del paralelogramo es la misma que el área del rectángulo:

A = bh

(paralelogramo).

Dos triángulos iguales.

Sin embargo, el mismo paralelogramo también se puede cortar a lo largo de una diagonal en dos triángulos congruentes, como se muestra en la figura a la derecha. Se deduce que el área de cada triángulo es la mitad del área del paralelogramo:

A = {\ frac {1} {2}} bh

(triángulo).

Se pueden usar argumentos similares para encontrar fórmulas de área para el trapecio así como polígonos más complicados.

Área de formas curvas

Círculos

Un círculo dividido en muchos sectores se puede reorganizar aproximadamente para formar un paralelogramo

Un círculo se puede dividir en sectores que se reorganizan para formar un paralelogramo aproximado.

La fórmula para el área de un círculo (más propiamente llamada el área encerrada por un círculo o el área de un disco) se basa en un método similar. Dado un círculo de radio

r

, es posible dividir el círculo en sectores, como se muestra en la figura de la derecha. Cada sector tiene una forma aproximadamente triangular, y los sectores se pueden reorganizar para formar un paralelogramo aproximado. La altura de este paralelogramo es

r

, y el ancho es la mitad de la circunferencia del círculo, o

π r

. Por lo tanto, el área total del círculo es

π r

:

A = π r

(círculo).

Aunque la disección utilizada en esta fórmula es solo aproximada, el error se reduce a medida que el círculo se divide en más y más sectores. El límite de las áreas de los paralelogramos aproximados es exactamente

π r

, que es el área del círculo.

Este argumento es en realidad una aplicación simple de las ideas de cálculo. En la antigüedad, el método del agotamiento se usaba de manera similar para encontrar el área del círculo, y este método ahora se reconoce como un precursor del cálculo integral. Usando métodos modernos, el área de un círculo se puede calcular usando una integral definida:

{\ displaystyle A \; = \; 2 \ int _ {- r} ^ {r} {\ sqrt {r ^ {2} -x ^ {2}}} \, dx \; = \; \ pi r ^ {2}.}

Elipses

La fórmula para el área encerrada por una elipse se relaciona con la fórmula de un círculo; para una elipse con semi-mayor y semi-menores ejes

x

y

y

la fórmula es:

{\ displaystyle A = \ pi xy.}

Área de superficie

Arquímedes demostró que el área de superficie de una esfera es exactamente cuatro veces el área de un disco plano del mismo radio, y el volumen encerrado por la esfera es exactamente 2/3 del volumen de un cilindro de la misma altura y radio.

La mayoría de las fórmulas básicas para el área de superficie pueden obtenerse cortando superficies y aplanándolas. Por ejemplo, si la superficie lateral de un cilindro (o cualquier prisma) se corta longitudinalmente, la superficie se puede aplanar en un rectángulo. De manera similar, si se realiza un corte a lo largo del costado de un cono, la superficie lateral puede aplanarse en un sector de un círculo y calcularse el área resultante.

La fórmula para el área de superficie de una esfera es más difícil de derivar: como una esfera tiene una curvatura gaussiana distinta de cero, no se puede aplanar. La fórmula para el área de superficie de una esfera fue obtenida por primera vez por Arquímedes en su obra Sobre la esfera y el cilindro . La fórmula es:

A = 4 πr

(esfera),

donde

r

es el radio de la esfera. Al igual que con la fórmula para el área de un círculo, cualquier derivación de esta fórmula inherentemente utiliza métodos similares al cálculo.

Fórmulas generales

Áreas de figuras bidimensionales

Un triángulo: (donde B es cualquier lado, y h es la distancia desde la línea en la que B se encuentra al otro vértice del triángulo). Esta fórmula se puede usar si se conoce la altura h . Si se conocen las longitudes de los tres lados, se puede usar la fórmula de Heron : donde a, b , c son los lados del triángulo, y es la mitad de su perímetro. Si se da un ángulo y sus dos lados incluidos, el área es donde $C$ es el ángulo dado y $a$ y $b$ ${\ tfrac 12} Bh$ ${\ sqrt {s (sa) (sb) (sc)}}$ $s = {\ tfrac 12} (a + b + c)$ ${\ tfrac 12} ab \ sin (C)$ son sus lados incluidos. Si el triángulo se representa gráficamente en un plano de coordenadas, se puede usar una matriz y se simplifica al valor absoluto de . Esta fórmula también se conoce como la fórmula del cordón y es una forma fácil de resolver para el área de un triángulo de coordenadas al sustituir los 3 puntos (x 1 , y 1 ) , (x 2 , y 2 ) y (x 3 , y 3 ) . La fórmula del cordón también se puede usar para encontrar las áreas de otros polígonos cuando se conocen sus vértices. Otro enfoque para un triángulo de coordenadas es usar cálculo para encontrar el área. ${\ tfrac 12} (x_ {1} y_ {2} + x_ {2} y_ {3} + x_ {3} y_ {1} -x_ {2} y_ {1} -x_ {3} y_ {2} -x_ {1} y_ {3})$
Un polígono simple construido en una cuadrícula de puntos equidistantes (es decir, puntos con coordenadas enteras) tales que todos los vértices del polígono son puntos de cuadrícula:, donde i es el número de puntos de cuadrícula dentro del polígono yb es el número de puntos límite . Este resultado se conoce como el teorema de Pick. $i + {\ frac {b} {2}} - 1$

Área en cálculo

La integración puede considerarse como la medición del área bajo una curva, definida por f ( x ), entre dos puntos (aquí a y b ).

Un diagrama que muestra el área entre dos funciones

El área entre dos gráficos se puede evaluar calculando la diferencia entre las integrales de las dos funciones

El área entre una curva de valor positivo y el eje horizontal, medida entre dos valores de un y b (b se define como el mayor de los dos valores) en el eje horizontal, está dada por la integral de una a b de la función que representa la curva:

{\ displaystyle A = \ int _ {a} ^ {b} f (x) \, dx.}

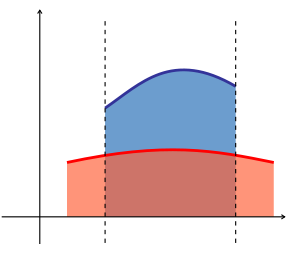
El área entre los gráficos de dos funciones es igual a la integral de una función, f ( x ), menos la integral de la otra función, g ( x ):

{\ displaystyle A = \ int _ {a} ^ {b} (f (x) -g (x)) \, dx,}

¿Dónde está la curva con el mayor valor de y?

f (x)

Un área delimitada por una función r = r (θ) expresada en coordenadas polares es:

{\ displaystyle A = {1 \ over 2} \ int r ^ {2} \, d \ theta.}

El área delimitada por una curva paramétrica con puntos finales viene dada por las integrales de línea: ${\ vec u} (t) = (x (t), y (t))$ ${\ vec u} (t_ {0}) = {\ vec u} (t_ {1})$

\ oint _ {{t_ {0}}} ^ {{t_ {1}}} x {\ dot y} \, dt = - \ oint _ {{t_ {0}}} ^ {{t_ {1}} } y {\ dot x} \, dt = {1 \ over 2} \ oint _ {{t_ {0}}} ^ {{t_ {1}}} (x {\ dot y} -y {\ dot x }) \, dt

(ver el teorema de Green) o el componente z de

{1 \ over 2} \ oint _ {{t_ {0}}} ^ {{t_ {1}}} {\ vec u} \ times {\ dot {{\ vec u}}} \, dt.

Área delimitada entre dos funciones cuadráticas

Para encontrar el área delimitada entre dos funciones cuadráticas, restamos una de la otra para escribir la diferencia como

{\ displaystyle f (x) -g (x) = ax ^ {2} + bx + c = a (x- \ alpha) (x- \ beta)}

donde f ( x ) es el límite superior cuadrático y g ( x ) es el límite inferior cuadrático. Defina el discriminante de f ( x ) - g ( x ) como

\ Delta = b ^ {2} -4ac.

Al simplificar la fórmula integral entre los gráficos de dos funciones (como se da en la sección anterior) y al usar la fórmula de Vieta, podemos obtener

{\ displaystyle A = {\ frac {\ Delta {\ sqrt {\ Delta}}} {6a ^ {2}}} = {\ frac {a} {6}} (\ beta - \ alpha) ^ {3} , \ qquad a \ neq 0.}

Lo anterior sigue siendo válido si una de las funciones de límite es lineal en lugar de cuadrática.

Área de superficie de figuras tridimensionales

Cono:, donde r es el radio de la base circular, y h es la altura. Eso también puede reescribirse como o donde r es el radio yl es la altura inclinada del cono. es el área de la base mientras que es el área de la superficie lateral del cono. $\ pi r \ left (r + {\ sqrt {r ^ {2} + h ^ {2}}} \ right)$ $\ pi r ^ {2} + \ pi rl$ $\ pi r (r + l) \, \!$ $\ pi r ^ {2}$ $\ pi rl$
cubo:, donde s es la longitud de un borde. $6s ^ 2$
cilindro:, donde r es el radio de una base y h es la altura. El 2 r también se puede reescribir como d , donde d es el diámetro. $2 \ pi r (r + h)$ $\Pi$ $\Pi$
prisma: 2B + Ph, donde B es el área de una base, P es el perímetro de una base y h es la altura del prisma.
pirámide:, donde B es el área de la base, P es el perímetro de la base y L es la longitud de la inclinación. $B + \ frac {PL} {2}$
prisma rectangular:, donde es la longitud, w es el ancho, y h es la altura. $2 (\ ell w + \ ell h + wh)$ $\ana$

Fórmula general para el área de superficie

La fórmula general para el área de superficie del gráfico de una función continuamente diferenciable donde y es una región en el plano xy con el límite suave:

z = f (x, y),

(x, y) \ en D \ subconjunto {\ mathbb {R}} ^ {2}

re

A = \ iint _ {D} {\ sqrt {\ left ({\ frac {\ partial f} {\ partial x}} \ right) ^ {2} + \ left ({\ frac {\ partial f} {\ partial y}} \ right) ^ {2} +1}} \, dx \, dy.

Una fórmula aún más general para el área de la gráfica de una superficie paramétrica en la forma vectorial donde es una función de vector continuamente diferenciable es:

{\ mathbf {r}} = {\ mathbf {r}} (u, v),

\ mathbf {r}

(u, v) \ en D \ subconjunto {\ mathbb {R}} ^ {2}

A = \ iint _ {D} \ left | {\ frac {\ partial {\ mathbf {r}}} {\ partial u}} \ times {\ frac {\ partial {\ mathbf {r}}} {\ partial v}} \ right | \, du \, dv.

Lista de fórmulas

Fórmulas comunes adicionales para el área:
Forma	Fórmula	Variables
Triángulo regular (triángulo equilátero)	${\ frac {{\ sqrt {3}}} {4}} s ^ {2} \, \!$	$s$ es la longitud de un lado del triángulo.
Triángulo	${\ sqrt {s (sa) (sb) (sc)}} \, \!$	$s$ es la mitad del perímetro, , y son la longitud de cada lado. $un$ $segundo$ $do$
Triángulo	${\ tfrac 12} ab \ sin (C) \, \!$	$un$ y son dos lados, y es el ángulo entre ellos. $segundo$ $do$
Triángulo	${\ tfrac 12} bh \, \!$	$segundo$ y son la base y la altitud (medidas perpendiculares a la base), respectivamente. $h$
Triángulo isósceles	${\ frac {1} {2}} b {\ sqrt {a ^ {2} - {\ frac {b ^ {2}} {4}}}} = {\ frac {b} {4}} {\ sqrt {4a ^ {2} -b ^ {2}}}$	$un$ es la longitud de uno de los dos lados iguales y es la longitud de un lado diferente. $segundo$
Rombo / cometa	${\ tfrac {1} {2}} ab$	$un$ y son las longitudes de las dos diagonales del rombo o cometa. $segundo$
Paralelogramo	$bh \, \!$	$segundo$ es la longitud de la base y es la altura perpendicular. $h$
Trapecio	${\ frac {(a + b) h} {2}} \, \!$	$un$ y son los lados paralelos y la distancia (altura) entre los paralelos. $segundo$ $h$
Hexágono regular	${\ frac {3} {2}} {\ sqrt {3}} s ^ {2} \, \!$	$s$ es la longitud de un lado del hexágono.
Octágono regular	$2 (1 + {\ sqrt {2}}) s ^ {2} \, \!$	$s$ es la longitud de un lado del octágono.
Polígono regular	${\ frac {1} {4}} nl ^ {2} \ cdot \ cot (\ pi / n) \, \!$	$l$ es la longitud del lado y es el número de lados. $norte$
Polígono regular	${\ frac {1} {4n}} p ^ {2} \ cdot \ cot (\ pi / n) \, \!$	$pag$ es el perímetro y es el número de lados. $norte$
Polígono regular	${\ frac {1} {2}} nR ^ {2} \ cdot \ sin (2 \ pi / n) = nr ^ {2} \ tan (\ pi / n) \, \!$	$R$ es el radio de un círculo circunscrito, es el radio de un círculo inscrito, y es el número de lados. $r$ $norte$
Polígono regular	${\ tfrac 12} ap = {\ tfrac 12} nsa \, \!$	$norte$ es el número de lados, es la longitud del lado, es la apotema, o el radio de un círculo inscrito en el polígono, y es el perímetro del polígono. $s$ $un$ $pag$
Circulo	$\ pi r ^ {2} \ {\ text {o}} \ {\ frac {\ pi d ^ {2}} {4}} \, \!$	$r$ es el radio y el diámetro. $re$
Sector circular	${\ frac {\ theta} {2}} r ^ {2} \ {\ text {o}} \ {\ frac {L \ cdot r} {2}} \, \!$	$r$ y son el radio y el ángulo (en radianes), respectivamente, y es la longitud del perímetro. $\ theta$ $L$
Elipse	$\ pi ab \, \!$	$un$ y son los ejes semi-mayor y semi-menor, respectivamente. $segundo$
Superficie total de un cilindro	$2 \ pi r (r + h) \, \!$	$r$ y son el radio y la altura, respectivamente. $h$
Área de superficie lateral de un cilindro	$2 \ pi rh \, \!$	$r$ y son el radio y la altura, respectivamente. $h$
Superficie total de una esfera	$4 \ pi r ^ {2} \ {\ text {o}} \ \ pi d ^ {2} \, \!$	$r$ y son el radio y el diámetro, respectivamente. $re$
Superficie total de una pirámide	$B + {\ frac {PL} {2}} \, \!$	$segundo$ es el área de la base, es el perímetro de la base y es la altura inclinada. $PAG$ $L$
Superficie total de un pyramidfrustum	$B + {\ frac {PL} {2}} \, \!$	$segundo$ es el área de la base, es el perímetro de la base y es la altura inclinada. $PAG$ $L$
Conversión de área cuadrada a circular	${\ frac {4} {\ pi}} A \, \!$	$UN$ es el área del cuadrado en unidades cuadradas.
Conversión circular a área cuadrada	${\ frac {\ pi} {4}} C \, \!$	$do$ es el área del círculo en unidades circulares.

Los cálculos anteriores muestran cómo encontrar las áreas de muchas formas comunes.

Las áreas de polígonos irregulares se pueden calcular utilizando la "fórmula del topógrafo".

Relación del área con el perímetro

La desigualdad isoperimétrica indica que, para una curva cerrada de longitud L (por lo que la región que delimita tiene un perímetro L ) y para el área A de la región que abarca,

4 \ pi A \ leq L ^ {2},

y la igualdad se cumple si y solo si la curva es un círculo. Por lo tanto, un círculo tiene el área más grande de cualquier figura cerrada con un perímetro dado.

En el otro extremo, una figura con un perímetro L dado podría tener un área arbitrariamente pequeña, como lo ilustra un rombo que está "inclinado" arbitrariamente lejos de modo que dos de sus ángulos están arbitrariamente cerca de 0 ° y los otros dos están arbitrariamente cerca a 180 °.

Para un círculo, la relación entre el área y la circunferencia (el término para el perímetro de un círculo) es igual a la mitad del radio r . Esto puede verse a partir de la fórmula de área πr y la fórmula de circunferencia 2 πr .

El área de un polígono regular es la mitad de su perímetro por la apotema (donde la apotema es la distancia desde el centro hasta el punto más cercano en cualquier lado).

Fractales

Duplicar las longitudes de los bordes de un polígono multiplica su área por cuatro, que es dos (la relación entre la longitud del lado nuevo y el viejo) elevada a la potencia de dos (la dimensión del espacio en el que reside el polígono). Pero si se duplican las longitudes unidimensionales de un fractal dibujado en dos dimensiones, el contenido espacial del fractal se escala por una potencia de dos que no es necesariamente un número entero. Este poder se llama dimensión fractal del fractal.

Bisectrices de área

Hay una infinitud de líneas que bisecan el área de un triángulo. Tres de ellos son las medianas del triángulo (que conectan los puntos medios de los lados con los vértices opuestos), y estos son concurrentes en el centroide del triángulo; de hecho, son las únicas bisectrices de área que pasan por el centroide. Cualquier línea a través de un triángulo que divide el área del triángulo y su perímetro por la mitad pasa por el incentro del triángulo (el centro de su círculo). Hay uno, dos o tres de estos para cualquier triángulo dado.

Cualquier línea a través del punto medio de un paralelogramo divide el área en dos.

Todas las bisectrices de área de un círculo u otra elipse pasan por el centro, y cualquier acorde a través del centro biseca el área. En el caso de un círculo, son los diámetros del círculo.

Mejoramiento

Dado un contorno de alambre, la superficie de menor área que abarca ("relleno") es una superficie mínima. Ejemplos familiares incluyen pompas de jabón.

La cuestión del área de llenado del círculo riemanniano permanece abierta.

El círculo tiene el área más grande de cualquier objeto bidimensional que tenga el mismo perímetro.

Un polígono cíclico (uno inscrito en un círculo) tiene el área más grande de cualquier polígono con un número dado de lados de la misma longitud.

Una versión de la desigualdad isoperimétrica para triángulos establece que el triángulo de mayor área entre todos aquellos con un perímetro dado es equilátero.

El triángulo del área más grande de todos los inscritos en un círculo dado es equilátero; y el triángulo de área más pequeña de todas las circunscritas alrededor de un círculo dado es equilátero.

La relación entre el área del incircle y el área de un triángulo equilátero es más grande que la de cualquier triángulo no equilátero.

{\ frac {\ pi} {3 {\ sqrt {3}}}}

La relación entre el área y el cuadrado del perímetro de un triángulo equilátero es mayor que la de cualquier otro triángulo.

\ frac {1} {12 \ sqrt {3}},

Buscar en este blog