Algoritmo
Definición
En matemáticas y ciencias de la computación, un algoritmo ( / æ l del ɡ del ə r ɪ ð əm / (  escuchar ) ) es una especificación inequívoca de cómo resolver una clase de problemas. Los algoritmos pueden realizar tareas de cálculo, procesamiento de datos y razonamiento automático.
escuchar ) ) es una especificación inequívoca de cómo resolver una clase de problemas. Los algoritmos pueden realizar tareas de cálculo, procesamiento de datos y razonamiento automático.
Como método eficaz, un algoritmo se puede expresar dentro de una cantidad finita de espacio y tiempo y en un lenguaje formal bien definido para calcular una función. Comenzando por un estado inicial y una entrada inicial (quizás vacía), las instrucciones describen un cálculo que, cuando se ejecuta, avanza a través de un número finito de estados sucesivos bien definidos, produciendo eventualmente "salida" y terminando en un estado final final. La transición de un estado a otro no es necesariamente determinista; algunos algoritmos, conocidos como algoritmos aleatorios, incorporan entrada aleatoria.
El concepto de algoritmo ha existido durante siglos y el uso del concepto puede atribuirse a los matemáticos griegos, por ejemplo, el tamiz de Eratóstenes y el algoritmo de Euclides; el término algoritmo en sí se deriva del matemático del siglo IX Muḥammad ibn Mūsā al'Khwārizmī, latinizado 'Algoritmi'. Una formalización parcial de lo que se convertiría en la noción moderna de algoritmo comenzó con los intentos de resolver el Entscheidungsproblem (el "problema de decisión") planteado por David Hilbert en 1928. Las formalizaciones posteriores se enmarcaron como intentos de definir "calculabilidad efectiva" o "método efectivo"; esas formalizaciones incluyeron las funciones recursivas de Gödel-Herbrand-Kleene de 1930, 1934 y 1935, el cálculo lambda de la Iglesia Alonzo de 1936, la Formulación 1 de 1936 de Emil Post y las máquinas de Turing de Alan Turing de 1936-7 y 1939.
Etimología
La palabra "algoritmo" tiene sus raíces en latinizar el nombre de Muhammad ibn Musa al-Khwarizmi en un primer paso hacia el algoritmo . Al-Khwārizmī (persa: خوارزمی , hacia 780-850) fue un matemático persa, astrónomo, geógrafo y erudito de la Casa de la Sabiduría en Bagdad, cuyo nombre significa "el nativo de Khwarezm", una región que formó parte de la Gran Irán y ahora está en Uzbekistán.
Alrededor de 825, al-Khwarizmi escribió un tratado en árabe sobre el sistema numérico hindú-árabe, que fue traducido al latín en el siglo XII bajo el título Algoritmi de numero Indorum . Este título significa "Algoritmi en los números de los indios", donde "Algoritmi" era la latinización del traductor del nombre de Al-Khwarizmi. Al-Khwarizmi fue el matemático más leído en Europa a finales de la Edad Media, principalmente a través de otro de sus libros, el Álgebra. En latín medieval tardío, algorismus , 'algorismo' inglés, la corrupción de su nombre, simplemente significaba el "sistema decimal de números". En el siglo XV, bajo la influencia de la palabra griega ἀριθμός 'número' ( cf. 'aritmética'), , y el término inglés correspondiente "algoritmo" se atestigua por primera vez en el siglo XVII; el sentido moderno fue introducido en el siglo XIX.
En inglés, fue utilizado por primera vez alrededor de 1230 y luego por Chaucer en 1391. El inglés adoptó el término francés, pero no fue hasta finales del siglo XIX que el "algoritmo" adquirió el significado que tiene en el inglés moderno.
Otro uso temprano de la palabra es desde 1240, en un manual titulado Carmen de Algorismo compuesto por Alexandre de Villedieu. Comienza así:
que se traduce como:
El poema tiene unos pocos cientos de líneas y resume el arte de calcular con el nuevo estilo de dados indios, o Talibus Indorum, o números hindúes.
Definición informal
Una definición informal podría ser "un conjunto de reglas que define con precisión una secuencia de operaciones". que incluiría todos los programas de computadora, incluidos los programas que no realizan cálculos numéricos. En general, un programa es solo un algoritmo si finalmente se detiene.
Un ejemplo prototípico de un algoritmo es el algoritmo euclidiano para determinar el divisor común máximo de dos enteros; un ejemplo (hay otros) es descrito por el flowchartabove y como un ejemplo en una sección posterior.
Boolos, Jeffrey y 1974, 1999 ofrecen un significado informal de la palabra en la siguiente cita:
Un "conjunto enumerablemente infinito" es aquel cuyos elementos se pueden poner en correspondencia uno a uno con los enteros. Por lo tanto, Boolos y Jeffrey están diciendo que un algoritmo implica instrucciones para un proceso que "crea" números enteros de salida a partir de un entero arbitrario de "entrada" o enteros que, en teoría, pueden ser arbitrariamente grandes. Así, un algoritmo puede ser una ecuación algebraica tal como = y m + n - dos "variables de entrada" arbitrarias m y n que producen una salida y . Pero los intentos de varios autores para definir la noción indican que la palabra implica mucho más que esto, algo del orden de (para el ejemplo de adición):
- Instrucciones precisas (en el lenguaje entendido por "la computadora") para un proceso rápido, eficiente y "bueno" que especifica los "movimientos" de "la computadora" (máquina o ser humano, equipado con la información y capacidades internas contenidas necesarias) para encontrar , decodificar, y después del proceso de entrada arbitraria enteros / símbolos m y n , símbolos + y = ... y "eficacia" producir, en un tiempo "razonable", la salida de enteros y en un lugar determinado y en un formato especificado.
El concepto de algoritmo también se utiliza para definir la noción de decidability. Esa noción es central para explicar cómo se forman los sistemas formales a partir de un pequeño conjunto de axiomas y reglas. En lógica, el tiempo que un algoritmo requiere completar no se puede medir, ya que aparentemente no está relacionado con nuestra dimensión física habitual. A partir de tales incertidumbres, que caracterizan el trabajo en curso, surge la falta de disponibilidad de una definición de algoritmo que se adapte tanto al uso concreto (en cierto sentido) como abstracto del término.
Formalización
Los algoritmos son esenciales para la forma en que las computadoras procesan los datos. Muchos programas de computadora contienen algoritmos que detallan las instrucciones específicas que una computadora debe realizar (en un orden específico) para llevar a cabo una tarea específica, como calcular los cheques de pago de los empleados o imprimir boletas de calificaciones de los estudiantes. Por lo tanto, se puede considerar que un algoritmo es cualquier secuencia de operaciones que pueda ser simulada por un sistema Turing-complete. Los autores que afirman esta tesis incluyen Minsky (1967), Savage (1987) y Gurevich (2000):
Típicamente, cuando un algoritmo está asociado con la información de procesamiento, los datos pueden leerse desde una fuente de entrada, escribirse en un dispositivo de salida y almacenarse para un procesamiento posterior. Los datos almacenados se consideran parte del estado interno de la entidad que realiza el algoritmo. En la práctica, el estado se almacena en una o más estructuras de datos.
Para algunos de estos procesos computacionales, el algoritmo debe estar rigurosamente definido: especificado en la forma en que se aplica en todas las circunstancias posibles que puedan surgir. Es decir, cualquier paso condicional debe tratarse sistemáticamente, caso por caso; los criterios para cada caso deben ser claros (y computables).
Debido a que un algoritmo es una lista precisa de pasos precisos, el orden del cálculo siempre es crucial para el funcionamiento del algoritmo. Generalmente, se supone que las instrucciones se enumeran explícitamente, y se describen como comenzando "desde arriba" y yendo "hacia abajo", una idea que se describe más formalmente por flujo de control .
Hasta ahora, esta discusión sobre la formalización de un algoritmo ha asumido las premisas de la programación imperativa. Esta es la concepción más común e intenta describir una tarea en medios discretos y "mecánicos". Único en esta concepción de algoritmos formalizados es la operación de asignación, que establece el valor de una variable. Se deriva de la intuición de "memoria" como un bloc de notas. Hay un ejemplo debajo de tal asignación.
Para algunas concepciones alternativas de lo que constituye un algoritmo, ver programación funcional y programación lógica.
Expresando algoritmos
Los algoritmos se pueden expresar en muchos tipos de notación, incluidos los lenguajes naturales, pseudocódigo, diagramas de flujo, diagramas de drakón, lenguajes de programación o tablas de control (procesados por intérpretes). Las expresiones de algoritmos en lenguaje natural tienden a ser detalladas y ambiguas, y rara vez se usan para algoritmos complejos o técnicos. El pseudocódigo, los diagramas de flujo, las tablas de control y las tablas de control son formas estructuradas de expresar algoritmos que evitan muchas de las ambigüedades comunes en las declaraciones de lenguaje natural. Los lenguajes de programación están destinados principalmente a expresar algoritmos en una forma que pueda ser ejecutada por una computadora, pero a menudo se usan como una forma de definir o documentar algoritmos.
Existe una amplia variedad de representaciones posibles y se puede expresar un programa de máquina de Turing dado como una secuencia de tablas de máquina (ver más en máquina de estado finito, tabla de transición de estado y tabla de control), como diagramas de flujo y gráficos de drakon (ver más en el estado diagrama), o como una forma de código de máquina rudimentario o código de conjunto llamado "conjuntos de cuádruples" (ver más en la máquina de Turing).
Las representaciones de los algoritmos se pueden clasificar en tres niveles aceptados de la descripción de la máquina de Turing:
- 1 Descripción de alto nivel
- "... en prosa para describir un algoritmo, ignorando los detalles de implementación. En este nivel no es necesario mencionar cómo la máquina gestiona su cinta o cabezal".
- 2 Descripción de la implementación
- "... prosa utilizada para definir la forma en que la máquina de Turing utiliza su cabeza y la forma en que almacena datos en su cinta. En este nivel no damos detalles de los estados o la función de transición".
- 3 Descripción formal
- El más detallado, el "nivel más bajo", da la "tabla de estados" de la máquina Turing.
Para ver un ejemplo del algoritmo simple "Agregar m + n" descrito en los tres niveles, vea Algoritmo # Ejemplos.
Diseño
El diseño del algoritmo se refiere a un método o proceso matemático para resolver problemas y algoritmos de ingeniería. El diseño de algoritmos es parte de muchas teorías de solución de investigación operativa, como programación dinámica y divide y vencerás. Las técnicas para diseñar e implementar diseños de algoritmo también se denominan patrones de diseño de algoritmo, como el patrón de método de plantilla y el patrón de decorador.
Uno de los aspectos más importantes del diseño de algoritmos es crear un algoritmo que tenga un tiempo de ejecución eficiente, también conocido como Big O.
Pasos típicos en el desarrollo de algoritmos:
- Definición del problema
- Desarrollo de un modelo
- Especificación de algoritmo
- Diseñando un algoritmo
- Comprobando la corrección del algoritmo
- Análisis de algoritmo
- Implementación de algoritmo
- Prueba de programa
- Preparación de documentación
Implementación
La mayoría de los algoritmos están destinados a ser implementados como programas de computadora. Sin embargo, los algoritmos también se implementan por otros medios, como en una red neuronal biológica (por ejemplo, el cerebro humano que implementa la aritmética o un insecto que busca alimento), en un circuito eléctrico o en un dispositivo mecánico.
Algoritmos de computadora
En sistemas informáticos, un algoritmo es básicamente una instancia de lógica escrito en software por los desarrolladores de software para ser eficaz para el equipo destinado "objetivo" (s) para producir salida de dado (tal vez null) de entrada . Un algoritmo óptimo, incluso funcionando en hardware antiguo, produciría resultados más rápidos que un algoritmo no óptimo (complejidad de tiempo más alta) para el mismo propósito, ejecutándose en un hardware más eficiente; es por eso que los algoritmos, como el hardware de la computadora, se consideran tecnología.
Programas "elegantes" (compactos), programas "buenos" (rápidos) : la noción de "simplicidad y elegancia" aparece informalmente en Knuth y precisamente en Chaitin:
- Knuth: "... queremos buenos algoritmos en algún sentido estético vagamente definido. Un criterio ... es el tiempo que lleva realizar el algoritmo ... Otros criterios son la adaptabilidad del algoritmo a las computadoras, su simplicidad y elegancia. , etc.
- Chaitin: "... un programa es 'elegante', con lo que quiero decir que es el programa más pequeño posible para producir el resultado que lo hace"
Chaitin introduce su definición con anterioridad: "Mostraré que no puede probar que un programa es 'elegante'"; una prueba de este tipo resolvería el problema de la detención (ibid).
Algoritmo versus función computable por un algoritmo : para una función determinada, pueden existir múltiples algoritmos. Esto es cierto, incluso sin expandir el conjunto de instrucciones disponibles disponibles para el programador. Rogers observa que "es ... importante distinguir entre la noción de algoritmo , es decir, el procedimiento y la noción de función computable por algoritmo , es decir, mapeo cedido por procedimiento. La misma función puede tener varios algoritmos diferentes".
Desafortunadamente, puede haber una compensación entre bondad (velocidad) y elegancia (compacidad): un programa elegante puede tomar más pasos para completar un cálculo que uno menos elegante. Un ejemplo que usa el algoritmo de Euclides aparece a continuación.
Computadoras (y computors), modelos de computación : una computadora (o "computor" humano) es un tipo restringido de máquina, un "dispositivo mecánico determinista discreto" que sigue ciegamente sus instrucciones. Los modelos primitivos de Melzak y Lambek redujeron esta noción a cuatro elementos: (i) ubicaciones discretas y distinguibles , (ii) contadores discretos e indistinguibles (iii) un agente, y (iv) una lista de instrucciones que son efectivas con relación a la capacidad del agente.
Minsky describe una variación más agradable del modelo de "ábaco" de Lambek en sus "Bases muy simples para computabilidad". La máquina de Minsky avanza secuencialmente a través de sus cinco (o seis, dependiendo de cómo cuente) las instrucciones, a menos que un IF-THEN GOTO condicional o un programa de cambios GOTO incondicional salgan de la secuencia. Además de HALT, la máquina de Minsky incluye tres operaciones de asignación (sustitución, sustitución): CERO (por ejemplo, el contenido de la ubicación reemplazado por 0: L ← 0), SUCESOR (por ejemplo, L ← L + 1) y DECRETO (por ejemplo, L ← L - 1 ) Rara vez debe un programador escribir "código" con un conjunto de instrucciones tan limitado. Pero Minsky muestra (al igual que Melzak y Lambek) que su máquina está completa con solo cuatro tipos generales de Turing de instrucciones: GOTO condicional, GOTO incondicional, asignación / sustitución / sustitución y HALT.
Simulación de un algoritmo: lenguaje de computadora (computor) : Knuth aconseja al lector que "la mejor manera de aprender un algoritmo es probarlo ... inmediatamente tome papel y lápiz y trabaje con un ejemplo". Pero, ¿qué tal una simulación o ejecución de lo real? El programador debe traducir el algoritmo a un lenguaje que el simulador / computadora / computor pueda ejecutar efectivamente . Stone da un ejemplo de esto: al calcular las raíces de una ecuación cuadrática, el computor debe saber cómo tomar una raíz cuadrada. Si no lo hacen, entonces el algoritmo, para ser efectivo, debe proporcionar un conjunto de reglas para extraer una raíz cuadrada.
Esto significa que el programador debe conocer un "lenguaje" que sea efectivo en relación con el agente informático de destino (computadora / computor).
Pero, ¿qué modelo debería usarse para la simulación? Van Emde Boas observa que "incluso si basamos la teoría de la complejidad en máquinas abstractas en lugar de concretas, permanece la arbitrariedad de la elección de un modelo. Es en este punto donde entra la noción de simulación ". Cuando se mide la velocidad, el conjunto de instrucciones es importante. Por ejemplo, el subprograma en el algoritmo de Euclides para calcular el resto se ejecutaría mucho más rápido si el programador tuviera una instrucción de "módulo" disponible en lugar de simplemente resta (o peor: solo el "decremento" de Minsky).
Programación estructurada, estructuras canónicas: Según la tesis Church-Turing, cualquier algoritmo puede calcularse mediante un modelo conocido como Turing completo, y según las demostraciones de Minsky, la integridad de Turing requiere solo cuatro tipos de instrucción: GOTO condicional, GOTO incondicional, asignación, HALT. Kemeny y Kurtz observan que, si bien el uso "indisciplinado" de GOTOs incondicionales y GOTOs IF-THEN condicionales puede dar como resultado un "código de spaghetti", un programador puede escribir programas estructurados usando solo estas instrucciones; por otro lado, "también es posible, y no demasiado difícil, escribir programas mal estructurados en un lenguaje estructurado". Tausworthe aumenta las tres estructuras canónicas de Böhm-Jacopini: SEQUENCE, IF-THEN-ELSE y WHILE-DO, con dos más: DO-WHILE y CASE.
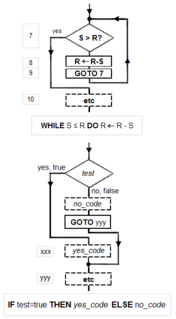
Símbolos de diagramas de flujo canónicos : el asistente gráfico llamado diagrama de flujo ofrece una forma de describir y documentar un algoritmo (y un programa informático de uno). Al igual que el flujo de programa de una máquina Minsky, un diagrama de flujo siempre comienza en la parte superior de una página y continúa hacia abajo. Sus símbolos primarios son solo cuatro: la flecha dirigida que muestra el flujo del programa, el rectángulo (SECUENCIA, GOTO), el diamante (IF-THEN-ELSE) y el punto (O-tie). Las estructuras canónicas Böhm-Jacopini están hechas de estas formas primitivas. Las subestructuras pueden "anidar" en rectángulos, pero solo si se produce una única salida desde la superestructura. Los símbolos y su uso para construir las estructuras canónicas se muestran en el diagrama.
Ejemplos
Ejemplo de algoritmo
Uno de los algoritmos más simples es encontrar el número más grande en una lista de números de orden aleatorio. Encontrar la solución requiere mirar cada número en la lista. De esto sigue un algoritmo simple, que se puede establecer en una descripción de alto nivel de prosa en inglés, como:
Descripción de alto nivel:
- Si no hay números en el conjunto, entonces no hay un número más alto.
- Suponga que el primer número en el conjunto es el número más grande en el conjunto.
- Para cada número restante en el conjunto: si este número es mayor que el número mayor actual, considere este número como el número más grande en el conjunto.
- Cuando no quedan números en el conjunto para iterar, considere el número más grande actual como el número más grande del conjunto.
Descripción (cuasi-) formal: Escrito en prosa pero mucho más cerca del lenguaje de alto nivel de un programa de computadora, la siguiente es la codificación más formal del algoritmo en pseudocódigo o código pidgin:
Algorithm LargestNumber Entrada: Una lista de números L . Salida: El número más grande de la lista L .
Si L.size = 0 retorno nula grande ← L [0] para cada elemento en L , hacer si elemento > grande , entonces más grande ← elemento volver más grande
- "←" denota asignación. Por ejemplo, " artículo ← más grande " significa que el valor de mayor cambia al valor del artículo .
- " return " termina el algoritmo y emite el siguiente valor.
Algoritmo de Euclides
El algoritmo de Euclides para calcular el máximo divisor común (GCD) a dos números aparece como Proposición II en el Libro VII ("Teoría elemental del número") de sus Elementos . Euclides plantea el problema así: "Dado dos números no primos entre sí, para encontrar su mayor medida común". Él define "Un número [para ser] una multitud compuesta de unidades": un número de conteo, un número entero positivo que no incluye cero. Para "medir" es colocar una longitud de medición más corta s sucesivamente ( q veces) a lo largo de una longitud más larga l hasta que la porción restante r sea menor que la longitud más corta s . En palabras modernas, , siendo q el cociente, o el resto r es el "módulo", la parte entero-fraccional que queda después de la división.
Para que el método de Euclides tenga éxito, las longitudes iniciales deben cumplir dos requisitos: (i) las longitudes no deben ser cero, Y (ii) la resta debe ser "adecuada"; es decir, una prueba debe garantizar que el menor de los dos números se sustrae del más grande (alternativamente, los dos pueden ser iguales, por lo que su resta arroja cero).
La prueba original de Euclides agrega un tercer requisito: las dos longitudes no deben ser primarias entre sí. Euclides estipuló esto para que pudiera construir una prueba reductio ad absurdum de que la medida común de los dos números es de hecho la más grande . Si bien el algoritmo de Nicomachus es el mismo que el de Euclides, cuando los números son primos entre sí, arroja el número "1" para su medida común. Entonces, para ser precisos, el siguiente es realmente el algoritmo de Nicomachus.
Lenguaje de programación para el algoritmo de Euclides
Solo se requieren unos pocos tipos deinstrucción para ejecutar el algoritmo de Euclides: algunas pruebas lógicas (GOTO condicional), GOTO incondicional, asignación (reemplazo) y resta.
- Una ubicación está simbolizada por letras mayúsculas, por ejemplo, S, A, etc.
- La cantidad variable (número) en una ubicación está escrita en letras minúsculas y (generalmente) asociada con el nombre de la ubicación. Por ejemplo, la ubicación L al comienzo podría contener el número l = 3009.
Un programa poco elegante para el algoritmo de Euclides
El siguiente algoritmo se enmarca como la versión de cuatro pasos de Knuth de Euclides y Nicomachus, pero en lugar de usar la división para hallar el resto, usa sustracciones sucesivas de la longitud más corta s de la longitud restante r hasta que r es menor que s . La descripción de alto nivel, mostrada en negrita, es una adaptación de Knuth 1973: 2-4:
ENTRADA :
1 [en dos ubicaciones L y S poner los números l y s que representan las dos longitudes]: ENTRADA L, S 2 [Inicializar R: haga que la longitud restante r sea igual a la longitud de inicio / inicial / entrada l ]: R ← L
E0: [Asegurar r ≥ s ]
3 [Asegúrese de que el menor de los dos números esté en S y el más grande en R]: SI R> S ENTONCES el contenido de L es el número más grande así que omita los pasos de intercambio 4, 5 y 6: GOTO paso 6 MÁS intercambia los contenidos de R y S. 4 L ← R (este primer paso es redundante, pero es útil para una discusión posterior). 5 R ← S 6 S ← L
E1: [Encontrar resto] : Hasta que la longitud restante r en R sea menor que la menor longitud s en S, restar repetidamente el número de medición s en S de la longitud restante r en R.
7 SI S> R LUEGO hecho midiendo tan GOTO 10 MÁS medir de nuevo, 8 R ← R - S 9 [Lazo restante]: GOTO 7.
E2: [¿El resto es cero?] : O BIEN (i) la última medida fue exacta, el resto en R es cero, y el programa puede detenerse, O (ii) el algoritmo debe continuar: la última medida dejó un resto en R menos que la medición del número en S.
10 SI R = 0 ENTONCES hecho GOTO paso 15 MÁS CONTINÚE CON el paso 11,
E3: [Intercambio s y r ] : La tuerca de algoritmo de Euclides. Use el resto r para medir lo que antes era un número menor s ; L sirve como una ubicación temporal.
11 L ← R 12 R ← S 13 S ← L 14 [Repita el proceso de medición]: GOTO 7
SALIDA :
15 [Hecho. S contiene el mayor divisor común]: IMPRESIÓN S
HECHO :
16 HALT, END, STOP.
Un programa elegante para el algoritmo de Euclides
La siguiente versión del algoritmo de Euclides requiere solo seis instrucciones básicas para hacer lo que trece deben hacer con "Inelegante"; peor, "Inelegante" requiere más tipos de instrucciones. El diagrama de flujo de "Elegante" se puede encontrar en la parte superior de este artículo. En el lenguaje Básico (no estructurado), los pasos están numerados, y la instrucción es la instrucción de asignación simbolizada por ←.
LET [] = []5 REM Algoritmo de Euclides para el máximo divisor común
6 IMPRESIÓN "Escriba dos enteros mayores que 0"
10 ENTRADA A , B
20 SI B = 0 LUEGO GOTO 80
30 SI A > B LUEGO GOTO 60
40 LET B = B - A
50 GOTO 20
60 DEJAR A = A - B
70 GOTO 20
80 IMPRIMIR A
90 END
La siguiente versión se puede utilizar con lenguajes orientados a objetos:
// Algoritmo de Euclides para el mayor divisor común
entero euclidAlgorithm ( int A , int B ) {
A = Math . abs ( A );
B = Matemáticas . abs ( B );
while ( B ! = 0 ) {
if ( A > B ) A = A - B ;
si no B = B - A ;
}
return A;
}
Cómo funciona "Elegante" : en lugar de un "bucle Euclid" externo, "Elegante" se desplaza hacia adelante y hacia atrás entre dos "bucles", un bucle A> B que calcula A ← A - B y un B ≤ A bucle que calcula B ← B - A. Esto funciona porque, cuando por fin el minuendo M es menor o igual que el sustraendo S (Diferencia = Minuendo - Subtrayendo), el minuendo puede convertirse en s (la nueva longitud de medición) y el substraendo puede convertirse en la nueva r (la longitud a medir); en otras palabras, el "sentido" de la resta se invierte.
Probando los algoritmos de Euclid
¿Un algoritmo hace lo que su autor quiere que haga? Algunos casos de prueba suelen ser suficientes para confirmar la funcionalidad principal. Una fuente usa 3009 y 884. Knuth sugirió 40902, 24140. Otro caso interesante son los dos números primos relativamente 14157 y 5950.
Pero los casos excepcionales deben ser identificados y probados. ¿Funcionará "Inelegant" correctamente cuando R> S, S> R, R = S? Ídem para "Elegante": B> A, A> B, A = B? (Sí a todo). ¿Qué sucede cuando un número es cero, ambos números son cero? ("Inelegante" computa para siempre en todos los casos; "Elegante" computa para siempre cuando A = 0.) ¿Qué sucede si se ingresan números negativos ? Números fraccionarios? Si los números de entrada, es decir, el dominio de la función calculada por el algoritmo / programa, deben incluir solo enteros positivos, incluido cero, entonces las fallas en cero indican que el algoritmo (y el programa que lo ejemplifica) es una función parcial en lugar de una función total. Una falla notable debido a las excepciones es la falla del cohete Ariane 5 Flight 501 (4 de junio de 1996).
Prueba de corrección del programa mediante el uso de la inducción matemática : Knuth demuestra la aplicación de la inducción matemática a una versión "extendida" del algoritmo de Euclides, y propone "un método general aplicable para probar la validez de cualquier algoritmo". Tausworthe propone que una medida de la complejidad de un programa sea la longitud de su prueba de corrección.
Midiendo y mejorando los algoritmos de Euclid
Elegancia (compacidad) versus bondad (velocidad) : con solo seis instrucciones básicas, "Elegante" es el claro ganador, en comparación con "Inelegante" en trece instrucciones. Sin embargo, "Inelegant" es más rápido (llega a HALT en menos pasos). El análisis de algoritmo indica por qué este es el caso: "Elegante" hace dos pruebas condicionales en cada bucle de resta, mientras que "Inelegante" solo hace una. Como el algoritmo (normalmente) requiere muchos bucles, en promedio se desperdicia mucho tiempo haciendo un "B = 0". prueba que se necesita solo después de calcular el resto.
¿Se pueden mejorar los algoritmos? : Una vez que el programador juzga que un programa es "adecuado" y "efectivo", es decir, computa la función prevista por su autor, entonces la pregunta es: ¿se puede mejorar?
La compacidad de "Inelegant" puede mejorarse mediante la eliminación de cinco pasos. Pero Chaitin demostró que la compactación de un algoritmo no puede automatizarse mediante un algoritmo generalizado; más bien, solo puede hacerse heurísticamente; es decir, mediante búsqueda exhaustiva (ejemplos que se encuentran en Busy castor), prueba y error, inteligencia, perspicacia, aplicación del razonamiento inductivo, etc. Observe que los pasos 4, 5 y 6 se repiten en los pasos 11, 12 y 13. Comparación con "Elegante" proporciona una pista de que estos pasos, junto con los pasos 2 y 3, se pueden eliminar. Esto reduce el número de instrucciones básicas de trece a ocho, lo que lo hace "más elegante" que "Elegante", en nueve pasos.
La velocidad de "Elegante" se puede mejorar moviendo el "B = 0?" prueba fuera de los dos bucles de resta. Este cambio requiere la adición de tres instrucciones (B = 0 ?, A = 0 ?, GOTO). Ahora "Elegante" calcula los números de ejemplo más rápido; si este es siempre el caso para cualquier A, B y R dado, S requeriría un análisis detallado.
Análisis algorítmico
Con frecuencia es importante saber qué cantidad de un recurso en particular (como el tiempo o el almacenamiento) se requiere teóricamente para un algoritmo dado. Se han desarrollado métodos para el análisis de algoritmos para obtener tales respuestas cuantitativas (estimaciones); por ejemplo, el algoritmo de clasificación anterior tiene un requisito de tiempo de O ( n ), usando la notación O grande con n como la longitud de la lista. En todo momento, el algoritmo solo necesita recordar dos valores: el número más grande encontrado hasta el momento y su posición actual en la lista de entrada. Por lo tanto, se dice que tiene un requisito de espacio de O (1) , si el espacio requerido para almacenar los números ingresados no se cuenta, o O ( n ) si se cuenta.
Diferentes algoritmos pueden completar la misma tarea con un conjunto diferente de instrucciones en menos o más tiempo, espacio o 'esfuerzo' que otros. Por ejemplo, un algoritmo de búsqueda binario (con costo O (log n)) supera una búsqueda secuencial (costo O (n)) cuando se usa para búsquedas de tabla en listas ordenadas o matrices.
Formal versus empírico
El análisis y el estudio de los algoritmos es una disciplina de la informática y, a menudo, se practica de forma abstracta sin el uso de un lenguaje de programación o implementación específicos. En este sentido, el análisis de algoritmo se asemeja a otras disciplinas matemáticas porque se centra en las propiedades subyacentes del algoritmo y no en los detalles de una implementación en particular. Por lo general, el pseudocódigo se usa para el análisis ya que es la representación más simple y general. Sin embargo, en última instancia, la mayoría de los algoritmos generalmente se implementan en plataformas de hardware / software particulares y su eficiencia algorítmica se pone a prueba con el uso de código real. Para la solución de un problema "único", la eficiencia de un algoritmo particular puede no tener consecuencias significativas (a menos que n sea extremadamente grande) pero para los algoritmos diseñados para un uso científico rápido interactivo, comercial o de larga duración puede ser crítico. Escalar desde n pequeño a n grande frecuentemente expone algoritmos ineficientes que de otra manera serían benignos.
Las pruebas empíricas son útiles porque pueden descubrir interacciones inesperadas que afectan el rendimiento. Los puntos de referencia se pueden usar para comparar posibles mejoras antes / después de un algoritmo después de la optimización del programa. Sin embargo, las pruebas empíricas no pueden reemplazar el análisis formal y no son triviales para realizar de manera justa.
Eficiencia de ejecución
Para ilustrar las posibles mejoras posibles incluso en algoritmos bien establecidos, una innovación significativa reciente, relacionada con los algoritmos FFT (utilizados en gran medida en el campo del procesamiento de imágenes), puede reducir el tiempo de procesamiento hasta 1,000 veces para aplicaciones como imágenes médicas. En general, las mejoras de velocidad dependen de las propiedades especiales del problema, que son muy comunes en las aplicaciones prácticas. Las aceleraciones de esta magnitud permiten que los dispositivos informáticos que hacen un uso extensivo del procesamiento de imágenes (como cámaras digitales y equipos médicos) consuman menos energía.
Clasificación
Hay varias formas de clasificar algoritmos, cada uno con sus propios méritos.
Por implementación
Una forma de clasificar los algoritmos es por medios de implementación.
- Recursión
- Un algoritmo recursivo es uno que invoca (hace referencia) a sí mismo repetidamente hasta que una determinada condición (también conocida como condición de terminación) coincide, que es un método común para la programación funcional. Los algoritmos iterativos usan construcciones repetitivas como bucles y, a veces, estructuras de datos adicionales como pilas para resolver los problemas dados. Algunos problemas son naturalmente adecuados para una implementación u otra. Por ejemplo, las torres de Hanoi se comprenden bien utilizando la implementación recursiva. Cada versión recursiva tiene una versión iterativa equivalente (pero posiblemente más o menos compleja), y viceversa.
- Lógico
- Un algoritmo puede verse como una deducción lógica controlada. Esta noción puede expresarse como: Algoritmo = lógica + control . El componente lógico expresa los axiomas que pueden usarse en el cálculo y el componente de control determina la forma en que se aplica la deducción a los axiomas. Esta es la base del paradigma de programación lógica. En los lenguajes de programación de lógica pura, el componente de control es fijo y los algoritmos se especifican suministrando solo el componente lógico. El atractivo de este enfoque es la semántica elegante: un cambio en los axiomas tiene un cambio bien definido en el algoritmo.
- En serie, paralelo o distribuido
- Los algoritmos generalmente se discuten con la suposición de que las computadoras ejecutan una instrucción de un algoritmo a la vez. Esas computadoras a veces se llaman computadoras seriales. Un algoritmo diseñado para dicho entorno se denomina algoritmo en serie, a diferencia de los algoritmos paralelos o los algoritmos distribuidos. Los algoritmos paralelos aprovechan arquitecturas de computadora donde varios procesadores pueden trabajar en un problema al mismo tiempo, mientras que los algoritmos distribuidos utilizan múltiples máquinas conectadas a una red informática. Los algoritmos paralelos o distribuidos dividen el problema en subproblemas más simétricos o asimétricos y reúnen los resultados nuevamente. El consumo de recursos en tales algoritmos no es solo ciclos de procesador en cada procesador sino también la sobrecarga de comunicación entre los procesadores. Algunos algoritmos de clasificación se pueden paralelizar de manera eficiente, pero su sobrecarga de comunicación es costosa. Los algoritmos iterativos son generalmente paralelizables. Algunos problemas no tienen algoritmos paralelos y se denominan problemas de serie inherentes.
- Determinista o no determinista
- Los algoritmos deterministas resuelven el problema con una decisión exacta en cada paso del algoritmo, mientras que los algoritmos no deterministas resuelven los problemas mediante la adivinación, aunque las conjeturas típicas se vuelven más precisas mediante el uso de la heurística.
- Exacto o aproximado
- Mientras que muchos algoritmos alcanzan una solución exacta, los algoritmos de aproximación buscan una aproximación más cercana a la verdadera solución. La aproximación se puede alcanzar utilizando una estrategia determinista o aleatoria. Tales algoritmos tienen un valor práctico para muchos problemas difíciles. Uno de los ejemplos de un algoritmo aproximado es el problema de Knapsack. El problema de Knapsack es un problema donde hay un conjunto de elementos determinados. El objetivo del problema es empacar la mochila para obtener el valor total máximo. Cada artículo tiene algún peso y algún valor. El peso total que podemos transportar no es más que un número fijo X. Por lo tanto, debemos considerar el peso de los artículos así como su valor.
- Algoritmo cuántico
- Funcionan con un modelo realista de computación cuántica. El término se usa generalmente para aquellos algoritmos que parecen intrínsecamente cuánticos o que utilizan alguna característica esencial de la computación cuántica, como la superposición cuántica o el enredo cuántico.
Por paradigma de diseño
Otra forma de clasificar los algoritmos es mediante su metodología de diseño o paradigma. Hay una cierta cantidad de paradigmas, cada uno diferente del otro. Además, cada una de estas categorías incluye muchos tipos diferentes de algoritmos. Algunos paradigmas comunes son:
- Fuerza bruta o búsqueda exhaustiva
- Este es el método ingenuo de probar todas las soluciones posibles para ver cuál es el mejor.
- Divide y conquistaras
- Un algoritmo de dividir y conquistar reduce repetidamente una instancia de un problema a una o más instancias más pequeñas del mismo problema (generalmente recursivamente) hasta que las instancias sean lo suficientemente pequeñas como para resolverlas fácilmente. Uno de esos ejemplos de divide y vencerás es la clasificación por fusión. La ordenación se puede hacer en cada segmento de datos después de dividir los datos en segmentos y la ordenación de datos completos se puede obtener en la fase de conquista fusionando los segmentos. Una variante más simple de divide y vencerás se llama algoritmo de disminución y conquista, que resuelve un subproblema idéntico y utiliza la solución de este subproblema para resolver el problema más grande. Dividir y vencer divide el problema en múltiples subproblemas y, por lo tanto, la etapa de conquista es más compleja que los algoritmos de disminución y conquista. Un ejemplo de algoritmo de disminución y conquista es el algoritmo de búsqueda binaria.
- Búsqueda y enumeración
- Muchos problemas (como jugar al ajedrez) se pueden modelar como problemas en los gráficos. Un algoritmo de exploración de gráficos especifica reglas para moverse por un gráfico y es útil para tales problemas. Esta categoría también incluye algoritmos de búsqueda, enumeración de ramas y límites y retroceso.
- Algoritmo aleatorizado
- Tales algoritmos hacen algunas elecciones al azar (o pseudoaleatoriamente). Pueden ser muy útiles para encontrar soluciones aproximadas para problemas donde encontrar soluciones exactas puede ser poco práctico (ver el método heurístico a continuación). Para algunos de estos problemas, se sabe que las aproximaciones más rápidas deben implicar algo de aleatoriedad. Si los algoritmos aleatorios con complejidad de tiempo polinomial pueden ser los algoritmos más rápidos para algunos problemas es una pregunta abierta conocida como el problema P versus NP. Hay dos clases grandes de tales algoritmos:
- Los algoritmos de Monte Carlo devuelven una respuesta correcta con alta probabilidad. Por ejemplo, RP es la subclase de estos que se ejecutan en tiempo polinomial.
- Los algoritmos de Las Vegas siempre devuelven la respuesta correcta, pero su tiempo de ejecución solo está limitado probabilísticamente, por ejemplo, ZPP.
- Reducción de la complejidad
- Esta técnica implica resolver un problema difícil transformándolo en un problema mejor conocido para el cual tenemos (con suerte) algoritmos asintóticamente óptimos. El objetivo es encontrar un algoritmo reductor cuya complejidad no esté dominada por los algoritmos reducidos resultantes. Por ejemplo, un algoritmo de selección para encontrar la mediana en una lista desordenada implica primero clasificar la lista (la parte costosa) y luego extraer el elemento medio en la lista ordenada (la parte barata). Esta técnica también se conoce como transformar y conquistar .
- Seguimiento posterior
- En este enfoque, las soluciones múltiples se crean incrementalmente y se abandonan cuando se determina que no pueden conducir a una solución completa válida.
Problemas de optimización
Para problemas de optimización hay una clasificación más específica de algoritmos; un algoritmo para tales problemas puede pertenecer a una o más de las categorías generales descritas anteriormente, así como a uno de los siguientes:
- Programación lineal
- Cuando se buscan soluciones óptimas para una función lineal ligada a restricciones lineales de igualdad y desigualdad, las restricciones del problema se pueden usar directamente para producir las soluciones óptimas. Existen algoritmos que pueden resolver cualquier problema en esta categoría, como el popular algoritmo simplex. Los problemas que se pueden resolver con programación lineal incluyen el problema de flujo máximo para gráficos dirigidos. Si un problema requiere además que una o más de las incógnitas debe ser un número entero, entonces se clasifica en una programación entera. Un algoritmo de programación lineal puede resolver dicho problema si se puede demostrar que todas las restricciones para valores enteros son superficiales, es decir, que las soluciones satisfacen estas restricciones de todos modos. En el caso general, se usa un algoritmo especializado o un algoritmo que encuentra soluciones aproximadas,
- Programación dinámica
- Cuando un problema muestra que las subestructuras óptimas -es decir, la solución óptima para un problema puede construirse desde soluciones óptimas a subproblemas- y subproblemas superpuestos, es decir, los mismos subproblemas se utilizan para resolver muchas instancias de problemas diferentes, un enfoque más rápido llamado programación dinámica evita volver a calcular las soluciones que ya se han calculado. Por ejemplo, el algoritmo de Floyd-Warshall, el camino más corto hacia un objetivo desde un vértice en un gráfico ponderado, se puede encontrar utilizando la ruta más corta hacia el objetivo desde todos los vértices adyacentes. La programación dinámica y la memorización van de la mano. La diferencia principal entre programación dinámica y división y conquista es que los subproblemas son más o menos independientes en división y conquista, mientras que los subproblemas se superponen en la programación dinámica. La diferencia entre la programación dinámica y la recursión directa es en el almacenamiento en caché o la memorización de llamadas recursivas. Cuando los subproblemas son independientes y no hay repetición, la memorización no ayuda; por lo tanto, la programación dinámica no es una solución para todos los problemas complejos. Al usar la memorización o mantener una tabla de subproblemas ya resueltos,
- El método codicioso
- Un algoritmo codicioso es similar a un algoritmo de programación dinámica en el sentido de que funciona mediante el examen de las subestructuras, en este caso no del problema sino de una solución dada. Tales algoritmos comienzan con alguna solución, que se puede dar o se ha construido de alguna manera, y mejorarla haciendo pequeñas modificaciones. Para algunos problemas, pueden encontrar la solución óptima, mientras que para otros se detienen en óptimas locales, es decir, en soluciones que el algoritmo no puede mejorar, pero que no son óptimas. El uso más popular de los algoritmos codiciosos es encontrar el árbol de expansión mínimo donde encontrar la solución óptima es posible con este método. Huffman Tree, Kruskal, Prim, Sollin son algoritmos codiciosos que pueden resolver este problema de optimización.
- El método heurístico
- En los problemas de optimización, los algoritmos heurísticos se pueden utilizar para encontrar una solución cercana a la solución óptima en los casos en que no es práctico encontrar la solución óptima. Estos algoritmos funcionan acercándose cada vez más a la solución óptima a medida que avanzan. En principio, si se ejecutan durante un tiempo infinito, encontrarán la solución óptima. Su mérito es que pueden encontrar una solución muy cercana a la solución óptima en un tiempo relativamente corto. Dichos algoritmos incluyen búsqueda local, búsqueda tabú, recocido simulado y algoritmos genéticos. Algunos de ellos, como el recocido simulado, son algoritmos no deterministas, mientras que otros, como la búsqueda tabú, son deterministas. Cuando se conoce un límite en el error de la solución no óptima, el algoritmo se categoriza además como un algoritmo de aproximación.
Por campo de estudio
Cada campo de la ciencia tiene sus propios problemas y necesita algoritmos eficientes. Los problemas relacionados en un campo a menudo se estudian juntos. Algunas clases de ejemplo son algoritmos de búsqueda, algoritmos de clasificación, algoritmos de fusión, algoritmos numéricos, algoritmos de gráficos, algoritmos de cadenas, algoritmos geométricos computacionales, algoritmos combinatorios, algoritmos médicos, aprendizaje automático, criptografía, algoritmos de compresión de datos y técnicas de análisis sintáctico.
Los campos tienden a superponerse entre sí, y los avances de algoritmo en un campo pueden mejorar los de otros campos, a veces completamente no relacionados. Por ejemplo, la programación dinámica se inventó para la optimización del consumo de recursos en la industria, pero ahora se usa para resolver una amplia gama de problemas en muchos campos.
Por complejidad
Los algoritmos se pueden clasificar por la cantidad de tiempo que necesitan completar en comparación con su tamaño de entrada:
- Tiempo constante: si el tiempo que necesita el algoritmo es el mismo, independientemente del tamaño de la entrada. Por ejemplo, un acceso a un elemento de matriz.
- Tiempo lineal: si el tiempo es proporcional al tamaño de entrada. Por ejemplo, el recorrido de una lista.
- Tiempo logarítmico: si el tiempo es una función logarítmica del tamaño de entrada. Ej. Algoritmo de búsqueda binaria.
- Tiempo polinomial: si el tiempo es una potencia del tamaño de entrada. Por ejemplo, el algoritmo de ordenación de burbujas tiene una complejidad de tiempo cuadrática.
- Tiempo exponencial: si el tiempo es una función exponencial del tamaño de entrada. Ej. Búsqueda de fuerza bruta.
Algunos problemas pueden tener múltiples algoritmos de diferente complejidad, mientras que otros problemas pueden no tener algoritmos o ningún algoritmo eficiente conocido. También hay asignaciones de algunos problemas a otros problemas. Debido a esto, se encontró que era más adecuado clasificar los problemas en sí mismos en lugar de los algoritmos en clases de equivalencia en función de la complejidad de los mejores algoritmos posibles para ellos.
Algoritmos continuos
El adjetivo "continuo" cuando se aplica a la palabra "algoritmo" puede significar:
- Algoritmo que opera en datos que representan cantidades continuas, aunque estos datos están representados por aproximaciones discretas; dichos algoritmos se estudian en análisis numérico; o
- Un algoritmo en forma de ecuación diferencial que opera continuamente en los datos, ejecutándose en una computadora analógica.
Asuntos legales
Los algoritmos, por sí mismos, generalmente no son patentables. En los Estados Unidos, un reclamo que consiste únicamente en manipulaciones simples de conceptos abstractos, números o señales no constituye "procesos" (USPTO 2006), y por lo tanto los algoritmos no son patentables (como en Gottschalk v. Benson). Sin embargo, las aplicaciones prácticas de algoritmos son a veces patentables. Por ejemplo, en Diamond v. Diehr, la aplicación de un algoritmo de retroalimentación simple para ayudar al curado del caucho sintético se consideró patentable. El patentamiento de software es muy controvertido, y hay patentes altamente criticadas que involucran algoritmos, especialmente algoritmos de compresión de datos, como la patente LZW de Unisys.
Además, algunos algoritmos criptográficos tienen restricciones de exportación (ver exportación de criptografía).
El investigador, Andrew Tutt, argumenta que los algoritmos deben ser supervisados por una agencia reguladora especializada, similar a la FDA. Su trabajo académico enfatiza que el surgimiento de algoritmos cada vez más complejos requiere la necesidad de pensar en los efectos de los algoritmos de hoy. Debido a la naturaleza y complejidad de los algoritmos, resultará difícil hacer que los algoritmos rindan cuentas bajo la ley penal. Tutt reconoce que, si bien algunos algoritmos serán beneficiosos para ayudar a satisfacer la demanda tecnológica, otros no deberían usarse ni venderse si no cumplen con los requisitos de seguridad. Por lo tanto, para Tutt, los algoritmos requerirán "formas más cercanas de uniformidad federal, juicio experto, independencia política y revisión previa al mercado para evitar la introducción de algoritmos inaceptablemente peligrosos en el mercado".
Historia: desarrollo de la noción de "algoritmo"
Antiguo Cercano Oriente
Algoritmos fueron utilizados en la antigua Grecia. Dos ejemplos son el Tamiz de Eratóstenes, que fue descrito en Introducción a la aritmética por Nicomachus, y el algoritmo euclidiano, que se describió por primera vez en Elementos de Euclides (300 AC). Las tabletas de arcilla babilónicas describen y emplean procedimientos algorítmicos para calcular el tiempo y el lugar de eventos astronómicos significativos.
Símbolos discretos y distinguibles
Marcas de conteo : para hacer un seguimiento de sus rebaños, sus sacos de grano y su dinero, los antiguos usaban el recuento: acumulaban piedras o marcas arañando palos, o haciendo símbolos discretos en arcilla. A través del uso de marcas y símbolos babilónicos y egipcios, eventualmente los números romanos y el ábaco evolucionaron (Dilson, p 16-41). Las marcas de conteo aparecen prominentemente en la aritmética de sistema numérico unario utilizada en la máquina de Turing y los cálculos de la máquina Post-Turing.
Manipulación de símbolos como "marcadores de posición" para números: álgebra
El trabajo de los antiguos geómetras griegos (algoritmo euclidiano), el matemático indio Brahmagupta y el matemático persa Al-Khwarizmi (de cuyo nombre se derivan los términos "algorismo" y "algoritmo") y matemáticos europeos occidentales culminaron en la noción de Leibniz de el racionador de cálculo (aprox. 1680):
Mecanismos mecánicos con estados discretos
El reloj: Bolter acredita la invención del reloj impulsado por peso como "La invención clave [de Europa en la Edad Media]", en particular el escape de borde que nos proporciona el tic y el tock de un reloj mecánico. "La máquina automática precisa" condujo inmediatamente a "autómatas mecánicos" comenzando en el siglo XIII y finalmente a "máquinas computacionales": el motor diferencial y los motores analíticos de Charles Babbage y la condesa Ada Lovelace, de mediados del siglo XIX. A Lovelace se le atribuye la primera creación de un algoritmo diseñado para procesar en una computadora: el motor analítico de Babbage, el primer dispositivo considerado una verdadera computadora completa de Turing en lugar de solo una calculadora, y a veces se lo denomina "el primer programador de la historia". a pesar de una implementación completa de Babbage '
Máquinas lógicas 1870-Stanley Jevons '' ábaco lógico '' y '' máquina lógica '' : El problema técnico era reducir las ecuaciones booleanas cuando se presentaban en una forma similar a lo que ahora se conoce como mapas de Karnaugh. Jevons (1880) describe primero un simple "ábaco" de "trozos de madera provistos de alfileres, ideados de modo que cualquier parte o clase de las combinaciones [lógicas] pueda ser elegida mecánicamente ... Más recientemente, sin embargo, he reducido el sistema a una forma completamente mecánica, y así han incorporado todo el proceso indirecto de inferencia en lo que se puede llamar una Máquina Lógica "Su máquina viene equipada con" ciertas barras de madera móviles "y" al pie hay 21 teclas como las de un piano " [etc] ... ". Con esta máquina podría analizar un "
Esta máquina la mostró en 1870 ante los Fellows de la Royal Society. Sin embargo, otro lógico, John Venn, en su Lógica simbólica de 1881 , dirigió una mirada amarga a este esfuerzo: "No tengo una gran estimación del interés o la importancia de lo que a veces se llaman máquinas lógicas ... no me parece que cualquier artilugio actualmente conocido o susceptible de ser descubierto realmente merece el nombre de máquinas lógicas "; ver más en caracterizaciones de Algoritmo. Pero para no quedarse atrás, él también presentó "un plan algo análogo, aprendo, al ábaco del Prof. Jevon ... [Y] [a] ganancia, que corresponde a la máquina lógica del Prof. Jevons, se puede describir el siguiente artilugio. Prefiero llamarlo simplemente una máquina de diagrama lógico ... pero supongo que podría hacer muy completamente todo lo que se puede esperar racionalmente de cualquier máquina lógica ".
Telar jacquard, tarjetas perforadas Hollerith, telegrafía y telefonía: el relevo electromecánico : Bell y Newell (1971) indican que el telar Jacquard (1801), el precursor de las tarjetas Hollerith (tarjetas perforadas, 1887) y las "tecnologías de conmutación telefónica" fueron las raíces de un árbol que conduce al desarrollo de las primeras computadoras. A mediados del siglo XIX, el telégrafo, el precursor del teléfono, se usaba en todo el mundo; su codificación discreta y distinguible de letras como "puntos y rayas" era un sonido común. A fines del siglo XIX, se usaba la cinta de teletipo (alrededor de 1870), al igual que el uso de las cartas de Hollerith en el censo de Estados Unidos de 1890. Luego vino la teleimpresora (alrededor de 1910) con el uso del código de Baudot en cinta adhesiva.
Las redes de conmutación de teléfonos de relés electromecánicos (inventadas en 1835) estaban detrás del trabajo de George Stibitz (1937), el inventor del dispositivo de adición digital. Mientras trabajaba en los Laboratorios Bell, observó el uso "oneroso" de las calculadoras mecánicas con engranajes ". Se fue a su casa una tarde de 1937 con la intención de poner a prueba su idea ... Cuando terminó el juego, Stibitz había construido un dispositivo binario" .
Davis (2000) observa la importancia particular del relé electromecánico (con sus dos "estados binarios" abiertos y cerrados ):
- Fue solo con el desarrollo, a partir de la década de 1930, de las calculadoras electromecánicas que utilizan relés eléctricos, que las máquinas se construyeron teniendo el alcance que Babbage había previsto ".
Matemáticas durante el siglo XIX hasta mediados del siglo XX
Símbolos y reglas : en rápida sucesión, las matemáticas de George Boole (1847, 1854), Gottlob Frege (1879) y Giuseppe Peano (1888-1889) redujeron la aritmética a una secuencia de símbolos manipulados por reglas. Los principios de la aritmética de Peano , presentados por un nuevo método (1888) fue "el primer intento de una axiomatización de las matemáticas en un lenguaje simbólico".
Pero Heijenoort le da a Frege (1879) este prestigio: el de Frege es "tal vez la obra individual más importante jamás escrita en lógica ... en la que vemos un 'lenguaje de fórmula', que es una lengua tradicional , un lenguaje escrito con símbolos especiales , "por pensamiento puro", es decir, libre de adornos retóricos ... construidos a partir de símbolos específicos manipulados según reglas definidas. "El trabajo de Frege fue simplificado y ampliado aún más por Alfred North Whitehead y Bertrand Russell en sus Principia Mathematica (1910-1913).
Las paradojas : al mismo tiempo aparecieron en la literatura varias paradojas perturbadoras, en particular la paradoja de Burali-Forti (1897), la paradoja de Russell (1902-03) y la paradoja de Richard. Las consideraciones resultantes llevaron al artículo de Kurt Gödel (1931) -se refiere específicamente a la paradoja del mentiroso- que reduce por completo las reglas de recursión a los números.
Efectividad de cálculo: En un esfuerzo por resolver el Entscheidungsproblem definido con precisión por Hilbert en 1928, los matemáticos primero se pusieron a definir lo que significaba un "método efectivo" o "cálculo efectivo" o "calculabilidad efectiva" (es decir, un cálculo que tendría éxito). En rápida sucesión, aparecieron los siguientes: Alonzo Church, Stephen Kleene y JB Rosser's λ-calculus una definición finamente perfeccionada de "recursión general" de la obra de Gödel que actúa según las sugerencias de Jacques Herbrand (cf. Gödel's Princeton lectures of 1934) y simplificaciones posteriores por Kleene. La prueba de la Iglesia de que el Entscheidungsproblem no tenía solución, Emil Post ' s definición de calculabilidad efectiva como un trabajador que sigue sin cuidado una lista de instrucciones para moverse hacia la izquierda o la derecha a través de una secuencia de habitaciones y mientras marca o borra un papel u observa el papel y toma una decisión de sí o no sobre la siguiente instrucción. La prueba de Alan Turing de que el Entscheidungsproblem era irresoluble por el uso de su "máquina- [automática-]" -en efecto casi idéntica a la "formulación" de Post, la definición de J. Barkley Rosser de "método efectivo" en términos de "una máquina" . La propuesta de SC Kleene de un precursor de la "tesis de la Iglesia" a la que llamó "Tesis I", y unos años más tarde Kleene renombró su Tesis "Tesis de la Iglesia" y propuso la "Tesis de Turing".
Emil Post (1936) y Alan Turing (1936-37, 1939)
Aquí hay una notable coincidencia de dos hombres que no se conocen entre sí pero que describen un proceso de hombres-como-computadoras que trabajan en cómputos-y producen definiciones prácticamente idénticas.
Emil Post (1936) describió las acciones de una "computadora" (ser humano) de la siguiente manera:
- "... se trata de dos conceptos: el de un espacio de símbolos en el que debe llevarse a cabo el trabajo que conduce del problema a la respuesta, y un conjunto de indicaciones fijas e inalterables .
Su espacio de símbolos sería
- "una secuencia bidireccional infinita de espacios o cajas ... El solucionador de problemas o trabajador es moverse y trabajar en este espacio de símbolos, siendo capaz de estar dentro, y operar en un solo cuadro a la vez ... una caja es admitir solo dos condiciones posibles, es decir, estar vacío o sin marcar, y tener una sola marca en él, digamos un trazo vertical.
- "Una caja debe ser señalada y llamada el punto de partida ... un problema específico debe darse en forma simbólica por un número finito de cuadros [es decir, ENTRADA] marcados con un trazo. Asimismo la respuesta [es decir, OUTPUT] debe darse en forma simbólica mediante dicha configuración de cuadros marcados ....
- "Un conjunto de instrucciones aplicables a un problema general establece un proceso determinista cuando se aplica a cada problema específico. Este proceso termina solo cuando se trata de la dirección del tipo (C) [es decir, STOP]". Ver más en la máquina Post-Turing
El trabajo de Alan Turing precedió al de Stibitz (1937); se desconoce si Stibitz conocía el trabajo de Turing. El biógrafo de Turing creía que el uso de Turing de una máquina de escribir se derivaba de un interés juvenil: "Alan había soñado con inventar máquinas de escribir cuando era niño, la Sra. Turing tenía una máquina de escribir, y bien podría haber empezado preguntándose qué quería decir llamando una máquina de escribir 'mecánica' ". Dada la prevalencia del código Morse y la telegrafía, las máquinas de cinta de teletipo y los teletipos, podríamos conjeturar que todas eran influencias.
Turing -su modelo de computación ahora se llama máquina de Turing- comienza, al igual que Post, con un análisis de una computadora humana que reduce a un simple conjunto de movimientos básicos y "estados mentales". Pero continúa un paso más allá y crea una máquina como modelo de cómputo de números.
- "La computación normalmente se hace escribiendo ciertos símbolos en un papel. Podemos suponer que este trabajo está dividido en cuadrados como el libro aritmético de un niño ... Supongo entonces que el cálculo se lleva a cabo en papel unidimensional, es decir, en una cinta dividida en cuadrados. También supondré que el número de símbolos que pueden imprimirse es finito ...
- "El comportamiento de la computadora en cualquier momento está determinado por los símbolos que está observando y su" estado de ánimo "en ese momento. Podemos suponer que hay una B vinculada al número de símbolos o cuadrados que la computadora puede observe en un momento. Si desea observar más, debe usar observaciones sucesivas. También supondremos que el número de estados mentales que deben tenerse en cuenta es finito ...
- "Imaginemos que las operaciones realizadas por la computadora se dividen en 'operaciones simples' que son tan elementales que no es fácil imaginarlas divididas aún más".
La reducción de Turing produce lo siguiente:
- "Las operaciones simples deben, por lo tanto, incluir:
- "(a) Cambios del símbolo en uno de los cuadrados observados
- "(b) Cambios de uno de los cuadrados observados a otro cuadrado dentro de L cuadrados de uno de los cuadrados observados previamente.
"Puede ser que algunos de estos cambios invoquen necesariamente un cambio de estado mental. Por lo tanto, la operación más general debe considerarse como una de las siguientes:
-
- "(A) Un posible cambio (a) de símbolo junto con un posible cambio de estado mental.
- "(B) Un posible cambio (b) de cuadrados observados, junto con un posible cambio de estado mental"
- "Ahora podemos construir una máquina para hacer el trabajo de esta computadora".
Unos años más tarde, Turing amplió su análisis (tesis, definición) con esta expresión contundente:
- "Se dice que una función es" efectivamente calculable "si sus valores se pueden encontrar mediante algún proceso puramente mecánico. Aunque es bastante fácil obtener una comprensión intuitiva de esta idea, no obstante, es deseable tener una definición matemática expresable más definida ... [discute la historia de la definición, tal como se presentó arriba con respecto a Gödel, Herbrand, Kleene, Church, Turing y Post] ... Podemos tomar esta declaración literalmente, entendiendo por un proceso puramente mecánico uno que podría ser llevado a cabo por una máquina. Es posible dar una descripción matemática, en una cierta forma normal, de las estructuras de estas máquinas. El desarrollo de estas ideas conduce a la definición del autor de una función computable, y a una identificación de computabilidad † con una calculabilidad efectiva ....
- "† Usaremos la expresión" función computable "para referirnos a una función calculable por una máquina, y dejamos que" efectivamente calculable "se refiera a la idea intuitiva sin identificación particular con ninguna de estas definiciones".
JB Rosser (1939) y SC Kleene (1943)
J. Barkley Rosser definió un "método [matemático] efectivo" de la siguiente manera (cursiva añadida):
- El "método eficaz" se utiliza aquí en el sentido más bien especial de un método, cada paso del cual se determina con precisión y que seguramente producirá la respuesta en un número finito de pasos. Con este significado especial, se han dado tres definiciones precisas diferentes. hasta la fecha [su nota al pie n. ° 5, vea la discusión inmediatamente debajo]. El más simple de estos para decir (debido a Post y Turing) dice esencialmente que existe un método efectivo para resolver ciertos conjuntos de problemas si uno puede construir una máquina que luego resolver cualquier problema del conjunto sin intervención humana más allá de insertar la pregunta y (más tarde) leer la respuesta. Las tres definiciones son equivalentes, por lo que no importa cuál se use. Además, el hecho de que los tres sean equivalentes es un argumento muy fuerte para la corrección de cualquiera ". (Rosser 1939: 225-6)
La nota a pie de página número 5 de Rosser hace referencia al trabajo de (1) Church y Kleene y su definición de λ-definibilidad, en particular, el uso de Church en su An soluble Issol of Elementary Number Theory (1936); (2) Herbrand y Gödel y su uso de la recursividad, en particular el uso de Gödel en su famoso artículo Sobre proposiciones formalmente indecidibles de Principia Mathematica and Related Systems I (1931); y (3) Post (1936) y Turing (1936-37) en sus modelos de mecanismo de computación.
Stephen C. Kleene definió su ahora famosa "Tesis I" conocida como la tesis de Church-Turing. Pero lo hizo en el siguiente contexto (en negrita en el original):
- "12. Teorías algorítmicas ... Al establecer una teoría algorítmica completa, lo que hacemos es describir un procedimiento, realizable para cada conjunto de valores de las variables independientes, cuyo procedimiento termina necesariamente y de tal manera que a partir del resultado podemos lea una respuesta definitiva, "sí" o "no", a la pregunta "¿es verdad el valor predicado?" "(Kleene 1943: 273)
Historia después de 1950
Una serie de esfuerzos se han dirigido hacia un mayor refinamiento de la definición de "algoritmo", y la actividad está en curso debido a cuestiones que rodean, en particular, los fundamentos de las matemáticas (especialmente la tesis Church-Turing) y la filosofía de la mente (especialmente argumentos sobre inteligencia artificial). Para más, vea caracterizaciones de Algoritmo.